
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перед выполнением данной работы необходимо изучить содержимое пункта “Целочисленная арифметика”.
|
|
Лабораторная работа №4
Целочисленная арифметика
Перед выполнением данной работы необходимо изучить содержимое пункта “Целочисленная арифметика”.
Обратите внимание: В данной работе не разрешается использовать числа, представленные как строки символов.
1. Дано натуральное число. Найти сумму первой и последней цифры этого числа.
2. Дано натуральное число  . Переставить местами первую и последнюю цифры этого числа.
. Переставить местами первую и последнюю цифры этого числа.
3. Даны два натуральных числа 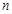 и
и 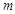 (
(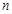 < 9999,
< 9999, 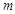 < 9999). Проверить, есть ли в записи числа
< 9999). Проверить, есть ли в записи числа 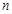 цифры, совпадающие с цифрами в записи числа
цифры, совпадающие с цифрами в записи числа 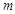 .
.
4. Дано натуральное число 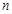 . Проверить, есть ли в записи числа три одинаковые цифры (
. Проверить, есть ли в записи числа три одинаковые цифры (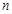 < 9999).
< 9999).
5. Дано натуральное число 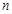 < 99. Дописать к нему цифру
< 99. Дописать к нему цифру 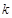 в конец и в начало.
в конец и в начало.
6. Среди всех 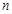 -значных чисел указать те, сумма цифр которых равна данному числу
-значных чисел указать те, сумма цифр которых равна данному числу 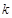 .
.
7. Найти наибольшую и наименьшую цифры в записи данного натурального числа.
8. Найти на отрезке 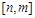 натуральное число, имеющее наибольшее количество делителей.
натуральное число, имеющее наибольшее количество делителей.
9. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N-1, у которых сумма всех цифр совпадает с суммой цифр данного числа. Пример. N = 44. Числа: 17, 26, 35.
10. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N-1, у которых произведение всех цифр совпадает с суммой цифр данного числа. Пример. N = 44. Числа: 18, 24.
11. Дано натуральное число N. Найти наибольшее число М (М> 1), на которое сумма цифр в цифровой записи числа N делится без остатка. Пример. N=12 345, М= 5. Сумма цифр числа N, равная 15, делится на 5.
12. Дано натуральное число N. Найти наименьшее число М (N< M< 2N), которое делится на сумму цифр числа N (без остатка). Пример. N = 12 345, М = 12 360. Число 12 360 делится на число 15 - сумму цифр числа N.
13. Дано натуральное число N (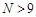 ). Определить количество нулей, идущих подряд в младших разрядах данного числа. Пример. N = 1 020 000. Количество нулей равно четырем.
). Определить количество нулей, идущих подряд в младших разрядах данного числа. Пример. N = 1 020 000. Количество нулей равно четырем.
14. Дано натуральное число N (N> 9). Определить количество нулей в цифровой записи числа, кроме нулей в младших разрядах. Пример. N=10 025 000. Количество нулей равно двум.
15. Дано натуральное число N (N > 9). Определить сумму цифр в первой половине числа (старшие разряды). Если число содержит нечетное количество цифр, “среднюю” цифру отнести к старшим разрядам. Пример. N = 1 234 567. Сумма составляет 1+2 + 3 + 4 = 10.
16. Дано натуральное число N(N> 9). Определить сумму цифр во второй половине числа (младшие разряды). Если число содержит нечетное количество цифр, “среднюю” цифру отнести к старшим разрядам. Пример. N= 1 234 567. Сумма составляет 5 + 6 + 7 = 18.
17. Дано натуральное число N. Если число содержит 3 цифры, то получить новое число М, которое образуется путем перестановки первой и последней цифр данного числа. Если количество цифр не 3, то М= N. Пример. N= 123, М= 321.
18. Дано натуральное число N. Если число содержит 5 цифр, то получить новое число М, которое образуется путем исключения средней цифры исходного числа. Если количество цифр не 5, то М = N. Пример. N= 12345, М= 1245.
19. Дано натуральное число п. Проверить, будут ли все цифры числа различными.
20. Дано натуральное число п. Поменять порядок следования цифр в этом числе на обратный.
21. Найти все делители натурального числа п.
22. Натуральное число М называется совершенным, если оно равно сумме всех своих делителей, включая 1, но исключая себя. Напечатать все совершенные числа меньшие заданного числа N.
23. Даны натуральные числа п, т. Найти все натуральные числа меньшие п, квадрат суммы цифр которых равен т.
24. На отрезке [2, п ] определить число с максимальной суммой делителей.
25. Дано натуральное число N. Определить количество цифр в цифровой записи данного числа, которые имеют наименьшее значение. Пример. N= 4548. Количество цифр с наименьшим значением равно двум (две цифры 4).
26. Дано натуральное число N. Определить количество цифр в цифровой записи данного числа, которые имеют наибольшее значение. Пример. N= 1808. Количество цифр с наибольшим значением равно двум (две цифры 8).
27. Дано натуральное число N. Получить новое число М, которое образуется из числа N путем замены последней цифры на значение наименьшей цифры в записи числа N. Пример. N= 128 452, М= 129 451.
28. Дано натуральное число N. Получить новое число М, которое образуется из числа N путем замены последней цифры на значение наибольшей цифры в записи числа N. Пример. N= 128 452, М= 128 458.
29. Определить количество М -значных натуральных чисел, у которых сумма цифр, стоящих в нечетных разрядах, равна N (1< N 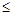 30, 0< M < 5).
30, 0< M < 5).
30. Дано натуральное число N. Выяснить, является ли данное число палиндромом. (Палиндром – симметричное число, например: 3, 22, 323, 12344321).