Екатеринбург

Сибирского государственного университета телекоммуникаций и информатики

(УрТИСИ СибГУТИ)

Факультет сокращенной подготовки (ФСП)

Контрольная работа № 1

по дисциплине «Теория электрических цепей»

Вариант № 13

Исполнитель: студент 1-го курса з/о

Группы №

Екатеринбург

2004г.

Задача №1.

Исходные данные: С=0.2 нФ, R=4кОм, L=6мГн, , .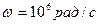

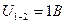Определить полную мощность, потребляемую цепью: S-?

Решение:

Определим величину индуктивного и емкостного сопротивлений на заданной частоте:

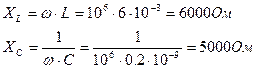
Ветви, содержащие катушку и конденсатор, соединены параллельно и их результирующее сопротивление равно:

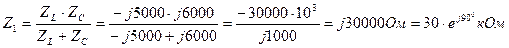
Результирующее сопротивление всей цепи равно:

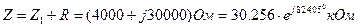
Величина тока данной цепи:

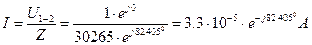
Определим полную мощность цепи:

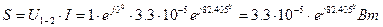
Полная мощность цепи равна: S=0.033мВт

Задача №2.

Исходные данные: J=0.1 A, E=125B,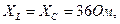

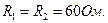
Методом наложения определить ток в :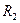

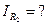
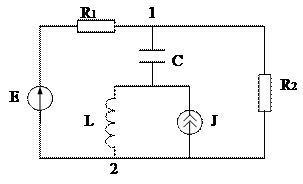Решение:

1. Отсоединим ветвь с источником тока, тогда схема примет вид:

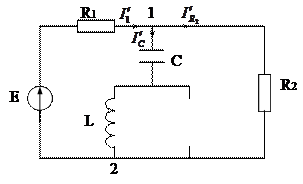По второму закону Киргофа для контуров 1- 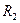- 2 и 1 - 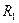- 2 запишем уравнения:

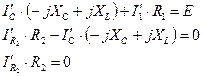(1)

По первому закону Киргофа для узла 1 запишем уравнение:

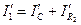(2)

Поскольку 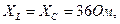то из второго уравнения (1) тогда имеем

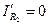
2. Закоротим ветвь с источником ЭДС Е, тогда схема принимает вид:

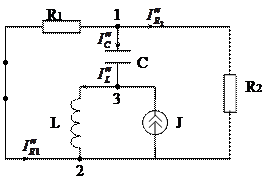По первому закону Кирхгофа для узлов 2 и 3 запишем уравнения:

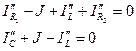
По второму закону Кирхгофа для контуров, не содержащих источника тока, запишем уравнение:

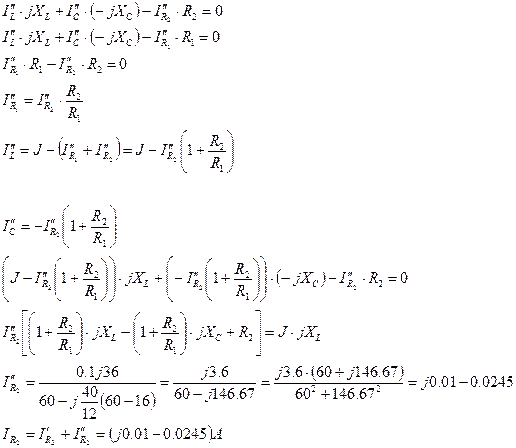
Задача №3.

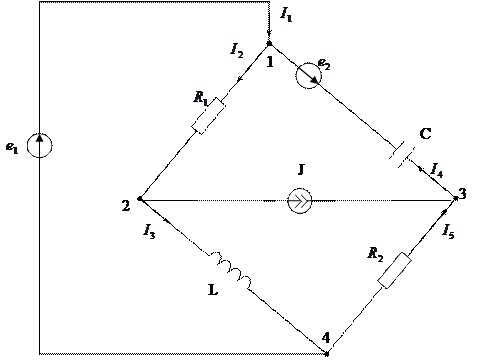
Составить уравнения Кирхгофа для мгновенных и комплексных значений электрических величин.

Решение:

1. Уравнения для комплексных значений.

Обозначим токи в отдельных ветвях цепи через 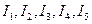и зададимся их направлением, а узлы пронумеруем цифрами 1, 2, 3 и 4.

По первому закону Кирхгофа запишем уравнения для трех узлов цепи:

Узел 1: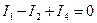

Узел 2: (1)

Узел 3: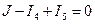

По второму закону Кирхгофа для двух контуров не содержащих источника тока, запишем уравнения:

Контур 1-3-4-1: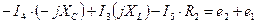

Контур 1-2-4-1: 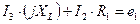(2)

Уравнения (1) и (2) в совокупности образуют систему пяти линейных алгебраических уравнений относительно пяти неизвестных токов 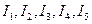. Решение приведенной системы уравнений позволяет эти токи определить.

2. Уравнения для мгновенных значений.

По первому закону Кирхгофа запишем уравнения для трех узлов цепи:

Узел 1: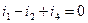

Узел 2: 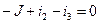(3)

Узел 3: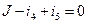

По второму закону Кирхгофа для двух контуров, не содержащих источника тока, запишем уравнения:

Контур 1-3-4-1: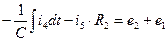

Контур 1-2-4-1: 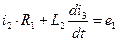(4)

Уравнения (3) и (4) в совокупности образуют систему пяти уравнений, позволяющих определить неизвестные токи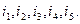

Задача №4.

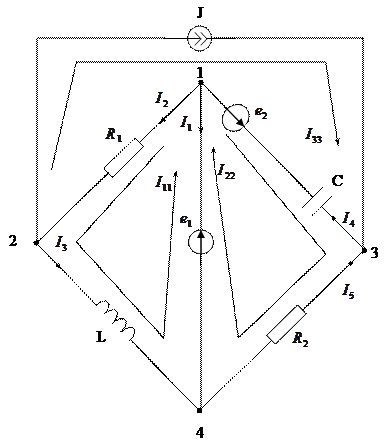Решение:

1. Метод контурных токов.

Рассмотрим три контура и обозначим токи в них через .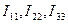

Очевидно, что 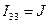, а для двух остальных контуров, не содержащих источника тока, запишем уравнения:

Контур 1-2-4-1: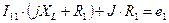

Контур 1-3-4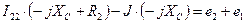-1: (1)

В результате имеем систему двух линейных алгебраических уравнений с двумя неизвестными токами 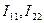. Решение этой системы уравнений позволяет определить отмеченные токи. Токи в отдельных ветвях определяются из соотношений:

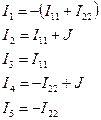(2)

2. Метод узловых напряжений.

Заземлим узел 1, тогда потенциал этого узла будет равен нулю 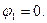Для определения потенциалов узлов 2, 3 и 4 составим систему уравнений:

(3)

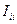- величина узлового тока в узле.

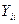- электропроводимость отдельного узла.

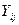- электропроводимость отдельной ветви между узлами I и j.

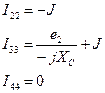
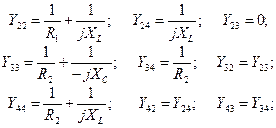
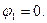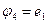Поскольку ветвь 4-1 содержит источник ЭДС и то и система уравнений (3) преобразуется к виду:

(4)

Решение системы (4) позволяет определить потенциалы узлов 2 и 3. Токи в ветвях определяются из соотношений:

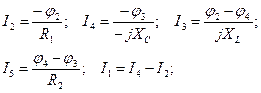
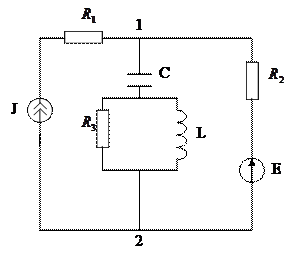
Задача №5.

Исходные данные: Е=100В,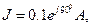

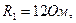
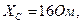
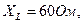
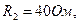
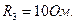
Методом эквивалентного генератора определить ток в -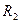

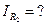
Решение:

Отсоединим ветвь с резистором 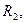а источник ЭДС перенесем в ветви 1-С- 2 и 1 – J – 2, тогда схема примет вид:

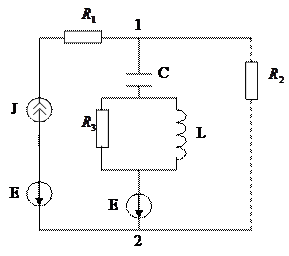Искомый ток в ветви с резистором 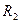определяется из соотношения:

где:

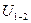- напряжение на резисторе,

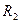- сопротивление резистора,

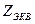- сопротивление цепи после отсоединения резистора.

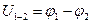
Для вычисления потенциалов узлов 1 и 2 воспользуемся методом узловых напряжений. Заземлим узел 2, тогда 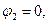а потенциал узла 1 определим из решения уравнения:

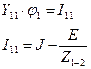
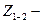сопротивление ветви 1-С-2,

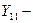электропроводимость узла 1.

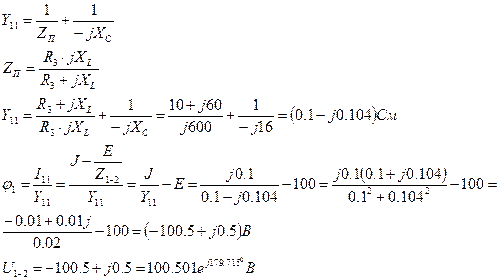
Закоротим зажимы источников ЭДС, зажимы источника тока разомкнем и определим эквивалентное сопротивление цепи:

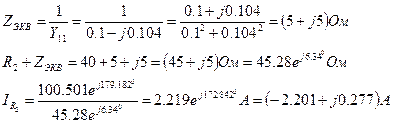
МинистерствоРоссийскойФедерации по связи и информатизации

Уральский технический институт связи и информатики (филиал)