
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сложение ускорений. Теорема Кориолиса
|
|
В дальнейшем без доказательства будем пользоваться соотношениями (доказано для вращательного движения):
1) 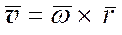 (1*), то есть вектор скорости любой точки тела равен векторному произведению угловой скорости на радиус вектор этой точки.
(1*), то есть вектор скорости любой точки тела равен векторному произведению угловой скорости на радиус вектор этой точки.
2) 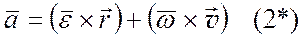 - векторное выражение ускорения точки при вращательном движении твердого тела.
- векторное выражение ускорения точки при вращательном движении твердого тела.
3) Так как 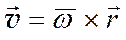 или
или 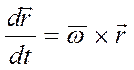 , по аналогии
, по аналогии 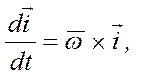 т.е.:
т.е.:
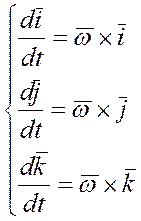 (3*)
(3*)
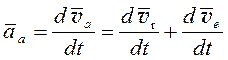 (3.3)
(3.3)
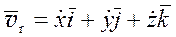 (3.4)
(3.4)
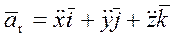 (3.5)
(3.5)
Дальнейший расчет зависит от характера переносного движения.
Сложение ускорений при непоступательном переносном движении. Теорема Кориолиса.
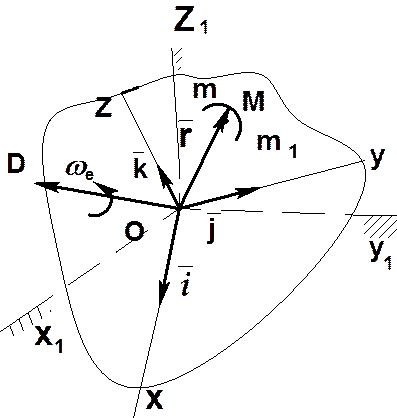
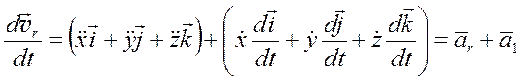 (3.6)
(3.6)
где 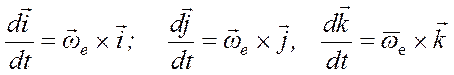 , (3.7)
, (3.7)
Тогда 
Окончательно:
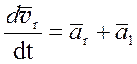 , где
, где  (3.8)
(3.8)
Скорость и ускорение в переносном движении точки M:
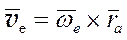 (3.9)
(3.9)
 (3.10)
(3.10)
 (3.11)
(3.11)
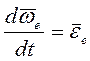 (3.12)
(3.12)
 (3.13)
(3.13)
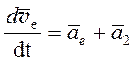 , где
, где  (3.14)
(3.14)

 (3.15)
(3.15)
-ускорение Кориолиса
Теорема Кориолиса
 (3.16)
(3.16)
Абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного, характеризующего изменение относительной скорости точки в относительном движении, переносного, характеризующего изменение переносной скорости в переносном движении, и кориолисова, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении.
Если переносное движение является поступательным,
то
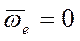 и
и 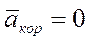
Абсолютное ускорение точки равно
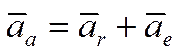 (3.17)
(3.17)
Вычисление относительного, переносного и кориолисова ускорений
При криволинейном относительном движении точки:
 (3.18)
(3.18)
Где 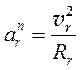 - относительное нормальное ускорение, направлено по радиусу кривизны к центру кривизны траектории относительного движения.
- относительное нормальное ускорение, направлено по радиусу кривизны к центру кривизны траектории относительного движения.
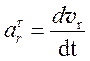 - относительное касательное ускорение, направлено по касательной к траектории относительного движения точки.
- относительное касательное ускорение, направлено по касательной к траектории относительного движения точки.
При вращательном переносном движении точки:
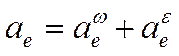 (3.19)
(3.19)
где  - переносное центростремительное ускорение точки, направлено по радиусу переносного вращения к оси переносного вращения;
- переносное центростремительное ускорение точки, направлено по радиусу переносного вращения к оси переносного вращения;
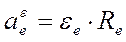 - переносное вращательное ускорение точки, направлено по касательной к траектории переносного вращения точки в данный момент времени. Здесь
- переносное вращательное ускорение точки, направлено по касательной к траектории переносного вращения точки в данный момент времени. Здесь  - радиус переносного вращения точки.
- радиус переносного вращения точки.
Кориолисово ускорение
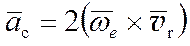
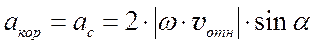 (3.20)
(3.20)
Направлен вектор  перпендикулярно плоскости, проходящей через вектора
перпендикулярно плоскости, проходящей через вектора  и
и 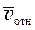 в ту сторону, откуда кратчайшее совмещение
в ту сторону, откуда кратчайшее совмещение  с
с 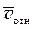 видно происходящим против хода часовой стрелки.
видно происходящим против хода часовой стрелки.
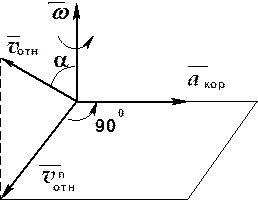
| 
|
Таким образом, окончательное выражение абсолютного ускорения точки при криволинейном относительном и вращательном переносном движении имеет вид:
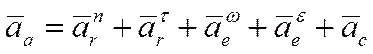 (3.21)
(3.21)
Примеры:
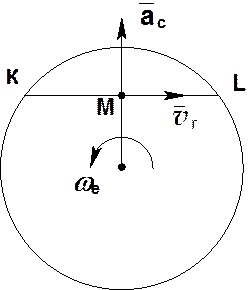
|
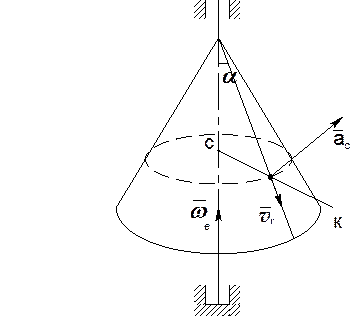
|