
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 2. Методами Эйлера и Рунге-Кутта 4-го порядка решить задачу Коши для систем дифференциальных уравнений
|
|
Задание 1.
Методами Эйлера и Рунге-Кутта 4-го порядка решить задачу Коши для систем дифференциальных уравнений, где xϵ [0, 1], y1(0) = y10, y2(0) = y20, шаг h = 0, 1. Построив графики, сравнить полученные численные решения с точным, приведенным в вариантах задания.
1. 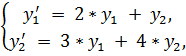
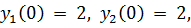
точное решение:
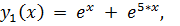

2. 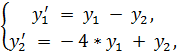
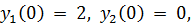
точное решение:
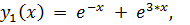
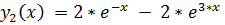
3. 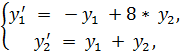
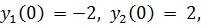
точное решение:
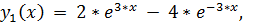
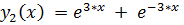
4. 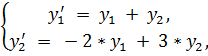
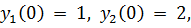
точное решение:
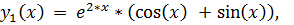
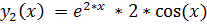
5. 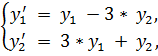
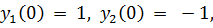
точное решение:
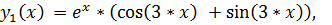
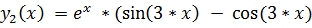 )
)
6. 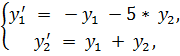
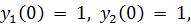
точное решение:
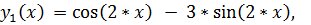
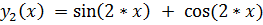
7. 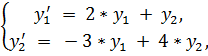
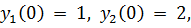
точное решение:
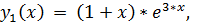
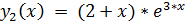
8. 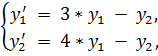
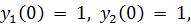
точное решение:
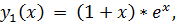
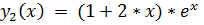
9. 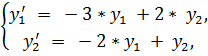
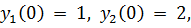
точное решение:
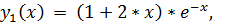
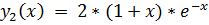
10. 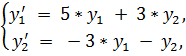
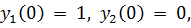
точное решение:

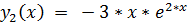
11. 

точное решение:
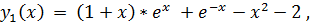
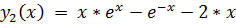
12. 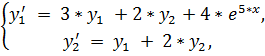
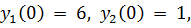
точное решение:
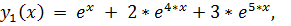
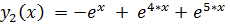
13. 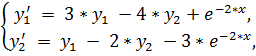
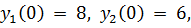
точное решение:
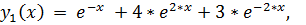
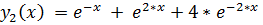
14. 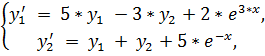
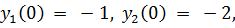
точное решение:
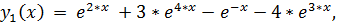
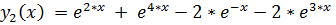
15. 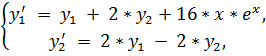
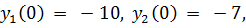
точное решение:
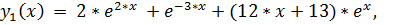
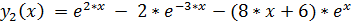
16. 
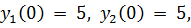
точное решение:
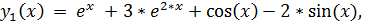
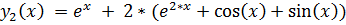
17. 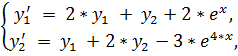
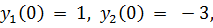
точное решение:
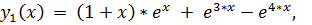
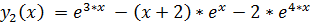
18. 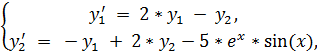
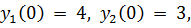
точное решение:
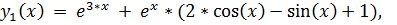
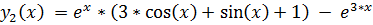
19. 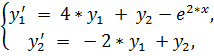
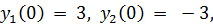
точное решение:
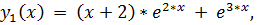
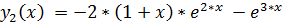
20. 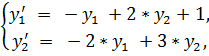
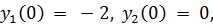
точное решение:
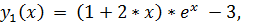
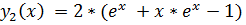
21. 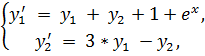
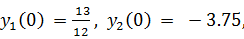
точное решение:
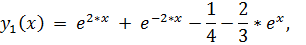

22. 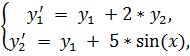
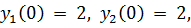
точное решение:
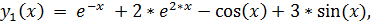
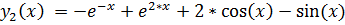
23. 
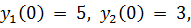
точное решение:
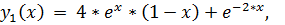
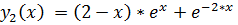
24. 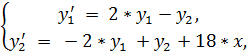
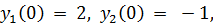
точное решение:
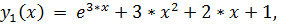
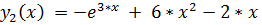
25. 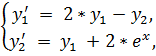
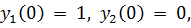
точное решение:
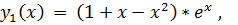
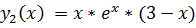 .
.
Задание 2.
Методами Эйлера и Рунге-Кутта 4-го порядка решить задачу Коши для дифференциального уравнения второго порядка, где xϵ [0, 1], y(0) = y10, y’(0) = y20, шаг h = 0, 1. Построив графики, сравнить полученные численные решения с точным, приведенным в вариантах задания.
1. 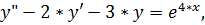

точное решение: 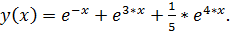
2. 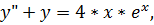
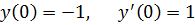
точное решение: 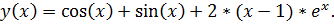
3. 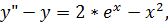

точное решение: 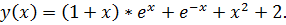
4. 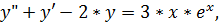
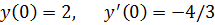
точное решение: 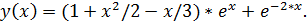
5. 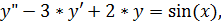

точное решение: 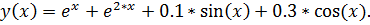
6. 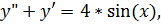
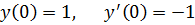
точное решение: 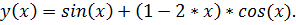
7. 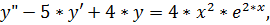
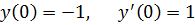
точное решение: 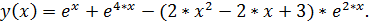
8. 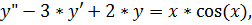

точное решение:
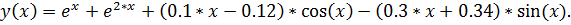
9. 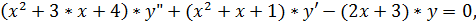

точное решение: 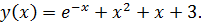
10. 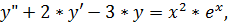
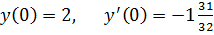
точное решение: 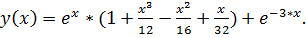
11. 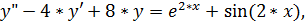

точное решение:
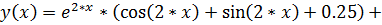
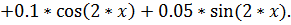
12. 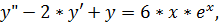

точное решение: 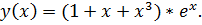
13. 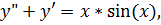

точное решение: 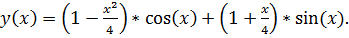
14. 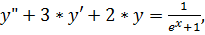

точное решение: 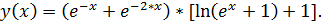
15. 

точное решение: 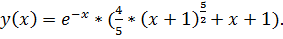
16. 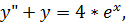
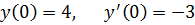
точное решение: 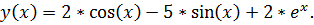
17. 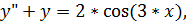
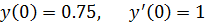
точное решение: 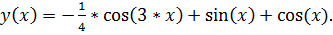
18. 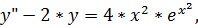

точное решение: 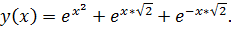
19. 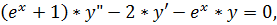
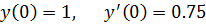
точное решение: 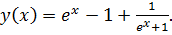
20. 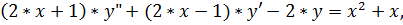
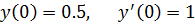
точное решение: 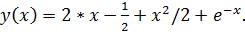
21. 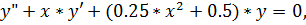

точное решение: 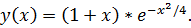
22. 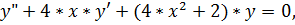

точное решение: 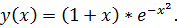
23. 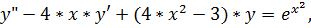

точное решение: 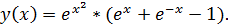
24. 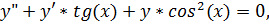

точное решение: 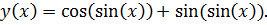
25. 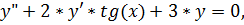

точное решение: 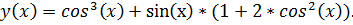
|