
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теория метода. Цель работы: получение стоячих волн в воздухе и применение их для определения длины, частоты и скорости звуковых волн.
|
|
Лабораторная работа №48
ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА И ЧАСТОТЫ КОЛЕБАНИЙ КАМЕРТОНА МЕТОДОМ СТОЯЧЕЙ ВОДЫ
Цель работы: получение стоячих волн в воздухе и применение их для определения длины, частоты и скорости звуковых волн.
Приборы и принадлежности: металлическая труба-резонатор; прозрачная водомерная трубка со шкалой; сосуд с водой, соединённый шлангом с обеими трубами; два различных камертона; резиновый молоточек.
ТЕОРИЯ МЕТОДА
Если в упругой (твердой, жидкой или газообразной) среде возбудить колебания её частиц, то вследствие взаимодействия между частицами эти колебания будут распространяться с определенной скоростью в среде. Процесс распространения колебаний в пространстве называется волновым процессом или бегущей волной.
В зависимости от направления колебаний частиц среды по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникать лишь в таких средах, которые обладают сопротивлением сдвигу. Возникновение продольных упругих волн возможно в том случае, когда среда оказывает сопротивление деформации сжатия или растяжения. Поэтому в жидкостях и газах могут возникать только продольные волны. В твердых телах возможно возникновение как продольных, так и поперечных волн.
Распространяющиеся в воздухе упругие волны, в которых частота ν колебаний частиц воздуха находиться в пределах от 16 Гц до 20 кГц, достигнув человеческого уха, вызывает ощущение звука. В соответствии с этим упругие волны в любой среде, имеющие частоту, которая заключена в указанных пределах, тоже называют звуковыми волнами или просто звуком. Упругие волны с частотами меньше 16 Гц называется инфразвуком; волны с частотами, превышающими 20 кГц, называются ультразвуком. Инфра- и ультразвуки человеческое ухо не слышит, но они могут улавливаться некоторыми живыми существами и регистрироваться специальными приборами.
При одновременном распространении в пространстве нескольких волн, в том числе звуковых, от различных источников происходит их наложение (суперпозиция) без взаимного возмущения. При наложении волн, дающих одинаковой частотой и постоянной разностью начальных фаз, наблюдается явление интерференции. Оно заключается в усилении колебаний в одних точках пространства и в ослаблении их в других точках. При интерференции двух плоских волн с одинаковой частотой и амплитудой, которые распространяются в противоположных направлениях, возникает колебательный процесс, называемый стоячей волной. Практически стоячие волны можно получить при отражении бегущей волны от преграды. Падающая на преграду волна и бегущая ей навстречу отраженная волна интерферируют друг с другом и образуют стоячую волну.
Пусть звуковая волна, возбуждаемая в воздухе в точке 0, распространяется по направлению оси x. Уравнение этой волны в произвольной точке B запишем в виде
(1)
где - смещение частиц среды от положения равновесия, a – амплитуда волны,
, ω – круговая частота (ω = 2π ν), ν – частота, t – время, x – расстояние от начала координат (0) до точки В, u – фазовая скорость волны.
После прохождения расстояния l до преграды эта звуковая волна отражается от неё. В результате отражения от более плотной среды, чем воздух, фаза волны изменяется на π. Уравнение отраженной волны запишем в виде
(2)
где - смещение частиц среды в отраженной волне, (2l – x) – расстояние, пройденное волной от начала координат (точка 0) до преграды и обратно от этой преграды до точки В. Знак минус в последней формуле (2) учитывает сдвиг фазы колебаний на π в точке отражения.
Смещение частиц среды в результате наложения падающей и отраженной волн получим, складывая выражения (1) и (2):
(3)
Используя тригонометрическое соотношение
формулу (3) можно привести к виду
(4)
Выражение (4) называется уравнением стоячей волны. Проведем его анализ.
Аргумент синуса зависит от координаты точки x, но не зависит от времени t. На основании модуль выражения можно рассматривать в качестве амплитуды стоячей волны (берется модуль, так как амплитуда всегда считается положительной величиной).
В соответствии со сказанным выше амплитуда стоячей волны
(5)
зависит от координаты x. В точках, в которых для аргумента синуса выполняется условие
(6)
где n = 0, 1, 2…, модуль синуса равен единице; в этих точках амплитуда колебаний А достигает максимального значения, равного 2a. Эти точки называются пучностями стоячей волны.
В точках, в которых выполняется условие
(7)
где также n = 0, 1, 2…, синус равен нулю и амплитуда колебаний обращается в ноль. Эти точки называются узлами стоячей волны.
Определим расстояние между двумя соседними узлами. С этой целью преобразуем левую часть уравнения (7):
(8)
Здесь учтено, что ω = 2π /Т и Т u = λ, причем Т = 1/v – период колебаний и λ – длина волны. Заменив теперь левую часть выражения (7) на выражение (8), получим
откуда следует, что
(9)
Это уравнение определяет координату n –го узла. При постоянных λ и l величина xn зависит только от n. Поскольку дискретная величина n изменяется на, то расстояние между двумя соседними узлами можно найти, положив, например, n1 = 1 и n2 = 2, тогда
(10)
Выражение типа (10) справедливо не только для двух любых соседних узлов, но и для двух соседних пучностей стоячей волны:
(11)
Отсюда следует, что расстояние между соседним узлом и пучностью стоячей волны составит λ /4.
Множитель в уравнении (4) при переходе через нулевое значение меняет знак. Это означает, что фазы колебаний по обе стороны от узла отличается на π. Следовательно, точки, лежащие по разные стороны от любого узла, совершают колебания в противофазе. Напротив, все точки, заключенные между двумя соседними узлами, колеблются в одинаковой фазе, т.е. синфазно. На рис. 1 схематически приведено положение колеблющихся точек среды в поперечной стоячей волне для двух разных моментов времени t1 и t2 > t1 при движении точек к положению равновесия. Стрелки показывают направление движения частиц среды. Из рисунка видно, что волна как бы стоит на месте, так как положения узлов и пучностей не меняются с течением времени; отсюда и происходит название волны – стоячая волна.
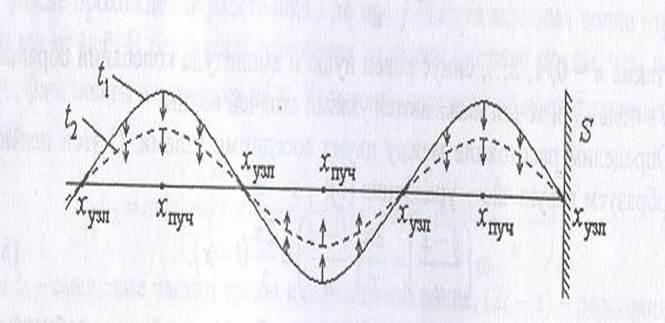
Рис. 1. Смещение частиц среды в фиксированные моменты времени t1 и t2
в стоячей волне: xпуч – положения пучностей, xузл – положения узлов,