
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розрахунковий опір ґрунту основи, його визначення та використання на практиці.
|
|
Розрахунковий опір грунту. Тиск 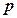 , при якому крива залежності
, при якому крива залежності 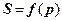 (рис. 7.2) умовно переходить від прямолінійної ділянки до криволінійної (кінець ІІ- ї, початок ІІІ- ї фази) називається розрахунковим опором грунту
(рис. 7.2) умовно переходить від прямолінійної ділянки до криволінійної (кінець ІІ- ї, початок ІІІ- ї фази) називається розрахунковим опором грунту 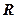 або першим критичним тиском
або першим критичним тиском 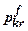 . Це навантаження є цілком безпечним, тому що зони граничного стану будуть займати незначні області під сторонами фундаменту і грунт практично знаходиться в фазі ущільнення.
. Це навантаження є цілком безпечним, тому що зони граничного стану будуть займати незначні області під сторонами фундаменту і грунт практично знаходиться в фазі ущільнення. 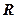 є максимальним тиском (навантаженням), при якому можна використовувати для розрахунків осідань фундаментів лінійні залежності між деформаціями і напруженнями. Якщо
є максимальним тиском (навантаженням), при якому можна використовувати для розрахунків осідань фундаментів лінійні залежності між деформаціями і напруженнями. Якщо 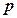 перевищує
перевищує 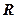 , то для визначення осідань фундаментів необхідно використовувати залежності, що враховують криволінійність функції
, то для визначення осідань фундаментів необхідно використовувати залежності, що враховують криволінійність функції 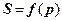 .
.
 Задача з визначення першого критичного тиску розв’язана М.П. Пузиревським у 1929р. Розглянемо дію рівномірно розподіленого навантаження
Задача з визначення першого критичного тиску розв’язана М.П. Пузиревським у 1929р. Розглянемо дію рівномірно розподіленого навантаження 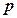 на смузі шириною
на смузі шириною 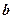 при наявності бічного завантаження
при наявності бічного завантаження 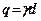 , викликаного заглибленням фундаменту на величину
, викликаного заглибленням фундаменту на величину 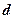 (рис. 8.5). Вертикальні стискуючі напруження від власної ваги грунту
(рис. 8.5). Вертикальні стискуючі напруження від власної ваги грунту 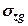 у точці
у точці 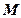 на глибині
на глибині 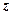 нижче підошви фундамету становлять
нижче підошви фундамету становлять
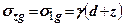 , де (8.3)
, де (8.3)
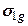 - головні напруження, викликані власною вагою грунту.
- головні напруження, викликані власною вагою грунту.
Приймемо припущення про гідростатичний розподіл напружень від власної ваги грунту, тобто 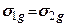 (в певній мірі це неправильно -
(в певній мірі це неправильно - 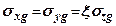 (7.24)).
(7.24)).
Вище було показано, що в умовах плоскої задачі величини головних напружень від дії навантаження 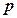 визначаються за формулами (7.21), (7.22)---(
визначаються за формулами (7.21), (7.22)---(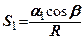 і
і 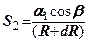 )
)
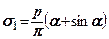 ;
; 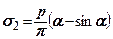
Для будь-якої точки 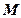 запишемо величини головних напружень, викликаних дією тиску
запишемо величини головних напружень, викликаних дією тиску 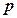 з урахуванням власної ваги грунту, використовуючи (7.21), (7.22)
з урахуванням власної ваги грунту, використовуючи (7.21), (7.22)
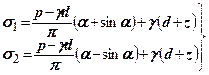 (8.4)
(8.4)
Зменшення 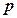 на величину
на величину 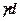 в (8.4) викликане заглибленням фундаменту.
в (8.4) викликане заглибленням фундаменту.
Підставимо (8.4) в умову граничної рівноваги зв’язного грунту (8.2) 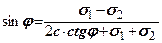 і розв’яжемо це рівняння відносно
і розв’яжемо це рівняння відносно 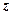
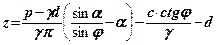 (8.5)
(8.5)
Знайдемо максимальну глибину розподілу зон граничної рівноваги 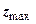 при навантаженні
при навантаженні 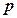 . Для цього похідну
. Для цього похідну 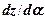 прирівняємо до
прирівняємо до 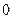
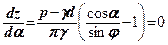 (8.6)
(8.6)
Умова (8.6) буде виконуватись коли 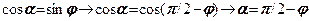 , або
, або 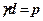 . Підставимо
. Підставимо 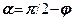 в (8.5)
в (8.5)
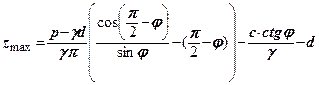 (8.7)
(8.7)
Розв’яжемо (8.7) відносно 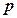
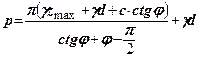 (8.8)
(8.8)
Як видно, рівняння (8.8) має два невідомих 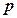 і
і 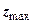 . Якщо прийняти
. Якщо прийняти 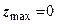 , тобто зовсім не допускати розповсюдження зон граничної рівноваги під підошвою фундаменту, тоді (8.8) прийме вигляд
, тобто зовсім не допускати розповсюдження зон граничної рівноваги під підошвою фундаменту, тоді (8.8) прийме вигляд
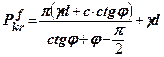 (8.9)
(8.9)
Діючі норми допускають розповсюдження зон зсувів на глибину 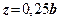 . При цьому вважається, що при такій умові залежність
. При цьому вважається, що при такій умові залежність 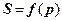 ще залишається близькою до лінійної. З урахуванням останнього можна записати
ще залишається близькою до лінійної. З урахуванням останнього можна записати
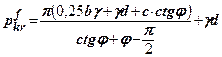 (8.10)
(8.10)
Позначимо: 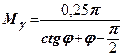 ;
; 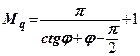 ;
; 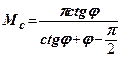
Тоді
 (8.11)
(8.11)
 Коефіцієнти
Коефіцієнти 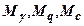 залежать тільки від кута внутрішнього тертя грунту і визначаються за допомогою спеціальних таблиць, вміщених в будівельних нормах. Крім того, формула (7) СНиП 2.02.01-83 [24] враховує додатково вид грунту, особливості будівлі, метод визначення характеристик міцності, ширину фундаменту, наявність підвалу і різницю в питомій вазі грунту. Ця формула має вигляд
залежать тільки від кута внутрішнього тертя грунту і визначаються за допомогою спеціальних таблиць, вміщених в будівельних нормах. Крім того, формула (7) СНиП 2.02.01-83 [24] враховує додатково вид грунту, особливості будівлі, метод визначення характеристик міцності, ширину фундаменту, наявність підвалу і різницю в питомій вазі грунту. Ця формула має вигляд
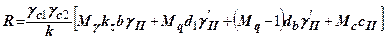 , (8.12)
, (8.12)
 де
де 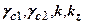 - коефіцієнти, які відповідно враховують вид грунту, споруди, метод визначення
- коефіцієнти, які відповідно враховують вид грунту, споруди, метод визначення 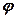 і
і 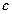 , ширину фундаменту;
, ширину фундаменту; 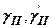 -питома вага грунту відповідно нижче і вище підошви фундаменту;
-питома вага грунту відповідно нижче і вище підошви фундаменту; 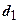 - глибина закладення фундаменту від підлоги підвалу;
- глибина закладення фундаменту від підлоги підвалу; 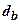 - глибина підвалу від рівня планувальної відмітки. Член
- глибина підвалу від рівня планувальної відмітки. Член 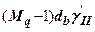 враховує наявність підвалу. При його відсутності
враховує наявність підвалу. При його відсутності 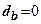 .
.