
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сколько сторон имеет правильный n-угольник, если его каждый угол равен 135°?
|
|
Сумма всех внутренних углов выпуклого n-угольника определяется из формулы: S=180°·(n-2), где n - количество углов (сторон) выпуклого n-угольника.
Зная, что каждый угол данного n-угольника равен 135°, составим уравнение:
180°·(n-2)=135°·n. Раскроем скобки. 180n-360=135n ⇒ 180n-135n=360 ⇒ 45n=360, разделим обе части равенства на 45 и получаем число углов (сторон) n=8.
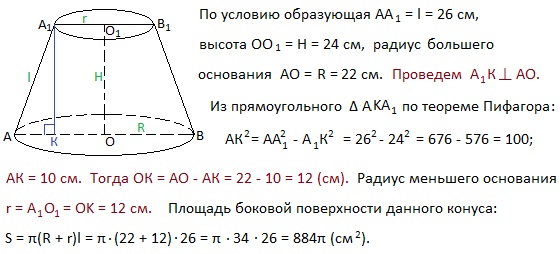
19. Образующая, высота и радиус большего основания усеченного конуса соответственно равны 26 см, 24 см, 22 см. Вычислите боковую поверхность этого конуса. Решаем. Боковую поверхность усеченного конуса вычисляют по формуле: S=π (R+r)l, где R — радиус большего основания конуса (по условию R=22 см), r — радиус меньшего основания конуса (неизвестен), l — образующая конуса (по условию l=26 см). Потребуется найти радиус меньшего основания конуса. Рассмотрим усеченный конус с осевым сечением AA1B1B, образующей AA1 и высотой OO1 (по условию OO1=24 см).
20. Решите уравнение:

21. Найдите значение выражения.

22. Решить неравенство: 2sin2x-4sinxcosx+9cos2x> 0. Решаем. Разделим обе части неравенства на cos2x. Так как cos2x> 0, то знак неравенства не изменится. Получаем:
2tg2x-4tgx+9> 0; делаем замену: пусть tgx=y. Получаем неравенство: 2y2-4y+9> 0. Это неравенство будет верным при любом значении у. Убедимся — найдем дискриминант квадратного уравнения 2y2-4y+9=0.
D=b2-4ac=16-4∙ 2∙ 9=16-72=-56< 0, что означает- корней нет, т. е. график уравнения (парабола) не пересечет ось Ох. Ветви параболы направлены вверх, следовательно, при любом значении у мы будем получать только положительные значения f(y). Все еще сомневаетесь? Тогда найдите координаты вершины параболы O’(m; n), где m= -b/(2a)=4: 4=1; n=f(m) =f(1)=2-4+9=7. O’(1; 7) — это самая нижняя точка графика. Все остальные точки лежат выше. Итак, у -любое число. Мы делали замену tgx=y. Значит, и х может быть любым числом. Ответ: (-∞; +∞).
23. В геометрической прогрессии разность между шестым и четвертым членами равна 192, а разность между третьим и первым членами равна 24. Найдите сумму первых восьми членов этой прогрессии.

24. Найти длину меньшей диагонали параллелограмма, построенного на векторах

25. У деда 9 сыновей, у каждого его сына по 4 сына, а у каждого внука деда по 3 дочери. Сколько правнучек у деда? Рассуждаем. Если у каждого сына по 4 своих сына, то у деда 9·4=36 внуков. Так как у каждого внука по 3 дочери, то правнучек у деда 36·3= 108.
вариант 0021
5. Решите неравенство:
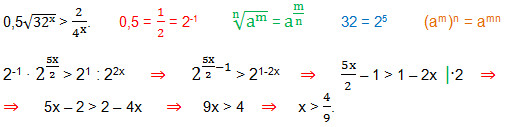
6. Упростите выражение:
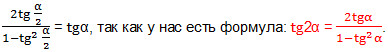
17. f(x)=6x2+8x+5, F(-1)=3. Найдите F(-2).
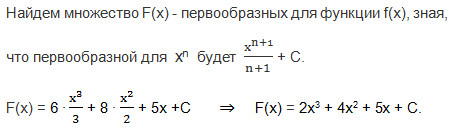
Найдем С, зная, что F(-1) = 3.
3 = 2 ∙ (-1)3 + 4 ∙ (-1)2 + 5 ∙ (-1) + C;
3 = -2 + 4 – 5 + C;
C = 6.
Таким образом первообразная F(x) = 2x3 + 4x2 + 5x + 6. Найдем F(-2).
F(-2) = 2∙ (-2)3+4∙ (-2)2+5∙ (-2)+6 = -16+16-10+6=-4.
20. Избавьтесь от иррациональности в знаменателе
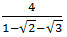
Решение основано на основном свойстве дроби, позволяющим умножать числитель и знаменатель дроби на одно и то же, не равное нулю число. Чтобы избавиться от знаков радикала в знаменателе дроби, обычно используют ФСУ (формулы сокращенного умножения). Ведь если разность двух радикалов умножить на их сумму, то получится разность квадратов корней, т.е. получится выражение без знаков радикалов.
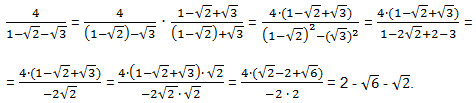
21. Упростить выражение:
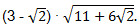
Решим этот пример двумя способами. 1) Представим подкоренное выражение второго множителя в виде квадрата суммы двух выражений, т.е. в виде(a + b)2. Это позволит нам извлечь арифметический квадратный корень.
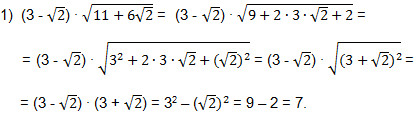
2) Возведем первый множитель в квадрат и внесем его под знак арифметического квадратного корня второго множителя.
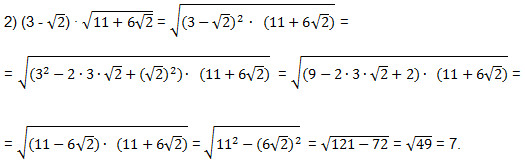
Решайте удобным для себя способом!
22. Найдите (х1∙ у1+х2∙ у2), где (хn; yn) – решения системы уравнений:
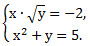
Так как арифметический квадратный корень можно извлечь только из неотрицательного числа, то допустимыми значениями переменной у служат все числа, удовлетворяющие неравенству y≥ 0. Так как произведение в первом уравнении системы равно отрицательному числу, то должно выполняться условие: x< 0. Выразим х из первого уравнения и подставим его значение во второе уравнение. Решим получившееся уравнение относительно у, а затем найдем значения х, соответствующие полученным ранее значениям у.

23. Решить неравенство: 7sin2x+cos2x> 5sinx.
Так как по основному тригонометрическому тождеству: sin2x+cos2x=1, то представив данное неравенство в виде 6sin2x+ sin2x +cos2x> 5sinx и применив основное тригонометрическое тождество, получаем: 6sin2x+ 1> 5sinx. Решаем неравенство:
6sin2x-5sinx+1 > 0. Сделаем замену: sinx=y и получим квадратичное неравенство:
6y2-5y+1> 0. Решим это неравенство методом интервалов, разложив левую часть на множители. Для этого найдем корни полного квадратного уравнения:
6y2-5y+1=0. Дискриминант D=b2-4ac=52-4∙ 6∙ 1=25-24=1. Тогда получаем у1 и у2:
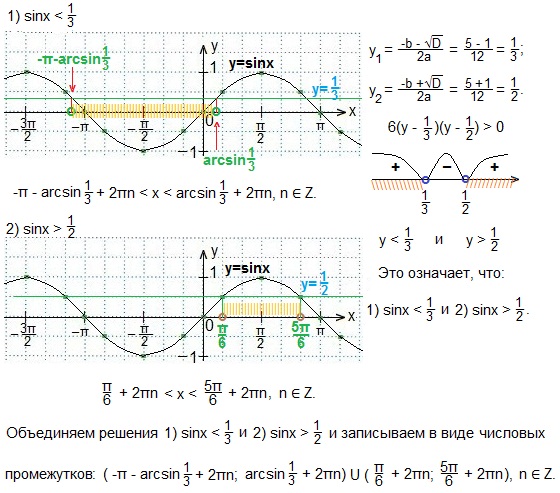
24. В основании прямой призмы лежит правильный треугольник, площадь которого равна 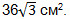 Вычислите площадь боковой поверхности призмы, если ее объем равен 300 см3.
Вычислите площадь боковой поверхности призмы, если ее объем равен 300 см3.
Пусть нам дана правильная треугольная призма АВСА1В1С1, в основании которой лежит правильный Δ АВС, его площадь нам известна. Применив формулу площади равностороннего треугольника, мы найдем сторону нашего треугольника АВС. Так как объем прямой призмы, вычисляется по формуле V=Sосн.∙ H, и нам также известен, то можно найти Н — высоту призмы. Боковое ребро призмы будет равно высоте призмы: AA1=H. Зная сторону основания и длину бокового ребра призмы можно найти площадь ее боковой поверхности по формуле: Sбок.=Pосн.∙ H.

25. На школьной викторине было предложено 20 вопросов. За каждый правильный ответ участнику начисляли 12 очков, а за каждый неправильный списывали 10 очков. Сколько правильных ответов дал один из участников, если он отвечал на все вопросы и набрал 86 очков?
Пусть участник дал х правильных ответов. Тогда неправильных у него (20-х) ответов. Зная, что за каждый правильный ответ ему начисляли 12 очков, а за каждый неправильный списывали 10 очков и при этом он набрал 86 очков, составим уравнение:
12х-10·(20-х)=86;
12х-200+10х=86;
22х=286 ⇒ х=286: 22 ⇒ х=13. Участник дал 13 правильных ответов.