
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Идея метода зеркальных изображений
|
|
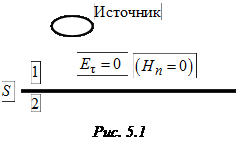 Рассмотрим следующую ситуацию. Имеется источник поля, расположенный над бесконечной идеально проводящей поверхностью S (рис. 5.1), которая делит пространство на два полупространства – 1 и 2. В полупространстве 2 поле отсутствует, так как оно экранировано от источника. Требуется найти поле в полупространстве 1, которое, очевидно, не совпадает с полем источника в отсутствие экрана. С формально-математической точки зрения влияние экрана сказывается в том, что на его поверхности должно выполняться граничное условие
Рассмотрим следующую ситуацию. Имеется источник поля, расположенный над бесконечной идеально проводящей поверхностью S (рис. 5.1), которая делит пространство на два полупространства – 1 и 2. В полупространстве 2 поле отсутствует, так как оно экранировано от источника. Требуется найти поле в полупространстве 1, которое, очевидно, не совпадает с полем источника в отсутствие экрана. С формально-математической точки зрения влияние экрана сказывается в том, что на его поверхности должно выполняться граничное условие
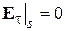 ,
, 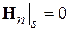 . (5.1)
. (5.1)
Метод зеркальных изображений позволяет рассчитать поле в полупространстве 1 путем замены экрана зеркальным изображением источника в нем. Искомое поле представляется тогда суммой полей истинного источника и его зеркального изображения. На месте удаленного экрана должно при этом обеспечиваться выполнение условия (5.1). Рассмотрим применение метода на примере вертикального и горизонтального диполя Герца с моментом 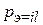 (
(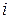 -ток, l- длина диполя) (рис. 5.2). На основе метода зеркальных изображений откажемся от проводящей границы раздела и запишем выражение для напряженности электрического поля, создаваемого в дальней зоне диполя Герца с моментом pэв следующем виде:
-ток, l- длина диполя) (рис. 5.2). На основе метода зеркальных изображений откажемся от проводящей границы раздела и запишем выражение для напряженности электрического поля, создаваемого в дальней зоне диполя Герца с моментом pэв следующем виде: 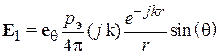 . На фиктивной границе двух сред орт
. На фиктивной границе двух сред орт 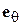 можно представить как сумму нормальной и касательной к поверхности, составляющей со своими амплитудными коэффициентами
можно представить как сумму нормальной и касательной к поверхности, составляющей со своими амплитудными коэффициентами 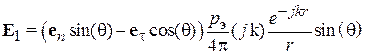 . Из приведенного выражения видно, что одиночной диполь имеет отличную от нуля касательную к поверхности составляющую электрического поля, что не удовлетворяет ГУ (5.1). В связи с этим необходимо осуществить выбор расположения и фазы дипольного момента изображения, при которых обеспечивается выполнение ГУ. Поле мнимого изображения должно скомпенсировать касательную составляющую электрического поля оригинала, следовательно, моменты оригинала и изображения должны быть синфазными. В этом случае поле, создаваемое изображением, запишется как
. Из приведенного выражения видно, что одиночной диполь имеет отличную от нуля касательную к поверхности составляющую электрического поля, что не удовлетворяет ГУ (5.1). В связи с этим необходимо осуществить выбор расположения и фазы дипольного момента изображения, при которых обеспечивается выполнение ГУ. Поле мнимого изображения должно скомпенсировать касательную составляющую электрического поля оригинала, следовательно, моменты оригинала и изображения должны быть синфазными. В этом случае поле, создаваемое изображением, запишется как 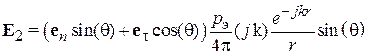 . В результате суммарное поле будет удовлетворять ГУ (5.1) и таким образом, поле в дальней зоне системы из двух источников окажется эквивалентным полю диполя над проводящей поверхностью.
. В результате суммарное поле будет удовлетворять ГУ (5.1) и таким образом, поле в дальней зоне системы из двух источников окажется эквивалентным полю диполя над проводящей поверхностью.
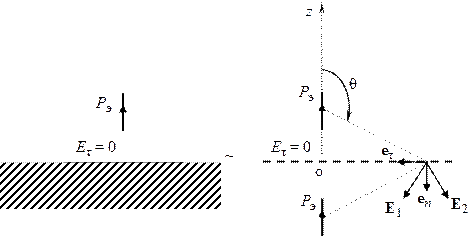
Рис. 5.2
Повторяя изложенные рассуждения для горизонтально расположенного диполя можно сделать вывод, что в этом случае моменты должны быть противофазными.
5.2. Применение метода зеркальных изображений к антеннам,
размещенным над проводящей плоскостью
Как известно, любую антенну можно представить совокупностью элементарных электрических и магнитных диполей Герца. Поэтому очевидна законность переноса метода зеркальных изображений и на этот случай. Суть метода полностью сохраняется: чтобы найти поле антенны в полупространстве 1, нужно отбросить экран, а его действие заменить действием зеркального изображения антенны. Необходимо лишь выяснить связь между характеристиками направленности реальной антенны и ее зеркального отображения. Для удобства анализа рассмотрим отдельно случай антенны с вертикально- и горизонтально-поляризованным полями излучения.
|
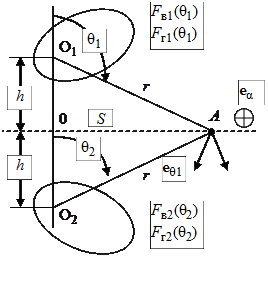 чала в этой точке поле антенны 1. Как известно, в поле излучения вектор электрического поля
чала в этой точке поле антенны 1. Как известно, в поле излучения вектор электрического поля 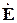 перпендикулярен направлению распространения, т. е. в данном случае - лучу О1 А; в то же время этот вектор, по нашему предположению, поляризован в вертикальной плоскости. Следовательно, он должен быть ориентирован по орту
перпендикулярен направлению распространения, т. е. в данном случае - лучу О1 А; в то же время этот вектор, по нашему предположению, поляризован в вертикальной плоскости. Следовательно, он должен быть ориентирован по орту 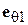 . Поле излучения пропорционально характеристике направленности по направлению луча О1 А. Характеристика направленности антенны 1 записывается как функция угла
. Поле излучения пропорционально характеристике направленности по направлению луча О1 А. Характеристика направленности антенны 1 записывается как функция угла 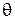 , отсчитываемого от вертикали. Следовательно, ее значение по направлению луча О1 А есть
, отсчитываемого от вертикали. Следовательно, ее значение по направлению луча О1 А есть 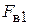 (
(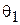 ). Наконец, выражение для поля
). Наконец, выражение для поля 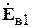 [В/м] должно содержать множитель, учитывающий запаздывание волны по фазе и убывание ее по амплитуде обратно пропорционально расстоянию от антенны. Этот множитель - функция Грина
[В/м] должно содержать множитель, учитывающий запаздывание волны по фазе и убывание ее по амплитуде обратно пропорционально расстоянию от антенны. Этот множитель - функция Грина 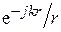 . Учитывая изложенное, получим
. Учитывая изложенное, получим
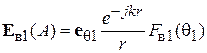 . (5.2)
. (5.2)
Аналогичным образом записывается поле зеркального изображения в точке А:
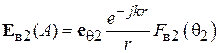 , (5.3)
, (5.3)
где 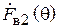 – характеристика направленности антенны 2. Угол
– характеристика направленности антенны 2. Угол 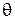 по-прежнему отсчитывается от вертикали, так что в данном случае он равен
по-прежнему отсчитывается от вертикали, так что в данном случае он равен 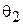 (см. рис. 5.3).
(см. рис. 5.3).
Чтобы поле 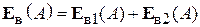 , полученное суммированием (5.2) и (5.3), имело нулевую касательную составляющую относительно S, значения
, полученное суммированием (5.2) и (5.3), имело нулевую касательную составляющую относительно S, значения 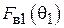 и
и 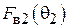 должны совпадать. Только в этом случае касательные составляющие обоих полей взаимно компенсируются. Заметим, что углы
должны совпадать. Только в этом случае касательные составляющие обоих полей взаимно компенсируются. Заметим, что углы 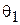 и
и 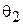 в данном рассмотрении жестко связаны:
в данном рассмотрении жестко связаны: 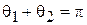 . Поэтому
. Поэтому 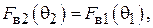
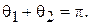 Это равенство означает, что характеристика направленности антенны 2 должна быть зеркальным отражением характеристики направленности антенны 1 (см. рис. 5.3), а антенны должны быть возбуждены синфазно.
Это равенство означает, что характеристика направленности антенны 2 должна быть зеркальным отражением характеристики направленности антенны 1 (см. рис. 5.3), а антенны должны быть возбуждены синфазно.
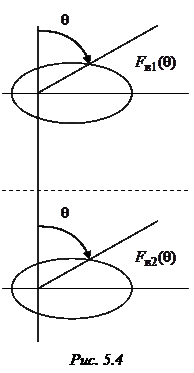 Особо выделим случай, когда ДН антенны 1 симметрична относительно направления
Особо выделим случай, когда ДН антенны 1 симметрична относительно направления 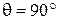 (рис. 5.4). В таком случае ее зеркальное изображение будет совпадать с оригиналом. Следовательно,
(рис. 5.4). В таком случае ее зеркальное изображение будет совпадать с оригиналом. Следовательно,
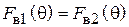 . (5.4)
. (5.4)
Горизонтальная поляризация. В данном случае выражение для поля антенны 1 в точке А 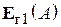 будет отличаться от выражения (5.3). Во-первых, вектор
будет отличаться от выражения (5.3). Во-первых, вектор 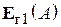 , который должен быть перпендикулярен О1 А (см. рис. 5.3) и одновременно горизонтально поляризован, будет направлен по орту
, который должен быть перпендикулярен О1 А (см. рис. 5.3) и одновременно горизонтально поляризован, будет направлен по орту 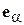 , перпендикулярному плоскости рисунка. Во-вторых, характеристика направленности имеет индекс «г», а не «в». Таким образом,
, перпендикулярному плоскости рисунка. Во-вторых, характеристика направленности имеет индекс «г», а не «в». Таким образом,
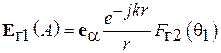 . (5.5)
. (5.5)
Поле антенны 2 также поляризовано по орту 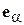 :
:
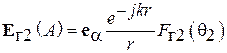 . (5.6)
. (5.6)
Сумма векторов (5.5) и (5.6) должна обратиться в нуль, поскольку орт 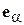 касателен к S. Следовательно, значения
касателен к S. Следовательно, значения 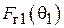 и
и 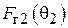 должны быть равны и противоположны по знаку:
должны быть равны и противоположны по знаку:
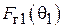 = -
= - 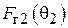 ,
, 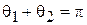 . (5.7)
. (5.7)
Таким образом, характеристики направленности антенн являются зеркальными изображениями друг друга, но, согласно (5.7) в отличие от вертикальной поляризации (см. (5.4)), антенны должны быть возбуждены в противофазе.
В особом случае, когда характеристики направленности симметричны относительно 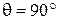 , получим следующее соотношение между ними:
, получим следующее соотношение между ними:
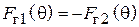 . (5.8)
. (5.8)
5.3. Обобщение на антенны с произвольно
поляризованным излучением
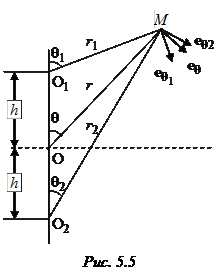 В общем случае поле излучения антенны имеет вертикальную и горизонтальную составляющие, причем каждая из них обладает своей характеристикой направленности. Полное поле каждой из антенн представляется как сумма вертикальной и горизонтальной составляющих. Запишем поле антенны 1 в произвольной точке М 1-го полупространства (рис. 5.5). Для этого сложим выражения (5.2) и (5.5), подставляя в них координаты точки М:
В общем случае поле излучения антенны имеет вертикальную и горизонтальную составляющие, причем каждая из них обладает своей характеристикой направленности. Полное поле каждой из антенн представляется как сумма вертикальной и горизонтальной составляющих. Запишем поле антенны 1 в произвольной точке М 1-го полупространства (рис. 5.5). Для этого сложим выражения (5.2) и (5.5), подставляя в них координаты точки М:
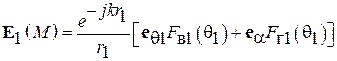 . (5.9)
. (5.9)
В той же точке М поле зеркального изображения равно
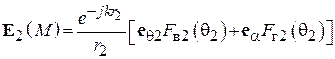 . (5.10)
. (5.10)
Если точка наблюдения находится в дальней зоне системы «антенна 1 - антенна 2», то выполняются неравенства 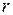 > >
> > 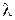 ,
, 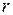 > >
> > 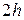 ,
, 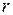 > >
> > 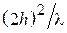 . В этом случае выражения (5.9) и (5.10) можно упростить. При выполнении указанных неравенств лучи О1 М и О2 М практически параллельны; поэтому
. В этом случае выражения (5.9) и (5.10) можно упростить. При выполнении указанных неравенств лучи О1 М и О2 М практически параллельны; поэтому 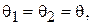
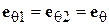 . Кроме того, в знаменателях (5.9) и (5.10) можно положить
. Кроме того, в знаменателях (5.9) и (5.10) можно положить 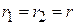 . Тогда
. Тогда
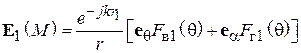 , (5.11)
, (5.11)
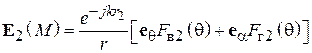 . (5.12)
. (5.12)
Наконец, примем, что характеристики направленности и по горизонтальной, и по вертикальной составляющим симметричны относительно 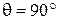 . Тогда действуют связи (5.4) и (5.8). Учитывая их, преобразуем (5.12):
. Тогда действуют связи (5.4) и (5.8). Учитывая их, преобразуем (5.12):
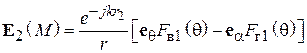
 . (5.13)
. (5.13)
Следует отметить, что поля антенн 1 и 2 из-за разницы знака при 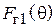 в (5.11) и (5.13) поляризованы неодинаково. Допустим, например, что
в (5.11) и (5.13) поляризованы неодинаково. Допустим, например, что 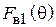 и
и 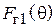 равны по модулю и сдвинуты по фазе на 90º, так что квадратную скобку в (5.11) можно записать в виде
равны по модулю и сдвинуты по фазе на 90º, так что квадратную скобку в (5.11) можно записать в виде 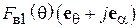 . Это означает, что поле антенны 1 имеет левую круговую поляризацию (если смотреть по направлению распространения волны). В то же время для поля антенны 2 та же скобка записывается как
. Это означает, что поле антенны 1 имеет левую круговую поляризацию (если смотреть по направлению распространения волны). В то же время для поля антенны 2 та же скобка записывается как 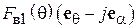 , т. е. это поле с правой круговой поляризацией.
, т. е. это поле с правой круговой поляризацией.