
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основы метода
|
|
Будем рассматривать каноническую форму задачи линейного программирования.
Приведем, прежде всего, систему ограничений к единичному базису и допустим для определенности, что этот базис состоит из первых r столбцов. Кроме того, в записи линейной функции перенесем все переменные в левую часть равенства.
Тогда задача II запишется так:
Найти решение Х системы уравнений:
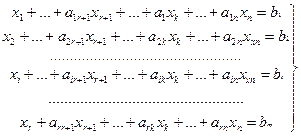 (1)
(1)
удовлетворяющее условиям неотрицательности
x1 ≥ 0; x2 ≥ 0; …, xk ≥ 0; …, xn ≥ 0; (2)
и максимизирующее линейную функцию
z — с1х1 — с2х2 —... — сkхk —... — сnхn =—с0 (3)
Допустим, что в системе (1) все свободные члены неотрицательны, т. е. выполняется неравенство bi ≥ 0, для i = 1, 2,..., r. (4)
Тогда системе (1) соответствует исходное опорное решение
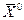 = (b1, b2... bi, 0,... 0). (5)
= (b1, b2... bi, 0,... 0). (5)
Подставляя это решение в равенство (3), вычислим соответствующее исходное значение функции z0 = z(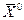 ) = с1а10 +... + сrаr0. Преобразуем функцию z так, чтобы она зависела только от свободных переменных хr+1, хr+2,..., хn.
) = с1а10 +... + сrаr0. Преобразуем функцию z так, чтобы она зависела только от свободных переменных хr+1, хr+2,..., хn.
Для этого умножим первое уравнение системы (1) на с1, второе — на с2 и т. д., r-е. уравнение — на сr, и сложим с равенством (3).
В результате получим
Z + a0r+1хr+1 + а0r+2+xr+2 +... + а0k xk+...a0n xn=а00, (6)
где b0k= 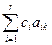 - сk (для k=r + 1, r + 2,..., n, 0). (7)
- сk (для k=r + 1, r + 2,..., n, 0). (7)
Будем называть равенство (6) приведенным (к свободным переменным) выражением для функции z, а коэффициенты а0k- — оценками соответствующих свободных переменных хk.
Способ образования приведенного выражения для функции Z остается в силе и в том случае, когда номер базисной переменной не совпадает с номером уравнения, т. е. когда, например, первое уравнение разрешено относительно х3, второе — относительно х8 и т. д.. Следует лишь в формуле (7) величины сi рассматривать не как коэффициенты при i-й переменной, а как коэффициенты в равенстве (З) при базисной переменной, относительно которой разрешено i-е уравнение. Приведенное выражение (6) позволяет сразу без дополнительных расчетов определить значение z0, соответствующее опорному решению (5): z0+z(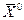 )=a00.
)=a00.
Равенство (6) формально не отличается от уравнений системы (1). Поэтому будем рассматривать его как «нулевое» уравнение, разрешенное относительно дополнительной базисной переменной z. Добавив его к системе (1), получим расширенную систему:
Заметим, что столбец свободных членов системы (8) содержит полную информацию на данном этапе расчета: первые r его членов определяют исходное опорное решение 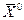 , а последний член — соответствующее значение целевой функции z0.
, а последний член — соответствующее значение целевой функции z0.
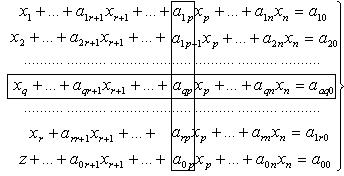
Выполним теперь одно симплексное преобразование этой системы при условии, чтобы последнее уравнение не выбиралось в качестве разрешающего (т. е. чтобы z все время оставалось в качестве базисной переменной). При выполнении этого преобразования разрешающий столбец 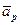 выбирался произвольно, лишь бы он содержал хотя бы один положительный элемент аip, > 0. По причинам, которые выяснятся ниже, дополним алгоритм преобразований условием выбора разрешающего столбца по отрицательной оценке а0p.
выбирался произвольно, лишь бы он содержал хотя бы один положительный элемент аip, > 0. По причинам, которые выяснятся ниже, дополним алгоритм преобразований условием выбора разрешающего столбца по отрицательной оценке а0p.
С этим дополнением алгоритм симплексных преобразований включает следующие основные пункты:
1. Выбирается разрешающий столбец аp из условий: оценка а0p < 0 и хотя бы один элемент аiр > 0. (9)
2. Выбирается разрешающая q-я строка из условия:
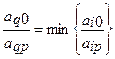 (10)
(10)
для aip> 0
З. Производится пересчет элементов разрешающей строки по формуле
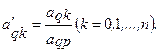 (11)
(11)
4. Вычисляются элементы всех остальных строк (при k ≠ p) по формуле
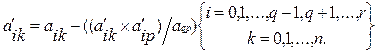 (12)
(12)
После выполнения одной итерации придем к новой системе уравнений, приведенной к новому единичному базису. Этот новый базис состоит, как и исходный, из единичных векторов 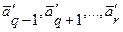 и вместо вектора
и вместо вектора 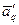 включает единичный вектор
включает единичный вектор  . Иными словами, новыми базисными переменными окажутся x1, x2, …, xq-1, xq+1, …, xr и переменная xp (заменившая переменную xq) Соответствующее преобразованной системе, новое опорное решение будет
. Иными словами, новыми базисными переменными окажутся x1, x2, …, xq-1, xq+1, …, xr и переменная xp (заменившая переменную xq) Соответствующее преобразованной системе, новое опорное решение будет
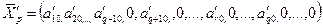 (13)
(13)
и новое значение функции z:
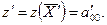 (14)
(14)
Подставляя в (14) значение а0 из (12) и вычитая из нового значения функции исходное, получим изменение функции, достигнутое в результате данной итерации,
 (15)
(15)
В этом выражении  представляет собой новый свободный член q-го (разрешающего) уравнения, которое после проведения итерации оказалось разрешенным относительно новой базисной переменной Хр. Таким образом,
представляет собой новый свободный член q-го (разрешающего) уравнения, которое после проведения итерации оказалось разрешенным относительно новой базисной переменной Хр. Таким образом,  есть значение, которое принимает эта переменная в новом опорном решении. Но в исходном опорном решении Хр, как свободная переменная, равнялась нулю, поэтому
есть значение, которое принимает эта переменная в новом опорном решении. Но в исходном опорном решении Хр, как свободная переменная, равнялась нулю, поэтому  равно изменению переменной Хр в результате ее введения в базис, т. е.
равно изменению переменной Хр в результате ее введения в базис, т. е. 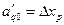
Будем полагать вначале, что ни один из свободных членов системы (1) и систем, получаемых после очередных итераций, не обращается в нуль.
Случай, когда какой-нибудь из свободных членов аi0 = 0 приводит к так называемому вырожденному решению.
Подставляя значение 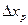 в равенство (15) и разделив на
в равенство (15) и разделив на 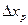 получим
получим
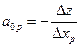 (16)
(16)
Таким образом, оценка а0р свободной переменной xр характеризует изменение целевой функции z, приходящееся на каждую единицу изменения значения переменной хр. Этим и объясняется термин “оценка”.
Так как 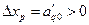 , то
, то 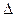 z противоположно по знаку оценке а0р. Поэтому для того чтобы функция z возрастала, т.е. чтобы новое опорное решение было “лучше” предыдущего, необходимо выбирать разрешающий столбец по отрицательной оценке.
z противоположно по знаку оценке а0р. Поэтому для того чтобы функция z возрастала, т.е. чтобы новое опорное решение было “лучше” предыдущего, необходимо выбирать разрешающий столбец по отрицательной оценке.
Этим объясняется дополнительное условие выбора разрешающего столбца, включенное в п. 1 алгоритма. Если бы решалась задача минимизации функции z, то, очевидно, разрешающий столбец следовало бы выбирать по положительной оценке а0р.