Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи теории игр
|
|
На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, т.е. возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. Такие ситуации, возникающие при игре в шахматы, шашки, домино и т.д., относятся к конфликтным: результат каждого хода игрока зависит от ответного хода противника, цель игры – выигрыш одного из партнеров. В экономике конфликтные ситуации встречаются очень часто и имеют многообразный характер. К ним относятся, например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Во всех этих примерах конфликтная ситуация порождается различием интересов партнеров и стремлением каждого из них принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера, и учитывать неизвестные заранее решения, которые эти партнеры будут принимать.
Для грамотного решения задач с конфликтными ситуациями необходимы научно обоснованные методы. Такие методы разработаны математической теорией конфликтных ситуаций, которая носит название теория игр.
Первые работы по теории игр относятся к началу ХХ века. Основателем теории игр является американский математик Дж. фон Нейман, который в 1928 году доказал основополагающую теорему теории игр – теорему о минимаксе. Бурное развитие теория игр получила после выхода в свет в 1944 году книги Дж. фон Неймана и О. Моргенштерна «Теория игр и экономическое поведение», в которой впервые было дано систематизирование электронной вычислительной техники.
Конфликтные ситуации могут возникать и во многих других областях человеческой деятельности. Это ситуации, складывающиеся при планировании и в ходе военных действий, при анализе надежности технических систем. Здесь теория игр нашла широкое применение.
В настоящее время теория игр представляет собой развитую математическую дисциплину. За последние годы были преодолены трудности, возникающие из-за сложности анализа математических моделей экономических систем методами теории игр. Созданы новые, позволяющие решать такие задачи численные методы.
Если имеется несколько конфликтующих сторон (лиц), каждая из которых принимает некоторое решение, определяемое заданным набором правил, и каждому из лиц известно возможное конечное состояние конфликтной ситуации с заранее определенными для каждой из сторон платежами, то говорят, что имеет место игра. Задача теории игр состоит в выборе такой линии поведения данного игрока, отклонение от которой может лишь уменьшить его выигрыш.
Основные понятия и определения теории игр
Ситуация называется конфликтной, если в ней участвуют стороны, интересы которых полностью или частично противоположны.
Игра — это действительный или формальный конфликт, в котором имеется по крайней мере два участника (игрока), каждый из которых стремится к достижению собственных целей.
Допустимые действия каждого из игроков, направленные на достижение некоторой цели, называются правилами игры.
Количественная оценка результатов игры называется платежом.
Игра называется парной, если в ней участвуют только две стороны (два лица).
Парная игра называется игрой с нулевой суммой, если сумма платежей равна нулю, т. е. если проигрыш одного игрока равен выигрышу второго.
Однозначное описание выбора игрока в каждой из возможных ситуаций, при которой он должен сделать личный ход, называется стратегией игрока.
Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш.
Пусть имеется два игрока, один из которых может выбрать i-ю стратегию из m своих возможных стратегий (i=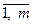 
), а второй, не зная выбора первого, выбирает j-ю стратегию из п своих возможных стратегий (j= 
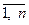). В результате первый игрок выигрывает величину аij, а второй проигрывает эту величину.
Из чисел аij составим матрицу
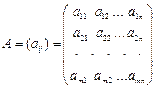
Строки матрицы A соответствуют стратегиям первого игрока, а столбцы — стратегиям второго. Эти стратегии называются чистыми.
Матрица А называется платежной (или матрицей игры).
Игру, определяемую матрицей А, имеющей m строк и n столбцов, называют конечной игрой размерности m× n.
Число α =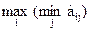 
называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) — максиминной.
Число β =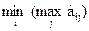 
называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) — минимаксной.
Теорема 1. Нижняя цена игры всегда не превосходит верхней цены игры.
Если α = β = υ, то число υ называется ценой игры.
Игра, для которой α = β, называется игрой с седловой точкой.
Для игры с седловой точкой нахождение решения состоит в выборе максиминной и минимаксной стратегий, которые являются оптимальными.
Если игра, заданная матрицей, не имеет седловой точки, то для нахождения ее решения используются смешанные стратегии.
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока.
Из данного определения непосредственно следует, что сумма компонент указанного вектора равна единице, а сами компоненты не отрицательны. Обычно смешанную стратегию первого игрока обозначают как вектор U = (u1, u2..., um), а второго игрока — как вектор Z = (z1, z2..., zn), где ui ≥ 0 (i= 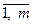), zi ≥ 0 (j= ), 
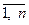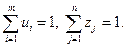
Если U * — оптимальная стратегия первого игрока, a Z * — оптимальная стратегия второго игрока, то число
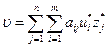
является ценой игры.
Определение оптимальных стратегий и цены игры и составляет процесс нахождения решения игры.
Теорема 2 Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях.
Теорема 3 Для того чтобы число v было ценой игры, a U* и Z* — оптимальными стратегиями, необходимо и достаточно выполнение неравенств
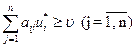и 
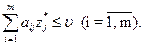
Если теорема 2 дает ответ на вопрос о существовании решения игры, то следующая теорема дает ответ на вопрос, как найти это решение для игр 2× 2, 2× n и n× 2, примеры которых приведены ниже.
Теорема 4 Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры υ вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии).
Рассмотрим примеры.
Пример1. Найти решение игры, заданной матрицей и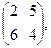 
дать геометрическую интерпретацию этого решения.
Решение. Прежде всего проверим наличие седловой точки в данной матрице. Для этого найдем минимальные элементы в каждой из строк (2 и 4) и максимальные элементы в каждом из столбцов (6 и 5). Значит, нижняя цена игры α = mах (2; 4) =4, а верхняя цена игры β = min (6; 5) = 5. Так как α = 4 ≠ β = 5, то решением игры являются смешанные оптимальные стратегии, а цена игры v заключена в пределах 4≤ υ ≤! 5.
Предположим, что для игрока А стратегия задается вектором U = (u1; u2). Тогда на основании теоремы 4 при применении игроком В чистой стратегии В1 или В2 игрок А получит средний выигрыш, равный цене игры, т. е.
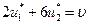(при стратегии В1),
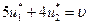(при стратегии В2).
Помимо двух записанных уравнений относительно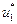 
и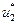 
добавим уравнение, связывающее частоты 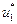и .
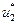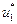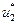+ = 1.
Решая полученную систему трех уравнений с тремя неизвестными, находим 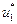=2/5; 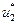=3/5; υ = 22/5.
Найдем теперь оптимальную стратегию для игрока В. Пусть стратегия для данного игрока задается вектором Z=(z1; z2).
Тогда
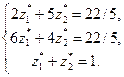
Решая систему уравнений, состоящую из каких-нибудь двух уравнений, взятых из последней системы, получим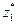 
=1/5;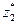 
=4/5. Следовательно, решением игры являются смешанные стратегии U* = (2/5; 3/5) и Z* = (1/5; 4/5), а цена игры υ = 22/5.
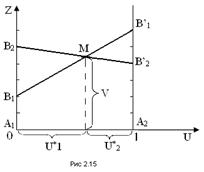
Дадим теперь геометрическую интерпретацию решения данной игры. Для этого на плоскости uOz введем систему координат и на оси Оu отложим отрезок единичной длины А1А2, каждой точке которого поставим в соответствие некоторую смешанную стратегию U= (u1, u2) = (u1, 1- u1)
(рис. 1). В частности, точке А1 (0; 1) отвечает стратегия A1, точке А2 (1; 0) —стратегия А2 и т. д.
 | |||
 | |||
|
Пример 2. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируются три возможных варианта выпуска данной модели (А, Б, В). Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль (тыс. руб.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей
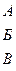
Требуется найти объем выпуска модели одежды, обеспечивающий среднюю величину прибыли при любом состоянии спроса.
Решение. Прежде всего проверим, имеет ли исходная матрица седловую точку. Для этого находим минимальные элементы в ее строках (22; 21; 20) и максимальные— в столбцах (22; 23; 24). Максимальным среди минимальных элементов строк является число а = 22, а минимальным среди максимальных элементов столбцов — число р = 22. Таким образом, а = |3 = 22. Число 22 является ценой игры. Игра имеет седловую точку, соответствующую 1 варианту выпуска модели одежды. Объем выпуска модели, соответствующей данному варианту, обеспечивает прибыль в 22 тыс. руб. при любом состоянии спроса.
Используя геометрическую интерпретацию, найдите решение игр, определяемых следующими матрицами.