
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическая часть (решение задачи ручным способом)
|
|
Задача 10 1. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице 10.2.
Таблица 10.2 – Исходные данные задачи 10.1
| Вид сырья | Нормы затрат сырья (кг) на одно изделие | Общее количество сырья (кг) | ||
| А | В | С | ||
| II | ||||
| III | ||||
| Цена одного изделия (тыс. руб.) |
Изделия А, В и С могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.
Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
Решение. Составим математическую модель задачи.
Искомый выпуск изделий А обозначим через x 1, изделий В -через x 2, изделий С - через х3. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные x1 x2, х3 должны удовлетворять следующей системе неравенств:
18 x1 + 15 x2 + 12 х3 £ 360,
6 x1 + 4 x2 + 8 х3 £ 192, (10.12)
5 x1 + 3 x2 + 3 х3 £ 180.
Общая стоимость произведенной предприятием продукции при условии выпуска х1 изделий A, х2 изделий В и х3 изделий С составляет
F = 9 x1 + 10 x2 + 16 x3 . (10.13)
По своему экономическому содержанию переменные х1, x2 и хз могут принимать только неотрицательные значения:
x1, x2, x3 ³ 0. (10.14)
Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (10.12) требуется найти такое, при котором целевая функция (10.13) принимает максимальное значение.
Запишем эту задачу в форме основной задачи линейного программирования (задача на максимум и ограничения – равенства). Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений
18 x1 + 15 x2 + 12 х3 + x4 = 360,
6 x1 + 4 x2 + 8 х3 + x5 = 192, (10.15)
5 x1 + 3 x2 + 3 х3 + x6 = 180.
Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, x 4 — это неиспользуемое количество сырья I вида.
Преобразованную систему уравнений запишем в векторной форме:
x1P1 + x2P2 + x3P3 + x4P4 + x5P5 +x6P6 = P0
где P1 = 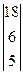 , P2 =
, P2 = 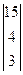 , P3 =
, P3 = 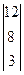 , P4 =
, P4 = 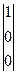 , P5 =
, P5 = 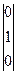 , P6 =
, P6 = 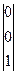 . (10.16)
. (10.16)
Поскольку среди векторов P1, Р2, Р3, P4, P5, Р6 имеются три единичных ортогональных вектора – Р4, Р5, Р6 (имеется единичный ортогональный базис, т.е. их число не меньше числа уравнений - ограничений), для данной задачи можно, используя метод единичных векторов непосредственно выбрать основные базисные переменные (остальные будут неосновными), Выразить основные переменные через неосновные, приравнять неосноые переменные 0 и записать опорный план.
Основными переменными будут х4, х5, х6 (дополнительные переменные- они кстати удовлетворяют и рассмотренному в лекции ___ правилу). Неосновными – переменные х1, х2, х3.
x4 = 360 – 18x1 – 15x2 – 12x3,
x5 = 192 – 6x1 – 42 – 8x3, (10.17)
x6 = 180 – 5x1 – 3x2 – 3x3.
Если х1 = 0, х2 = 0, х3 = 0, то из (10.17): х4 = 360, х5 = 192, х6 = 180 и начальный опорный план примет вид Х0=(0; 0; 0; 360; 192; 180), определяемый системой трехмерных единичных векторов Р4, Р5, Р6, которые образуют базис трехмерного векторного пространства.
Этот план является допустимым (значения всех переменных неотрицательные)
Составляем симплексную таблицу для 1-ой итерации (таблица 10.3).
Таблица будет иметь m + 1 = 3 + 1 = 4 строки (m – число базисных (основных) переменных) и n + 3 = 7 + 3 = 10 столбцов (n – число векторов).
Таблицу рекомендуется заполнять в следующей последовательности:
- изображаем постоянную часть таблицы (форму таблицы);
- заполняем верхнюю подстроку постоянной части таблицы (значения коэффициентов cj при переменных в целевой функции (10.13): с1 = 9, с2 = 10, с3 = 16, остальные переменные в исходную целевую функцию не входят, следовательно, коэффициенты при них равны 0;
- заполняем столбец 1 (столбец i) - (1, 2, 3, 4);
- заполняем столбец 2 (столбец «Базис) – Р4, Р5, Р6;
- заполняем столбец 3 (столбец «Сб») – это коэффициенты при основных (х4, х5, х6) переменных в целевой функции. Этих переменных в исходной целевой функции нет, следовательно, все коэффициенты при них равны 0.
- заполняем первые три строки элементами вектора Р0 (360, 192, 180);
- заполняем первые три строки элементами векторов Р1 – Р6. Обратите внимание, что коэффициенты при основных переменных (Р4, Р5, Р6) образуют единичную матрицу.
Таблица 10.3 – Симплекс таблица первой итерации задачи 10.1
| i | Базис | сб | P0 | ||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| P4 | |||||||||
| P5 | |||||||||
| P6 | |||||||||
| -9 | -10 | -16 |
Таким образом, мы, в основном, заполнили первые три строки симплекс- таблицы значениями таблицы исходных данных
Чтобы заполнить четвертую (индексную строку) необходимо произвести некоторые вычисления.
1. Вычисляем значение элемента а44 – (четвертой строки и четвертого столбца) – строка 4 столбец Р0 по формуле (10.4). По существу это значение целевой функции F0 на данном шаге. Оно равно скалярному произведению вектора Pо на вектор Сб:
F0 = 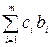 .
.
F0 = (0 * 360 + 0 * 192 + 0* 180) = 0.
2. Вычисляем значение элемента а45 (четвертой строки и пятого столбца) по формуле (10.3) а45 =  5 = z5— с5,
5 = z5— с5,
где z5 = 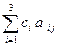 - скалярное произведение вектора С на вектор Р1.
- скалярное произведение вектора С на вектор Р1.
с5 – значение коэффициента при переменной х1 в целевой функции (записано в 5-м столбце, верхняя подстрока).
Получаем: z5 = (0 * 18 + 0 * 6 + 0 * 5) = 0,
 5 = 0 – 9 = -9 (таблица 10.3)
5 = 0 – 9 = -9 (таблица 10.3)
3. Аналогично вычисляем значения остальных элементов четвертой (индексной) строки:
z6 = (0 * 15 + 0 * 4 + 0 * 3) = 0,
 6 = 0 – 10 = -10 (таблица 10.3).
6 = 0 – 10 = -10 (таблица 10.3).
z7 = (0 * 12 + 0 * 8 + 0 * 3) = 0,
 7 = 0 – 16 = -16 (таблица 10.3).
7 = 0 – 16 = -16 (таблица 10.3).
z8 = (0 * 1 + 0 * 0 + 0 * 0) = 0,
 7 = 0 – 0 = 0 (таблица 10.3) и т.д.
7 = 0 – 0 = 0 (таблица 10.3) и т.д.
Таблица 10.3 заполнена. Получен первый опорный (допустимый) базисный план. Теперь необходимо выяснить, не является ли этот опорный план оптимальным?
Из анализа таблицы 3.10 следует, что по содержанию задачи значения всех переменных x1, х2, x3 входящих в целевую функцию с ненулевыми коэффициентамиравны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю – F0 = 0 (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.
Формально это следует и из 4-й строки таблицы 10.3, т. к. в ней имеется три отрицательных числа:  5 = - 9,
5 = - 9,  6 = - 10 и
6 = - 10 и  7 = - 16. Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.
7 = - 16. Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.
Так, число (-9) означает, что при включении в план производства одного изделия А обеспечивается увеличение выпуска продукции на 9тыс. руб. Если включить в план производства по одному изделию В и С, то общая стоимость изготовляемой продукции возрастет соответственно на 10 и 16 тыс. руб. Поэтому с содержательной экономической точки зрения наиболее целесообразным является включение в план производства изделий С. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число  j находится в 4-й строке столбца вектора Р3.
j находится в 4-й строке столбца вектора Р3.
Формально по симплекс методу такое введение в план другого изделия представляет собой введение в новый базис другого вектора (в данном случае –вектора Р3). Столбец вектора Р3 назовем направляющим.
Проверим, есть ли в этом столбце, хотя бы один элемент aij > 0? Если нет – задача не имеет решения. В данном случае есть (12, 8, 3 – все больше нуля).
Осталось решить задачу, какой вектор (соответственно, какую переменную) вывести из базиса?
Для этого по таблице 10.3 вычисляем величину отношения элементов столбца Р0 к соответствующим элементам направляющего столбца (столбца Р3), значения которых больше нуля и выделяем из них минимальное значение:
q0 = min (bi/aiНС) для аi3 > 0, т. е. q0 = min {360/12; 192/8; 180/3) = 192/8.
Вычислив число 192/8 = 24, мы тем самым с экономической точки зрения определили, какое количество изделий С предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно min (360/12; I92/8; 180/3) = 192/8 = 24, т. е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.
Отношению 192/8 = 24 в таблице 10.3 соответствует вторая строка (строка вектора Р5). Таким образом, формально, по симплекс методу, это означает, что из базиса необходимо вывести вектор Р5. Вторую строку таблицы 10.3 (строку вектора Р5) назовем направляющей строкой.
Направляющий столбец и направляющая строка в таблице 10.3 выделены красным цветом. Элемент таблицы 10.3, находящийся на пересечении направляющего столбца и направляющей строки а27 = 8 назовем разрешающим.
Составляем таблицу для II итерации (шаг 2) (таблица 10.4).
Таблица создается в той же последовательности, что и таблица 10.3 с некоторыми изменениями.
Создаем форму таблицы. Заполняем верхнюю и нижнюю подстроку. Заполняем первый столбец (все эти три пункта выполняются как в таблице 10.3 – без изменения).
Заполняем столбец 2 (здесь вместо вектора Р5 записываем вектор Р3).
Заполняем столбец 3. Здесь значение сб для вектора Р3 равно 16 (это коэффициент при переменной х3 в целевой функции).
Заполняем элементы столбцов нового базиса (Р4, Р3, Р6) – на пересечении строки и столбца с одинаковым индексом записывается 1, в остальные - 0. Например, для вектора Р4: - в первую строку (строка вектора Р4) записываем 1, в остальные 0.
Далее заполняем свободные элементы направляющей строки новой таблицы –таблицы 10.4). Значение этих элементов строки получаются из значений соответствующих элементов старой таблицы (таблицы 10.3) путем деления их на значение разрешающего элемента а27 = 8: в столбце Р0 - 192/8 = 24; в столбце Р1 - 6/8 = ¾; в столбце Р2 - 4/8 = 1/2; в столбце Р5 – 1/8.
Таблица 10.4 – Симплекс - таблица решения задачи 10. 1 (шаг 2)
| i | Базис | сб | P0 | ||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| P4 | -3/2 | ||||||||
| P3 | 3/4 | 1/2 | 1/8 | ||||||
| P6 | 11/4 | 3/2 | -3/8 | ||||||
| -2 |
Для определения остальных элементов таблицы 10.4 применяем правило треугольника. Эти элементы могут быть вычислены и непосредственно по рекуррентным формулам.
Вычислим элементы таблицы 10.4, входящие в столбец вектора Ро.
Первый из них находится в 1-й строке этого столбца. Для его вычисления используем три числа:
1) число, записанное в старой таблице 10.3 на пересечении столбца вектора Р0 и1-й строки (значение такого же элемента в старой таблице - 360;
2) число, записанное в старой таблице 10.3 на пересечении столбца вектора Рз (вновь введенного вектора) и 1-й строки (элемент корой заполняем -12);
3) число, записанное в новой таблице (10.4) на пересечении столбца вектора Р0 и 2-й строки (направляющей стоки -24).
Вычитая из первого числа произведение двух других, получаем искомый элемент: 360 - 12*24 = 72. Записываем его в 1-й строке столбца вектора P0 новой таблицы 10.4.
Второй элемент столбца вектора Ро таблицы 10.4 уже вычислен.
Для вычисления значения третьего элемента столбца вектора Р0 также используем три числа. Первое из них (180) находится на пересечении 3-й строки и столбца вектора Ро старой таблицы 10.3, второе (3) — на пересечении 3-й строки и столбца вектора Рз старой таблицы 10.3, третье (24) - на пересечении 2-й строки и столбца вектора Ро новой таблицы 10.4. Итак, указанный элемент есть 180 – 24*3 = 108. Число 108 записываем в 3-й строке столбца вектора Ро новой таблицы 10.4.
При определении по правилу треугольника элементов столбца вектора Р0 третье число, стоящее в нижней вершине треугольника, все время оставалось неизменным и менялись лишь первые два числа. Учтем это при вычислении элементов столбцов векторов P1, Р2, Р5 новой таблицы 10.4.
Для вычисления указанных элементов первые два числа берем из столбцов векторов Р1и Р3 старой таблицы 10.3, а третье число - из новой таблицы 10.4.
Покажем это на примере вычисления элемента а15 (первая строка вектора Р1): значение вычисляемого элемента а15 в старой таблице (18) минус произведение значения элемента первой строки направляющего столбца старой таблицы (а17 = 12) на уже рассчитанное значение элемента, находящегося на пересечении направляющей строки и данного рассчитываемого вектора (в данном случае вектора Р1 ) новой таблицы – а25 = ¾., т.е. 18 -12*(3/4) = 9. Аналогично для элемента а35 новой таблицы: значение элемента а35 старой таблицы (5) минус произведение а33 = 3 старой таблицы на уже рассчитанное значение элемента, находящегося на пересечении направляющей строки и данного рассчитываемого вектора (в данном случае вектора Р1 ) новой таблицы – а25 = ¾., т.е. 5-3*(3/4) =11/4.
Аналогично вычисляем элементы столбца вектора Р2:
а16Н = а16С – а17С * а26Н = 15 – 12 * ½ = 9;
а26Н - уже рассчитан;
а36Н = а36С - а37С * а26Н = 3 – 3 * ½ = 3/2.
Элементы столбца вектора Р3 заполнены.
Вычисляем элементы столбца вектора Р5 (по правилу треугольника):
а19Н = а19С – а17С * а29Н = 0 – 12 * 1/8 = -3/2;
а29Н – заполнен;
а39Н = а39С – а37С * а29Н = 0 – 3 * 1/8 = -3/8.
По окончании расчета всех элементов первых трех строк новой таблицы 10.4 необходимо рассчитать значения элементов четвертой (индексной) строки (по тем же формулам, что и в таблице 10.3):
- элемент а44 = F1 = 0 * 72 + 16 *24 = 0 * 108 = 384 (новое значение целевой функции, прирост 384 – 0 = 384);
- элемент а45 = (0 * 9 + 16* ¾ + 0 * 11/4) – 9 = 3;
- элемент а46 = (0 * 9 + 16 * ½ + 0 * 3/2) – 10 = -2;
- элементы а47 и а48 – заполнены;
- элемент а49 = (0 * (-3/2) + 16 * (1/8) + 0 * (-3/8) – 0 = 2;
- элемент а410 – заполнен.
Все элементы таблицы 1-.4 заполнены.
В результате анализа элементов новой таблицы 10.4 можно сделать следующие выводы.
1. Новым опорным планом задачи является план Х1 =(0; 0; 24; 72; 0; 108). При данном плане производства изготовляется 24 изделия С и остается неиспользованным 72 кг сырья 1 вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 тыс.руб. Указанные числа записаны в столбце вектора Ро таблицы 10.4. Данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели значительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным.
Так, например, рассмотрим данные столбца вектора Р2. Число 1/2 во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий С, если запланировать выпуск одного изделия В. Числа 9 и 3/2 в 1-й и 3-й строках вектора Р2 показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия В, а число (- 2) в 4-й строке показывает, что если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 тыс.руб. Иными словами, если включить в план производства продукции одно изделие В, то это потребует уменьшения выпуска изделия С на 1/2 ед. и потребует дополнительных затрат 9 кг сырья I вида и 3/2 кг сырья III вида. Общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 тыс. руб. Таким образом, числа 9 и 3/2 выступают новыми «нормами» затрат сырья I и III вида на изготовление одного изделия В (как следует из таблицы 10.3, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий С.
Такой же экономический смысл имеют и данные столбца вектора P1 таблицы 10.4. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора Р5. Число 1/8 во 2-й строке этого столбца, показывает, что увеличение объемов сырья II вида на 1 кг позволило бы увеличить выпуск изделий С на 1/8 ед. Одновременно потребовалось бы дополнительно 3/2 кг сырья I вида и 3/8 кг сырья III вида. Увеличение выпуска изделий С на 1/8 ед. приведет к росту выпуска продукции на 2 тыс. руб.
2. Из экономического содержания данных таблицы 10.4 следует, что полученный на II итерации план задачи не является оптимальным. Формально это следует и из анализа элементов 4-й строки таблицы 10.4, поскольку в столбце вектора Р2 этой строки записано отрицательное число (-2).
3. Наличие в таблице 10.4 единственного отрицательного значения ∆ 2 = (-2) формально означает, что в базис следует ввести вектор Р2, т. е. в новом плане следует предусмотреть выпуск изделий В. Столбец вектора Р2 таблицы 10.4 становится направляющим. Проверяем, есть ли в этом столбце положительные коэффициенты aij? Да есть и таких элементов три: 9, 1/2, 3/2.
Таким образом, улучшение полученного опорного плана возможно.
При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется отношением min (biН/ai2Н) для всех ai2Н> 0, т. е. вычисляем min { 72: 9; 24: (1/2); 108: (3/2)} = 8, что соответствует первой строке таблицы 10.4. Таким образом, из базиса необходимо вывести вектор Р4. Первая строка таблицы 1-.4 становится направляющей, а элемент а16 = 9 – разрешающим.
Следовательно, исключению из базиса подлежит вектор Р4, иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий В.
Шаг 3. Составляем таблицу для III итерации (таблица 10.5).
Элементы таблицы 10.5 рассчитываются по той же методике, что и для таблицы 10.4.
Таблица 10.5 – Результаты вычислений на шаге 2
| i | Базис | сб | P0 | ||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| P2 | 1/9 | -1/6 | |||||||
| P3 | 1/4 | -1/18 | 5/24 | ||||||
| P6 | 5/4 | -1/6 | -1/8 | ||||||
| 2/9 | 5/3 |
Из анализа элементов таблицы 10.5 следует:
- новый опорный план Х 2 = (0; 8; 20; 0; 0; 96);
- данный план является оптимальным, т.к. в четверной (индексной) строке нет ни одного значения  j < 0;
j < 0;
- значение целевой функции F2 при этом оптимальном плане максимально возможно и равно 400 тыс. руб..
Таким образом, план выпуска продукции, включающий изготовление 0 изделий А, 8 изделий В, 20 изделий С, является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.
Этим планом производства продукции не предусматривается изготовление изделий А. Введение в план выпуска продукции изделий вида А привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора P1, где число 5 показывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению общей величины стоимости на 5 тыс. руб.
Отметим, что решение задачи линейного программирования методом симплекс-таблиц можно проводить, используя лишь одну (обобщенную) таблицу (для данной задачи таблицу 10.6). Это существенно повышает наглядность использования данного метода, но не меняет его существа.
Таблица 10.6 – Обобщенная симплекс – таблица решения задачи 10.1
| i | Базис | сб | P0 | ||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| P4 | |||||||||
| P5 | |||||||||
| P6 | |||||||||
| -9 | -10 | -16 | |||||||
| P4 | -3/2 | ||||||||
| P3 | 3/4 | 1/2 | 1/8 | ||||||
| P6 | 11/4 | 3/2 | -3/8 | ||||||
| -2 | |||||||||
| P2 | 1/9 | -1/6 | |||||||
| P3 | 1/4 | -1/18 | 5/24 | ||||||
| P6 | 5/4 | -1/6 | -1/8 | ||||||
| 2/9 | 5/3 |
Задача решена.
* * *