Матричное представление графов

В теории графов классическим способом их представления являются матрицы инцидентности. Если в графе G=(V, W) ½ v ½ =n, ½ w½ =m, то матрица инцидентности этого графа имеет размер n´ m. Для орграфа столбец, соответствующий ориентированной дуге (x, y) содержит 1 в строке, соответствующей вершине x, -1 - в строке, соответствующей вершине y, и 0 – в остальных случаях.

Для неориентированного графа столбец, соответствующий ветви (x, y), содержит 1 в строках, отвечающих вершинам x и y, и 0 – в остальных строках. Проще говоря, если вершина x_j – начало дуги, то 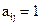; если y_j – конец дуги, то 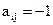; если дуга есть петля, а x_j – инцидентная ей вершина, та 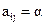, где 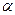- любое число, отличное от 0, -1, и 1; в остальных случаях 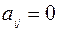(в нашем примере петель нет).

С алгоритмической точки зрения и с точки зрения памяти ЭВМ матрица инциденций графа оказывается не самой удачной и недостаточно экономной.

Во-первых, эта матрица требует n´ m ячеек памяти, причем большинство ячеек занято нулями. Неудобен также и доступ к информации. Например, ответ на вопрос: существует ли дуга (x, y)? – требует в худшем случае m шагов программы (то есть перебора всех столбцов).

Лучшим и более эффективным способом представления графа является матрица смежности (связности), определяемая как матрица 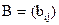размером n´ n, где 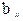=1, если существует ребро, ведущее из вершины i в вершину j и 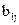= 0 в противном случае. При этом матрица неориентированного графа – симметрична. Основным преимуществом матрицы смежности является тот факт, что за один шаг можно узнать, существует ли ребро, связывающее вершину x с вершиной y. Недостатком же является то, что независимо от числа ребер объем занимаемой памяти равен n² ячеек.

Задачи

1.1. Для заданных ниже геометрическим способом графов выполнить следующие задания:

1) пометить вершины и ребра (дуги) графа буквами или цифрами;

2) определить, к какому типу относится данный граф, и привести его характеристики (степени его вершин, выделить кратные и параллельные ребра, петли, указать циклы и т.д.);

3) записать для данных графов матрицы инцидентности и матрицы смежности.

А)

б)

в)

г)

е)

1.2. Граф G = (V, E) задан либо своей матрицей инцидентности A (G), либо матрицей смежности B (G). Изобразить эти графы рисунками.

а)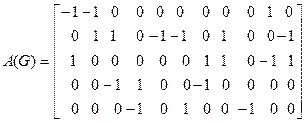

б)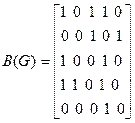

в)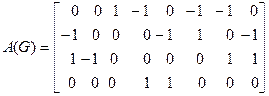

г)