Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Атака на основе Китайской теоремы об остатках.
|
|
Как отмечалось ранее, системы шифрования с открытыми ключами работают сравнительно медленно. Для повышения скорости шифрования RSA на практике используют малую экспоненту зашифрования.
Если выбрать число е небольшим или таким, чтобы в его двоичной записи было мало единиц, то процедуру шифрования можно значительно ускорить. Например, выбрав е = 3 (при этом ни р – 1, ни q – 1 не должны делиться на 3), мы сможем реализовать шифрование с помощью одного возведения в квадрат по модулю N и одного перемножения. Выбрав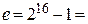 
65 537 – число, двоичная запись которого содержит только две единицы, мы сможем реализовать шифрование с помощью 16 возведений в квадрат по модулю N и одного перемножения. Если экспонента е выбирается случайно, то реализация шифрования по алгоритму RSA потребует s возведений в квадрат по модулю N и в среднем s /2 умножений по тому же модулю, где 5 – длина двоичной записи числа N. Вместе с тем выбор небольшой экспоненты е может привести к негативным последствиям. Дело в том, что у нескольких корреспондентов могут оказаться одинаковые экспоненты е.
Пусть, например, три корреспондента имеют попарно взаимно простые модули N 1, N 2, N 3 и общую экспоненту е = 3. Если еще один пользователь посылает им некое циркулярное сообщение x, то криптоаналитик противника может получить в свое распоряжение три шифрованных текста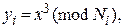 
i = 1, 2, 3. Далее он может найти решение системы сравнений, лежащее в интервале 0 < y < N 1∙ N 2∙ N 3
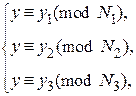
По китайской теореме об остатках такое решение единственно, а так как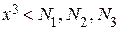 
, то y = x 3. Значение х можно найти, вычислив кубический корень 
.
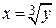Отметим, что выбор малой экспоненты расшифрования d также нежелателен в связи с возможностью определения d простым перебором. Известно также что если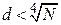 
, то экспоненту d легко найти, используя непрерывные дроби.
Пример 8. Три пользователя имеют модули N 1 = 26549, N 2 = 45901,
N 3 = 25351. Все пользователи используют экспоненту e = 3. Всем пользователям было послано некое сообщение x, причем пользователи получили сообщения y 1 = 5366, y 2 = 814, y 3 = 4454. Найдем M 0 = N 1∙ N 2∙ N 3 = 30893378827799. Далее находим
m 1 = N 2∙ N 3 = 1163636251
m 2 = N 1∙ N 3 = 673043699
m 3 = N 1∙ N 2 = 1218625649
n 1 = m 1-1 mod N 1 = 13533
n 2 = m 2-1 mod N 2 = 27930
n 3 = m 3-1 mod N 3 = 22354
S = y 1∙ n 1∙ m 1 + y 2∙ n 2∙ m 2 + y 3∙ n 3∙ m 3 = 84501028038745578 + 15301661957638980 + + 121332116653000684 = 221134806649385242
S mod M 0 = 1000000000
x = (S mod M 0)1/3 = 1000 – исходное сообщение, отправленное пользователям.