Метод проекции

Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.

Известны два метода проецирования: центральное и параллельное.

Центральное проецирование заключается в проведении через каждую точку (А, В, С, …) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, > … — проецирующего луча).

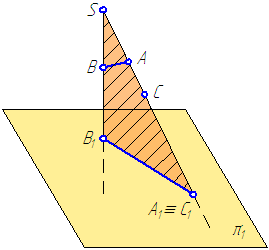
Рисунок 1.1 – Центральное проецирование

Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.

Свойство 1. Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.

Докажем это утверждение.

На рисунке 1.1: точка А ₁ – центральная проекция точки А на плоскости проекций π ₁. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С. Центральная проекция точки С (С ₁) на плоскости проекций π ₁ совпадает с проекцией точки А (А ₁):

1. С ∈ SA;

2. SC ∩ π ₁= C ₁ → C ₁ ≡ A ₁.

Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.

Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым, введём еще одну плоскость проекций (π ₂) и ещё один центр проецирования (S ₂) (Рисунок 1.2).

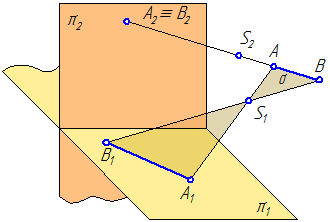
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств

Построим проекции точки А на плоскости проекций π ₂. Из всех точек пространства только точка А имеет своими проекциями А ₁ на плоскость π ₁ и А ₂ на π ₂ одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В).

Свойство 2. Проекция прямой есть прямая.

Докажем данное свойство.

Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ, задающий прямую. Треугольник Δ SAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ ∩ π ₁= А ₁ В ₁, где А ₁ В ₁ – центральная проекция прямой, заданной отрезком АВ.

Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.