переменных

Будем использовать здесь привычные в геометрии обозначения переменных: х - абсцисса, у - ордината, z - аппликата.

Дадим геометрическую интерпретацию частных производных функции

z = f(x; y). Положив y = y₀, мы получаем функцию z = f(x; y₀), график которой есть линия (L) пересечения поверхности z = f(x; y) с плоскостью y = y₀.

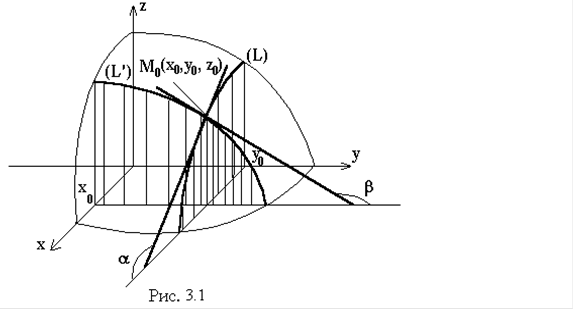
Частная производная

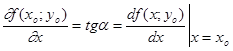равна тангенсу угла a наклона касательной к кривой (L) в точке М₀(x₀; y₀; z₀), который она образует с положительным направлением оси Ох.

Аналогично, частная производная

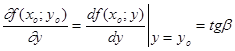равна тангенсу угла b наклона касательной к кривой (L¢): z = f(x₀; y) в точке М₀(x₀; y₀; z₀), который она образует с положительным направлением оси Оy.

Касательная плоскость и нормаль к поверхности.

Рассмотрим поверхность, заданную уравнением F(x; y; z)=0, причем F(x; y; z) будем считать дифференцируемой функцией.

Выберем на поверхности точку М₀(x₀; y₀; z₀) и проведем через нее какую-нибудь линию (L), целиком лежащую на поверхности. Пусть эта линия описывается уравнениями:

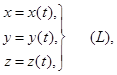
где x(t), y(t), z(t) - дифференцируемые функции по t, причем:

Каждая точка кривой L лежит на поверхности, поэтому   x 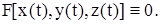F y t z Продифференцируем обе части тождества по t: 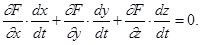Полученное равенство справедливо и в точке М0 (при t = to):

(4)

Рассмотрим 2 вектора:

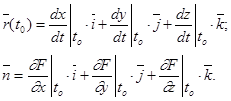
Из равенства (4) следует, что .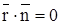

Пусть 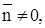тогда 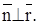Но вектор 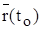- касательный к кривой L. Так как кривая L проведена через М₀ произвольно, то таких векторов 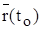можно получить множество, проводя через М₀ различные кривые L на поверхности. Все эти векторы перпендикулярны вектору , следовательно, все они лежат в одной плоскости, называемой касательной плоскостью; чтобы составить ее уравнение, примем вектор в качестве нормального вектора касательной плоскости, проходящей через М₀.

Тогда ее уравнение будет иметь вид:

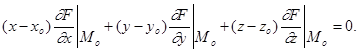
Уравнение нормали (прямой, перпендикулярной касательной плоскости и проходящей через М₀(x₀; y₀; z₀) получим, приняв за направляющий вектор . Тогда 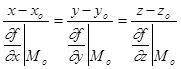- уравнение нормали к поверхности

F(x; y; z) = 0 в точке М₀.

1.11. Частные производные и полные дифференциалы высших порядков

Для простоты записей будем рассматривать функции двух переменных

y = f(x₁, x₂).

Мы отмечали ранее, что частные производные и полный дифференциал можно рассматривать как функции переменных х₁, х₂. Следовательно, для этих функций можно ставить вопрос о вычислении частных производных и полных дифференциалов.

Частной производной второго порядка называют частную производную от частной производной. При этом возможны следующие ситуации:

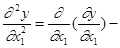вторая частная производная дважды по х₁;

вторая частная смешанная производная по х₁ и по х₂;

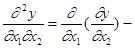вторая частная смешанная производная по х₂ и по х₁;

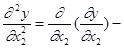вторая частная производная дважды по х₂.

Аналогичным образом определяются частные производные более высоких порядков. Вообще, частная производная порядка n есть частная производная от частной производной порядка (n - 1). Например,

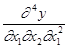означает следующее:

где .

Вообще говоря, даже смешанные частные производные второго порядка 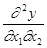и 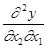различны.

Однако имеет место следующая теорема.

Теорема. Есл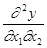и и 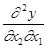непрерывны на множестве, то они совпадают.

Аналогичное утверждение справедливо для любых других смешанных частных производных.

Полным дифференциалом второго порядка называют полный дифференциал от полного дифференциала: d²y = d(dy). Вообще, полным дифференциалом порядка n называют полный дифференциал от полного дифференциала порядка (n - 1): dⁿy = d(d^{n -1}y).

Пользуясь формулой (3), получаем:

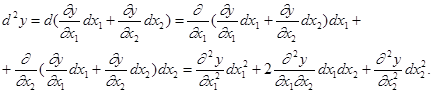
В символической форме это равенство можно записать в виде:

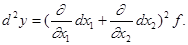
Методом математической индукции нетрудно убедиться в том, что

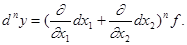
3.2. Экстремумы функций нескольких переменных

Пусть точка а = (а₁, а₂,..., а_n) - внутренняя точка области определения функции y = f(x), x = (x₁, x₂,..., x_n).

Определение. Мы будем говорить, что в точке а функция y = f(x) имеет максимум (минимум), если в достаточно малой окрестности точки а c выколотым центром имеет место неравенство:

f(x) < f(a) (f(x) > f(a)).

Обе определенные ситуации «минимум и максимум» объединяются термином «экстремум».

Рассмотрим вместе с функцией f(x) n порождаемых ею функций одного переменного:

y_j(x_j) = f(a₁, a₂,..., a_j-1, x_j, a_j+1,..., a_n), где j = 1, 2,..., n.

Из определения вытекает, что функция одного переменного y_j(x_j) имеет в точках a_j, j = 1, 2,..., n, такой же экстремум, как и функция f(x) в точке а. Кроме того, по определению производных.

Вспоминая необходимые условия экстремума для функции одного переменного, приходим к следующему утверждению.

2.1. Необходимые условия экстремума

Если функция y = f(x₁, x₂,..., x_n) имеет в точке а = (а₁, а₂,..., а_n) экстремум и частные производные, то:

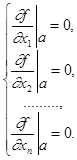
Следствие. Функция нескольких переменных может иметь экстремум лишь в тех точках, где частные производные либо обращаются в нуль, либо не существуют.

Точки, в которых частные производные функции y = f(x) либо обращаются в нуль, либо не существуют, называются критическими точками функции.

Итак, функция может иметь экстремум лишь в критической точке. Однако не всякая критическая точка есть точка экстремума. Например, для функции 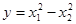точка (0, 0) очевидно, является критической. Но эта точка не является точкой экстремума, ибо в любой окрестности этой точки:

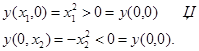
Приведенный пример является “историческим” в следующем смысле. Поверхность напоминает в точке (0. 0) седло. В связи с этим критические точки функции, не являющиеся точками экстремума, принято называть седловыми точками.

2.2. Достаточные условия экстремума

Вопрос о достаточных условиях экстремума для функций нескольких переменных сложен. Поэтому мы приведем без доказательства достаточные условия экстремума для функции двух переменных.

Теорема. Пусть в критической точке а = (a₁, a₂) функция y = f(x₁, x₂) имеет частные производные второго порядка. Положим:

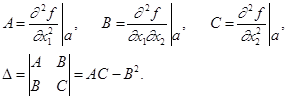
Тогда возможны следующие ситуации:

а) при D > 0, А < 0 функция имеет максимум в точке а;

б) при D > 0, А > 0 функция имеет минимум в точке а;

в) при D < 0 экстремума в точке а нет (точка а - седловая);

г) при D = 0 для исследования нужно привлекать производные более высоких порядков.

3.2.3. Понятие о методе наименьших квадратов

Во многих задачах практики требуется по результатам наблюдений двух величин

установить аналитическую зависимость между ними хотя бы приближенно. Один из подходов при решении этой задачи состоит в следующем.

Задаются видом зависимости y = f(x, a, b, c,...), где a, b, c,... - параметры. Эти параметры требуется подобрать так, чтобы расстояние r между экспериментальными значениями функции y_э = (y₁, y₂,..., y_n) и расчетными значениями y_p = (f(x, a, b,...), f(x₂, a, b,...),...., f(x_n, a, b,...)) было минимальным.

Таким образом, требуется подобрать a, b, c,... так, чтобы r(y_э, y_p) было минимальным.

Удобнее технически оказалось минимизировать функцию S= r²(y_э, y_p),

что, как легко видеть, приводит к одному и тому же результату.

Итак, требуется исследовать функцию

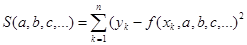на минимум.

Легко понять, что сумма квадратов (что очевидно геометрически при n = 1, 2) может иметь лишь минимум. В силу этого достаточно составить систему нормальных уравнений:

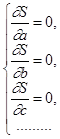
и, решив ее, определить нужные значения параметров.

Реализуем описанную схему, предполагая, что искомая зависимость линейна, т.е. y = ax + b. В таком случае имеем:

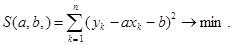
Составив систему нормальных уравнений

после упрощений получаем:

Решая полученную систему, например, по формулам Крамера, получим: