
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм умножения
|
|
ЛАБОРАТОРНАЯ РАБОТА № 3-1
ТЕМА РАБОТЫ: МАШИННЫЕ АЛГОРИТМЫ УМНОЖЕНИЯ
Цель работы
В результате выполнения лабораторной работы:
1.1. Уметь реализовывать машинные алгоритмы умножения целых чисел.
Материал для предварительного изучения
2.1. Линейные и циклические сдвиги, поразрядные операции
2.2. Перевод целых чисел из 10-й системы счисления в 2-ю и наоборот
Задание к лабораторной работе
3.1. Выбрать вариант задания из табл. 5.1 по своему номеру в журнале группы.
3.2. Представить полученные двоичные числа в формате с фиксированной точкой X2 и Y2 в прямом (ПК) и дополнительном кодах (ДК).
3.3. Выполнить вручную умножение двоичных чисел X2 и Y2. Использовать при сложении различные комбинации знаков исходных чисел: (+X2+Y2); ((–X2)+(–Y2)); (+X2+(–Y2)); ((–X2)+Y2).
3.4. Запустить программу lab5_ORK_06.exe, либо просмотрите и запустите на выполнение файл lab5_ORK_06.pas в среде Borland Pascal. Доказать корректность реализованного алгоритма умножения.
3.5. Оформить отчет о работе.
алгоритм умножения
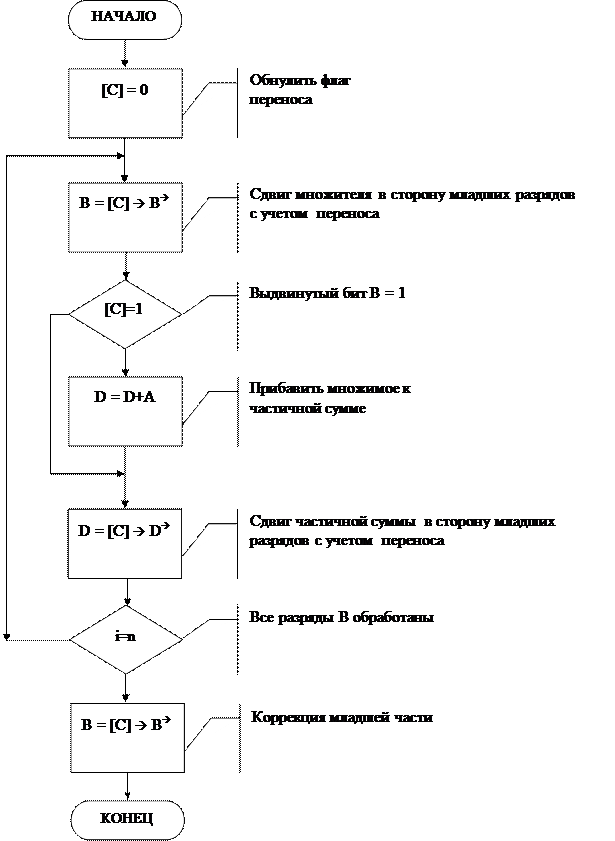
Реализация команды умножения чисел проводится путем пошагового сложения сдвигаемого значения множимого и частичной суммы при наличии ненулевого бита соответствующего разряда множителя.
Изучаемый в данной лабораторной работе алгоритм характеризуется тем, что для множимого, множителя и частичной суммы используются регистры одной величины. Результат (произведение) при этом хранится в паре, соответствующей частичной сумме и множителя, которое постепенно заполняется нулями, при чем старшая часть хранится в регистре частичной суммы, а младшая - в регистре множителя.
1. Сдвиг множителя на 1 разряд в сторону младших разрядов с учетом переноса предыдущих сдвигов, т.е.SHR.
2. Если выдвинутый бит не равен «1», то перейти к 4-му пункту.
3. Добавить множимое к частичной сумме.
4. Сдвиг частичной суммы на 1 разряд в сторону младших разрядов, используя флаг переноса в качестве старшего разряда, т.е. RCR.
5. Если количество циклов не равно N+1, то перейти на пункт 1.
6. Восстановление значения частичной суммы путем сдвига ее на один разряд в сторону старших разрядов с учетом ранее выдвинутого бита, т.е.SHL.
Произведение хранится в паре «частичная сумма: множитель». Регистр частичной суммы - старшая часть результата, регистр множителя - младшая часть.
Пусть А – множимое, В – множитель, D – частичная сумма.
 |
Пример 4.1: Пусть A = 610 = 01102 (множимое);
B = 310 = 00112 (множитель);
D = 00002 (частичная сумма)
| № такта | Действие | Флаг [C] | ||

| ||||
| Сдвиг В вправо | B = [0]001|1 | |||
| [C] = 1, след. прибавляем множимое к частичной сумме | D = D + A
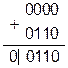
| |||
| Сдвиг D вправо | D = [0]011|0 | |||
| Сдвиг В вправо | B = [0]000|1 | |||
| [C] = 1, след. прибавляем множимое к частичной сумме | D = D + A
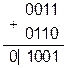
| |||
| Сдвиг D вправо | D = [0]100|1 | |||
| Сдвиг В вправо | B = [1]000|0 | |||
| Сдвиг D вправо | D = [0]010|0 | |||
| Сдвиг В вправо | B = [0]100|0 | |||
| Сдвиг D вправо |  D = [0]001|0 D = [0]001|0
| |||
| Сдвиг В вправо | B = [0]010|0 | |||
| Сдвиг D вправо | D = [0]000|1 | |||
| Сдвиг D влево | D = 0|000[1] |
Результат D, B: 0001, 0010. 000100102 = 1810.
При умножении чисел в прямых кодах знаковые и информационные разряды обрабатываются раздельно. Для определения знака результата производится суммирование цифр, записанных в знаковых разрядах операндов.
Если множитель является отрицательным числом, то умножение чисел проводят в дополнительном коде по аналогичному алгоритму умножения чисел в прямом коде, но знак результата получается автоматически. При этом при умножении множимого А на знаковую единицу множителя В необходимо просуммировать не А, а [ –А ]дк. Если множимое является отрицательным числом, то в сложении участвуют 1, полученные за счет дописывания слева перед множимым незначащих нулей и последующей инверсией.
Пример 4.2: Пусть A = 1010 = 0 01102 (множимое); [ А] дк = 0 1010
B = -1310 = 1 11012 (множитель); [ В] дк = 1 0011
10011
01010 1
01010 1
00000 0
00000 0
1 0110 1
1 01111110
При умножении на знаковую единицу множителя В была сделана коррекция – подставлено и просуммировано [– А] дк = 1 0110.
Так как в знаковом разряде произведения стоит 1, то это означает, что результат умножения получен в дополнительном коде. Для перехода в прямой код произведение надо проинвертировать и прибавить 1 к младшему разряду: 1 10000001+1= 1 10000010.
Результат:
D =1 100000102 = –(1*27+0*26+0*25+0*24+0*23+0*22+1*21+0*20 ) = –(128+2) =–13010.
Пример 4.3: Пусть A = -1010 (множимое); [ А] дк = 1 0110.
B = 1310 (множитель); [ В] дк = 0 1101
1 0110
0 1101
111110110 1
00000000 0
1110110 1
110110 1
00000 0
Так как множимое является отрицательным числом, то при сложении используются единицы множимого, полученные путем инверсии незначащих нулей старших разрядов, при наличии ненулевого бита множителя. В знаковом разряде произведения стоит 1, то это означает, что результат умножения получен в дополнительном коде.
Для перехода в прямой код произведение надо проинвертировать и прибавить 1 к младшему разряду: 1 10000001+1= 1 10000010.
Результат:
D =1 100000102 = –(1*27+0*26+0*25+0*24+0*23+0*22+1*21+0*20) = –(128+2) = –13010.
Табл.5.1. Индивидуальное задание
| Вариант | Множимое – А10 | Множитель – В 10 | Вариант | Множимое – А10 | Множитель – В 10 |
| –36 | –27 | ||||
| –5 | |||||
| –25 | |||||
| –4 | |||||
| –36 | –26 | ||||
| –32 | –10 | –17 | |||
| –15 | –19 | ||||
| –35 | –8 | –5 | |||
| –19 | |||||
| –7 | –5 | ||||
| –5 | –12 | ||||
| –8 | –7 |
СОДЕРЖАНИЕ ОТЧЕТА
1) Номер лабораторной работы.
2) Тема лабораторной работы
3) Цель лабораторной работы.
4) Индивидуальное задание.
5) Ход выполнения лабораторной работы
6) Результат выполнения лабораторной работы.
7) Выводы.
Отчет выполняется на украинском языке.
|