
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример решения задачи нейро-нечеткого вывода
|
|
Для иллюстрации процесса разработки гибридной сети в системе MATLAB рассмотрим задачу построения адаптивной системы нейро-нечеткого вывода для аппроксимации некоторой зависимости, которая описывается математической функцией у=х3. Этот пример позволяет не только уточнить содержание и последовательность этапов разработки, но и оценить точность полученной нечеткой модели посредством сравнения прогнозируемых модельных значений с известными заранее значениями соответствующей функции.
Общая последовательность процесса разработки модели гибридной сети может быть представлена в следующем виде.
1. Для начала с помощью скрипта в рабочей памяти matlab создадим обучающий массив пар " значение входной переменной — значение выходной переменной".
x = 10.*rand(20, 1);
y=x.^3;
T=[x y];
2.Далее загрузим обучающие данные в редактор ANFIS. В рабочем окне редактора будет изображен график, форма которого аналогична исходной математической функции.
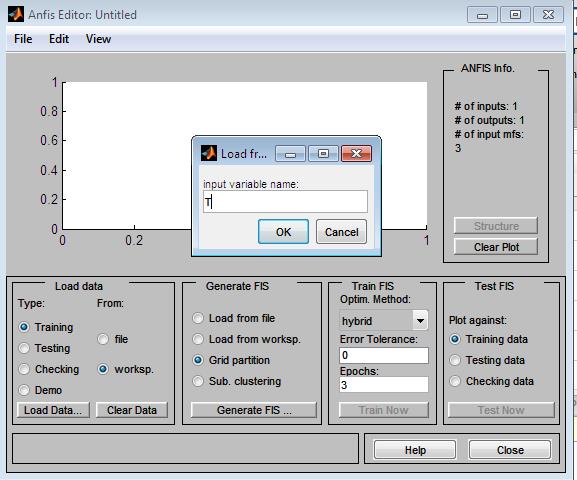
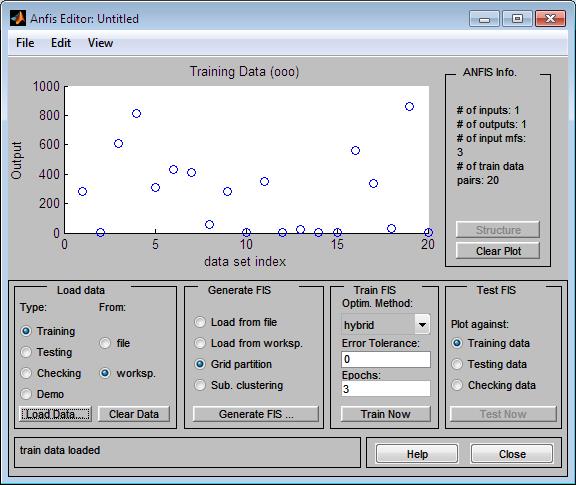
3.Далее можно приступить к генерации структуры системы нечеткого вывода FIS. Установив параметры генерации,
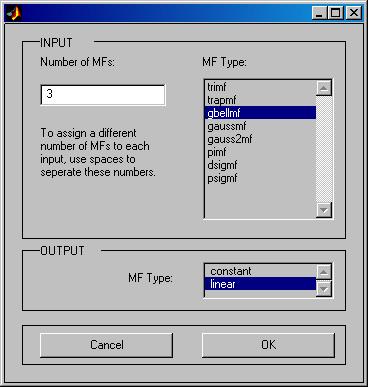
получим структуру FIS.
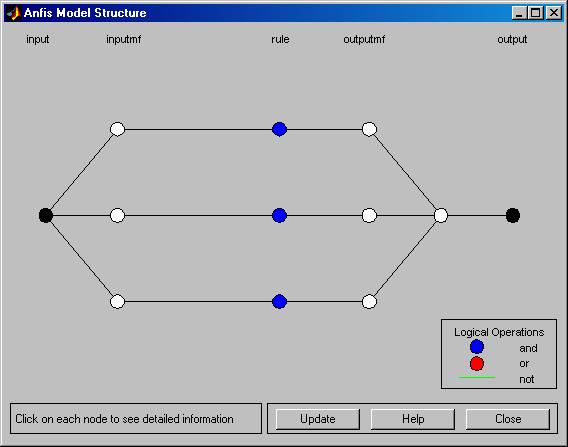
4. Теперь можно перейти к обучению сгенерированной системы нечеткого вывода. Для этого оставим без изменения предложенные системой MATLAB по умолчанию метод обучения (гибридный) и уровень ошибки (0), а количество циклов обучения изменим на 40. После обучения сети в рабочем окне редактора ANFIS будет изображен график изменения ошибки в ходе выполнения отдельных циклов обучения.
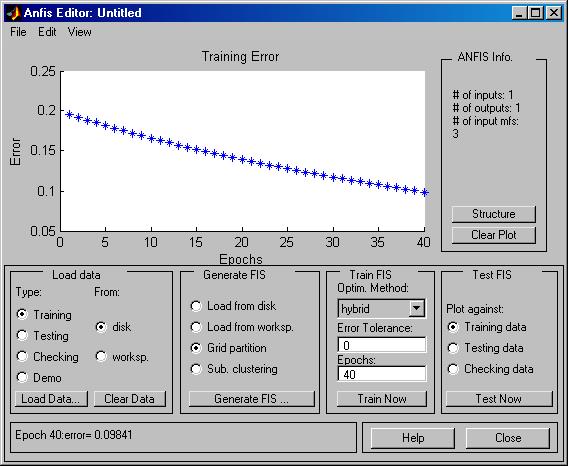
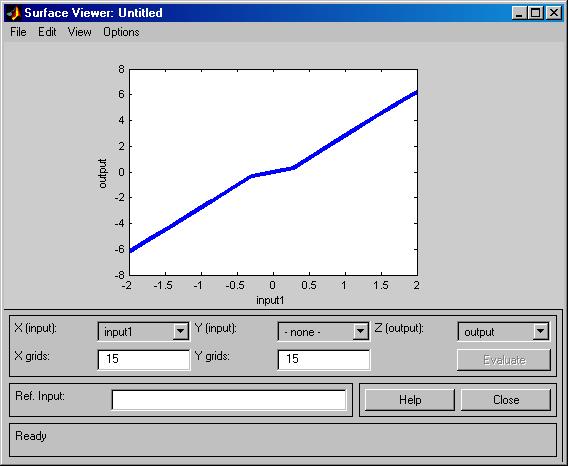
5.Выполнить анализ точности построенной нечеткой модели гибридной сети можно с помощью просмотра поверхности соответствующей системы нечеткого вывода
Визуальное сравнение изображенного графика с точным графиком функции у=x3 позволяет судить о достаточно высокой степени их совпадения, что может свидетельствовать об адекватности построенной нечеткой модели гибридной сети.
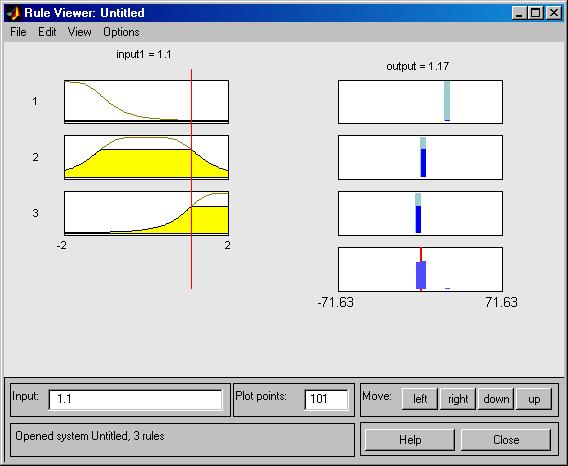
Анализ адекватности построенной модели можно выполнить с помощью просмотра правил соответствующей системы нечеткого вывода
Проверка построенной модели гибридной сети может быть выполнена для нескольких значений выходной переменной. С этой целью необходимо ввести конкретное значение в поле ввода Input (например, значение 1.1), после нажатия клавиши < Enter> с помощью построенной модели будет получено соответствующее значение выходной переменной (в данном случае значение 1.17). Сравнивая полученное значение с точным значением функции 1.331, получим относительную ошибку порядка 8%.
Менее удачной оказывается проверка для значения входной переменной 0.1, для которого построенная модель предлагает отрицательное значение -0.148. Очевидно, данный факт свидетельствует не в пользу адекватности построенной нечеткой модели и требует ее дополнительной настройки.
В общем случае дополнительная настройка модели может быть выполнена несколькими возможными способами. Наиболее приемлемыми из них представляются следующие:
1. Подготовка и загрузка большего по объему выборки файла с обучающими исходными данными.
2. Подготовка и загрузка дополнительного файла с проверочными исходными данными, сформированными для пар значений рассматриваемой математической функции, отсутствующих в выборке обучающих данных.
3. Редактирование типов и значений параметров функций принадлежности термов входной и выходной переменных с помощью редактора функций принадлежности системы MATLAB.
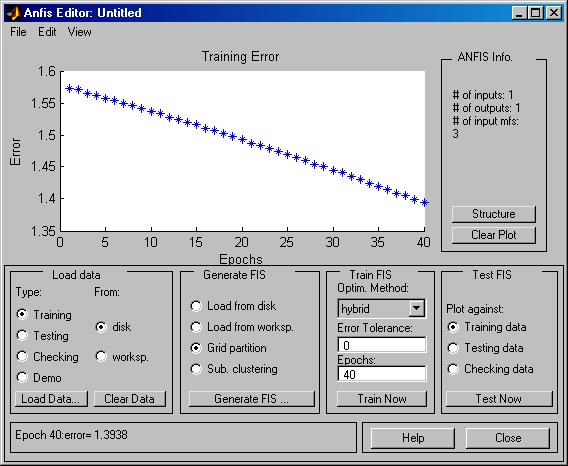
Более эффективным способом настройки, а точнее— модификации, данной нечеткой модели оказывается первый. С этой целью увеличим объем обучающей
выборки
После удаления всех ранее загруженных данных кнопкой Clear Data загрузим новую обучающую выборку. При генерации структуры новой FIS увеличим количество термов и, соответственно, количество функций принадлежности входной переменной до 5, оставив их тип без изменения (gbellmf). Процесс обучения выполним аналогично ранее рассмотренному. В результате будет получена новая система нечеткого вывода FIS, анализ которой показывает, что по сравнению с первым вариантом нечеткой модели она более точно описывает исходную математическую функцию.
Следует отметить, что даже простейшие рассмотренные примеры отражают творческий характер процесса построения и анализа моделей гибридных сетей. При этом выбор того или иного способа дополнительной настройки нечетких моделей зависит не только от специфики решаемой задачи, но и от объема доступной выборки обучающих и проверочных данных.