
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анализ полученных данных
|
|
6.1. ОБЩИЕ СВЕДЕНИЯ
Анализ полученных данных представляет важнейшую часть любого исследования, в связи с чем его выполнение осуществляется, как правило, наиболее опытным специалистом (обычно это сам руководитель темы). При этом выявление новых фактов и закономерностей является в значительной мере творческим процессом, который не может быть полностью формализован. Для того чтобы заметить проявление какого-либо нового эффекта, отличить его от ошибки эксперимента, исследователь должен обладать достаточно высоким профессионализмом и нередко способностью мыслить нестандартными категориями. Тем не менее, многолетняя практика проведения исследований показывает, что, несмотря на все многообразие используемых подходов, можно выделить довольно много общих правил и практических приемов, применимых к любым исследованиям. Такие правила если и не решают полностью поставленных задач, то по крайней мере существенно упрощают такие решения. Это особенно проявляется в исследованиях, относящихся к одному и тому же виду наук (технических, экономических, биологических и т. д.). Далее приводятся наиболее типичные приемы обработки экспериментальных данных, характерные для исследований количественного характера, т. е. связанных с использованием математических моделей, результатов измерений, наблюдений и т. д.
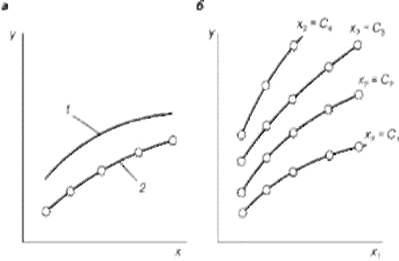
Рис. 6.1 Типичные способы изображения теоретических и экспериментальных зависимостей на начальном этапе анализа: а — при отображении зависимости от одной переменной, т. е. у — f(x): 1 — теоретическая кривая, 2 — экспериментальная кривая; б — при отображении зависимости от двух переменных типа у — f (x1, x2).
Первым этапом анализа полученных данных, как правило, является их систематизация путем представления таких данных в форме таблиц, карточек, каталогов и особенно их графическая интерпретация в виде графиков, схем, картограмм и т. д. Производится предварительная визуальная оценка построенных графиков, выдвигаются соответствующие гипотезы, намечаются дальнейшие этапы анализа. Обычно на этом этапе исследователь строит двумерные графики типа показанных на рис. 6.1, в том числе и при рассмотрении зависимости от двух переменных, ибо оксанометрические изображения сложны и неудобны для предварительного анализа. Зависимость от двух переменных у = f(x1, х2) обычно представляется графиком, в котором влияние одной из переменных отображается серией кривых, соответствующих различным фиксированным значениям этой переменной. На рис. 6.1б это значения х2 = C1, х2 = С2, х2 = С3, х2 = С4.
Для удобства анализа желательно соблюдать старое правило изображения получаемых данных: теоретические результаты представляются линией без выделения на ней отдельных точек, являющихся результатами расчета (линия 1 на рис. 6.1а), экспериментальные же результаты отображаются системой точек (или других простейших фигур), через которые проводится обобщающая линия — аппроксимирующая кривая (там же линия 2). Представление линий путем соединения точек между собой, как это сделано на рис. 6.1, допустимо лишь при малом разбросе или при очень малом числе точек. В большинстве же случаев аппроксимирующую линию следует проводить не через конкретные точки, а через их «центры тяжести» в каждом интервале изменения независимого переменного (подробнее об этом говорится в разделе о регрессионном анализе).
Как уже отмечалось, при анализе результатов экспериментов необходима особая осторожность и беспристрастность в оценках получаемых данных. Подтверждают или опровергают полученный результат эксперимента взгляды самого экспериментатора, внимание к такому результату должно быть одинаковым, особенно при малом числе таких данных.
Основная проблема первых этапов анализа экспериментальных данных в том, что отличить закономерность от случайности во многих случаях очень трудно. Для того чтобы свести к минимуму ошибки подобного типа, т. е. правильно интерпретировать экспериментальные данные и не перепутать случайность с закономерностью, используются методы математической статистики.