
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические сведения. Электронная цифровая подпись (ЭЦП) является аналогом обычной подписи и выполняет роль подтверждения подлинности документа.
|
|
Электронная цифровая подпись (ЭЦП) является аналогом обычной подписи и выполняет роль подтверждения подлинности документа.
Абоненты пересылают друг другу подписанные электронные документы. Для каждого абонента генерируется пара ключей: секретный и открытый. Секретный ключ хранится в тайне и используется для формирования электронной подписи. Открытый ключ предназначен для проверки ЭЦП и известен другим пользователям.
Для формирования ЭЦП применяются алгоритмы с открытым ключом.
Рассмотрим алгоритм цифровой подписи, основанный на RSA.
Сначала необходимо вычислить пару ключей (секретный ключ и открытый ключ). Для этого отправитель (автор) электронных документов вычисляет два больших простых числа Р и Q, затем находит их произведение N=Р*Q и значение функции j (N) = (Р -1)(Q -1).
Далее отправитель вычисляет число Е из условий:
Е 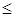 j (N), НОД (Е, j (N)) =1
j (N), НОД (Е, j (N)) =1
и число D из условий:
D < N, Е * D º 1 (mod j (N))
Пара чисел (Е, N) является открытым ключом. Эту пару чисел автор передает партнерам по переписке для проверки его цифровых подписей. Число D сохраняется автором как секретный ключ для подписывания.
Обобщенная схема формирования и проверки цифровой подписи RSA показана на рисунке 7.1.1.
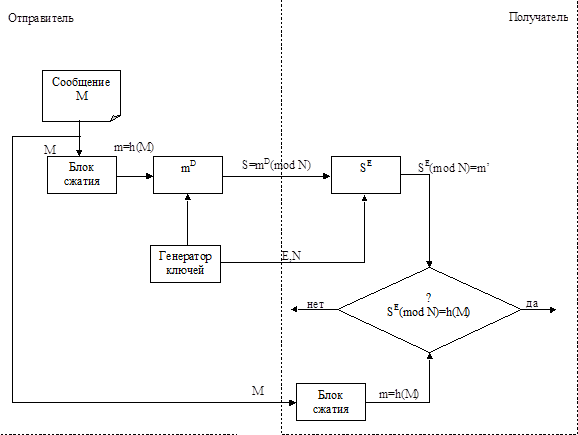
Рисунок 7.1.1 — Схема формирования и проверки цифровой подписи RSA
Допустим, что отправитель хочет подписать сообщение М перед его отправкой. Сначала сообщение М (блок информации, файл, таблица) сжимают с помощью хэш-функции h в целое число m:
m = h(M)
Затем вычисляют цифровую подпись S под электронным документом М, используя хэш-значение m и секретный ключ D:
S = mD(mod N)
Пара (М, S) передается партнеру-получателю как, электронный документ М, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа D.
После приема пары (M, S) получатель вычисляет хэш-значение сообщения М двумя разными способами. Прежде всего он восстанавливает хэш-значение m', применяя криптографическое преобразование подписи S с использованием открытого ключа Е:
m = SE(mod N)
Кроме того, он находит результат хэширования принятого сообщения М с помощью такой же хэш-функции h:
m = h(M)
Если соблюдается равенство вычисленных значений, т.е. SE (mod N) = h(M), то получатель признает пару (M, S) подлинной. Доказано, что только обладатель секретного ключа D может сформировать цифровую подпись S по документу М, а определить секретное число D по открытому числу Е не легче, чем разложить модуль N на множители.
Кроме того, можно строго математически доказать, что результат проверки цифровой подписи S будет положительным только в том случае, если при вычислении S был использован секретный ключ О, соответствующий открытому ключу Е. Поэтому открытый ключ Е иногда называют " идентификатором" подписавшего.