Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
По дисциплине: теория массового обслуживания
|
|
Межрегиональный центр переподготовки специалистов
ЗАЧЕТ
По дисциплине: теория массового обслуживания
Выполнила: Свистуненко И.Г.
Группа: ПБТ-49
Проверила: Разинкина Т.Э.
Новосибирск, 2015
Задание 9
В цехе работают три станка, которые ломаются с интенсивностями l1, l2, l3 (в сутки) соответственно. В штате состоят два наладчика, устраняющие поломки станков с интенсивностями m1, m2 (в сутки) соответственно. Требуется построить граф этой системы массового обслуживания и найти долю времени, когда оба наладчика заняты работой.
| l1 | l2 | l3 | m1 | m2 |
| 0.2 | 0.1 | 0.4 | 0.3 | 0.1 |
Решение
Принимаем, что заявки на ремонт станков не могут прийти одновременно, а наладчики не могут одновременно закончить работу (всегда кто-то заканчивает наладку раньше другого).
Также считаем, что наладчики не могут помогать друг другу в ремонте одного и того же станка. А один наладчик не может заниматься несколькими станками одновременно или по очереди.
Для решения задачи сделанных допущений недостаточно, так как по условию задачи неясно, какой из наладчиков приступает к работе, если пришла заявка на ремонт, а они оба свободны. То есть нужно установить приоритеты у наладчиков.
Также неясно, можно ли усреднять интенсивности входного или выходного потока.
Поэтому эти допущения делаем сами. Соответственно, получается несколько вариантов решений задачи.
а) Усредняем входные и выходные потоки (как это делали в контрольной работе)
Так же считаем, что если пришла заявка на ремонт, а оба наладчика свободны, то заказ принимает любой из наладчиков, случайно выбранный.
Находим среднюю интенсивность входного потока заявок на ремонт:
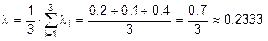(заявок в сутки).
Находим среднюю интенсивность устранения поломок (интенсивность освобождения наладчика):
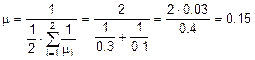(в сутки).
Введём следующие состояния системы: 0 – оба наладчика свободны, 1 – один наладчик занят (другой при этом свободен), 2 – заняты оба наладчика.
Граф такой системы изображён ниже:
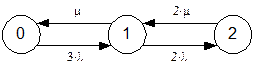
Найдём вероятность нахождения системы в состоянии 2 (оба наладчика заняты):
;
;
.
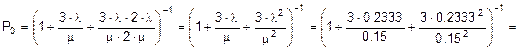
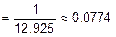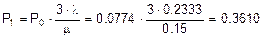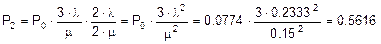Таким образом, доля времени, когда оба наладчика заняты работой, равна 0.5616.
б) Усредняем только входной поток заявок на ремонт.
Так же считаем, что если пришла заявка на ремонт, а оба наладчика свободны, то заказ принимает наладчик, устраняющий поломки станков с интенсивностью m1 (в сутки). Второй наладчик принимает заявку только тогда, когда первый занят.
Находим среднюю интенсивность входного потока заявок на ремонт:
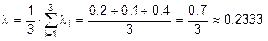(заявок в сутки).
Введём следующие состояния системы: 0 – оба наладчика свободны, a – занят первый наладчик (второй при этом свободен), b – занят второй наладчик (первый при этом свободен), 2 – заняты оба наладчика.
Граф такой системы изображён ниже:
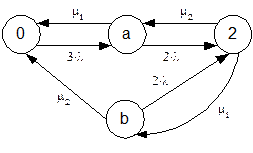
Составляем систему уравнений для стационарного режима (4 уравнения по числу состояний):
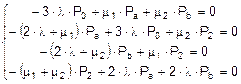
Подставляем в эту систему известные величины:
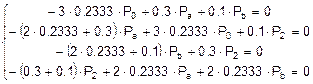Þ 
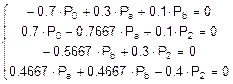
Проверяем правильность составленной системы (её определитель должен быть равен нулю) (определитель считаем в Excel):
.
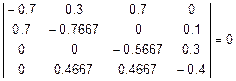Таким образом, система составлена правильно.
Заменяем в системе уравнений одно из уравнений (например, последнее) на нормировочное условие (сумма вероятностей всех состояний системы равна 1) и решаем его (решение выполнено в Excel):
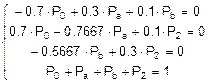Þ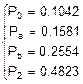 
Таким образом, доля времени, когда оба наладчика заняты работой, в этом случае равна 0.4823.
в) Ни входной, ни выходной потоки не усредняем.
Как и в предыдущем пункте считаем, что если пришла заявка на ремонт, а оба наладчика свободны, то заказ принимает наладчик, устраняющий поломки станков с интенсивностью m1 (в сутки). Второй наладчик принимает заявку только тогда, когда первый занят.
Введём следующие состояния системы:
0 – оба наладчика свободны;
a00, 0a0, 00a – занят первый наладчик (второй при этом свободен), причём он занят ремонтом 1-ого, 2-ого или третьего станка, соответственно;
b00, 0b0, 00b – занят второй наладчик (первый при этом свободен), причём он занят ремонтом 1-ого, 2-ого или третьего станка, соответственно;
ab0, a0b, 0ab, ba0, b0a, 0ba – заняты оба наладчика, причём каждый наладчик занят ремонтом того стоянка, номер которого совпадает с номером позиции наладчика в обозначении статуса: например: статус ab0 означает, что 1-ый наладчик занят первым станком, а 2-ой наладчик вторым.
Граф такой системы изображён ниже:
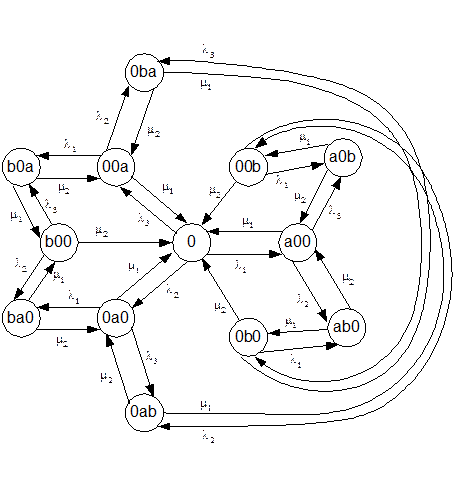
Составляем систему уравнений для стационарного режима (13 уравнений по числу состояний):
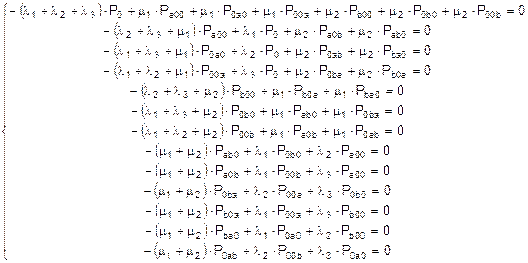
Подставляем в эту систему известные величины и заменяем в ней одно из уравнений (например, последнее) на нормировочное условие (сумма вероятностей всех состояний системы равна 1) и решаем его (решение выполнено в Excel):
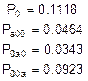
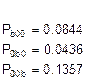
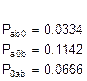
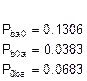
Сумма последних шести вероятностей и есть доля времени, когда оба наладчика заняты работой: 0.4514.
|