
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание лабораторного занятия
|
|
Алматинская академия экономики и статистики
Кафедра «__ Информатика_»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ
ЛАБОРАТОРНЫХ ЗАНЯТИЙ
по дисциплине «__________ Эконометрика _________»
специальности « 5В050600 Экономика, 5В050700 Менеджмент, 5В050800 Учет и аудит, 5В050900 Финансы и 5В051100 Маркетинг »
(«шифр-название»)
Алматы, 2014 г.
Методические укзания к выполнению лабораторных работ №7.
Парная регрессия и корреляция в экономических исследованиях
В эконометрике широко используются методы статистики. Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика прежде всего связана с методами регрессии и корреляции.
В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
Задание лабораторного занятия
Пример 1.1. Для определения зависимости между сменной добычей угля на одного рабочего (переменная Y, измеряемая в тоннах) и мощностью угольного пласта (переменная X, измеряемая в метрах) на 10 шахтах были проведены исследования, результаты которых представлены таблицей 1.1.
Таблица 1.1
| i | ||||||||||
| xi | ||||||||||
| yi |
Требуется определить:
1. Вычисление коэффициентов уравнения линейной регрессии;
2. Вычисление выборочного коэффициента корреляции;
3. Вычисление оценок дисперсий коэффициентов парной линейной регрессии;
4. Построение интервальной оценки для функции парной линейной регрессии;
5. Проверка значимости уравнения линейной регрессии по критерию Фишера.
3. Методические рекомендации по выполнению лабораторных заданий
Простая (парная) регрессия представляет собой регрессию между двумя переменными – у и х, т.е. модель вида:
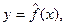
где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак - фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида:
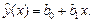 (1.1)
(1.1)
Пространственная выборка для построения этого уравнения взята из следующего примера.
Расчетные соотношения. Коэффициенты, определяемые на основе метода наименьших квадратов, являются решением системы уравнений
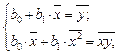 (1.2)
(1.2)
где
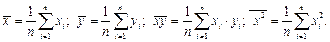 (1.3)
(1.3)
Решая эту систему уравнений, получаем
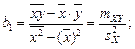 (1.4)
(1.4)
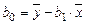 , (1.5)
, (1.5)
где mXY – выборочное значение корреляционного момента, определенного по формуле:
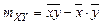 , (1.6)
, (1.6)
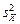 – выборочное значение дисперсии величины X, определяемой по формуле:
– выборочное значение дисперсии величины X, определяемой по формуле:
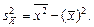 (1.7)
(1.7)
Решение. Вычислим эти коэффициенты 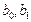 , используя табличный процессор Excel (версия XP). На рис. 1.1 показан фрагмент документа Excel, в котором: а) размещены данные таблицы 1; б) запрограммировано вычисление коэффициентов
, используя табличный процессор Excel (версия XP). На рис. 1.1 показан фрагмент документа Excel, в котором: а) размещены данные таблицы 1; б) запрограммировано вычисление коэффициентов 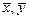 ,
, 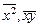 системы (1.2); в) запрограммировано вычисление b 0, b 1 по формулам (1.4), (1.5) соответственно. Заметим, что для вычисления средних значений используется функция Excel СРЗНАЧ(диапазон ячеек). В результате выполнения запрограммированных вычислений получаем b 0 = –2.75; b 1 = 1.016, а само уравнение регрессии (1.1) примет вид
системы (1.2); в) запрограммировано вычисление b 0, b 1 по формулам (1.4), (1.5) соответственно. Заметим, что для вычисления средних значений используется функция Excel СРЗНАЧ(диапазон ячеек). В результате выполнения запрограммированных вычислений получаем b 0 = –2.75; b 1 = 1.016, а само уравнение регрессии (1.1) примет вид
 . (1.8)
. (1.8)
Задание. Используя уравнение (1.8), определите производительность труда шахтера, если толщина угольного слоя равна: а) 8.5 метров (интерполяция данных); б) 14 метров (экстраполяция данных).
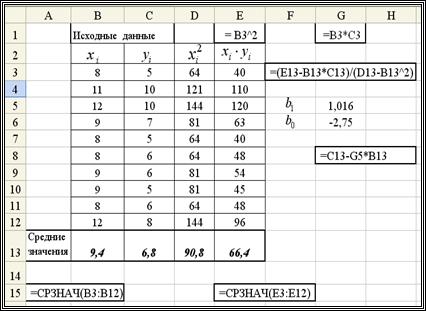
Рис. 1.1. Вычисление коэффициентов линейной регрессии
 Расчетные соотношения. Выборочный коэффициент корреляции определяется соотношением
Расчетные соотношения. Выборочный коэффициент корреляции определяется соотношением
 (1.9)
(1.9)
где 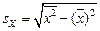 ,
, 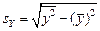 ,
, 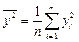 . (1.10)
. (1.10)
Решение. Фрагмент документа Excel, вычисляющего величины: коэффициента корреляции (формула (1.9)); 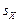 ,
, 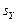 (формулы (1.10), приведен на рис. 1.2.
(формулы (1.10), приведен на рис. 1.2.
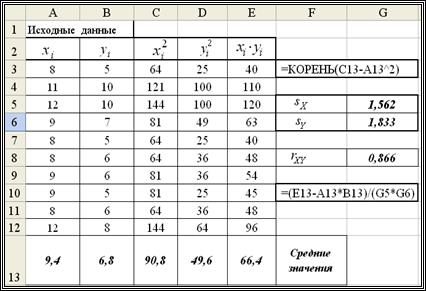
Рис. 1.2. Вычисление коэффициента корреляции
Цель работы. Вычислить оценки 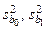 для дисперсий коэффициентов b 0, b 1, определенных в лабораторной работе № 1.1.
для дисперсий коэффициентов b 0, b 1, определенных в лабораторной работе № 1.1.
Расчетные соотношения. Оценки для дисперсий коэффициентов 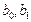 определяются формулами:
определяются формулами:
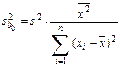 ,
, 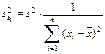 (1.11)
(1.11)
где 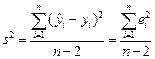 - оценка дисперсии
- оценка дисперсии 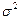 .
.
Решение. На рис. 1.3 показан фрагмент документа Excel, в котором выполнены вычисления оценок дисперсий 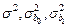 .
.
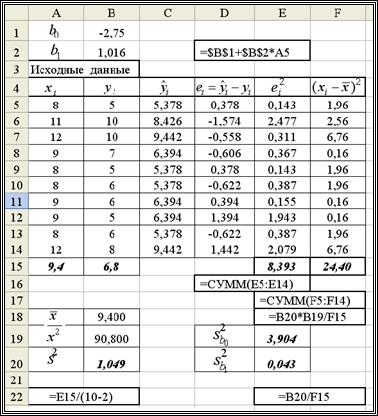
Рис. 1.3. Вычисление оценок для дисперсий коэффициентов
Заметим, что
· значения коэффициентов 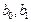 взяты из лабораторной работы № 1.1 и ячейки (В1, В2), в которых они находятся, имеют абсолютную адресацию ($В$1, $В$2) в выражениях, вычисляющих значения регрессии
взяты из лабораторной работы № 1.1 и ячейки (В1, В2), в которых они находятся, имеют абсолютную адресацию ($В$1, $В$2) в выражениях, вычисляющих значения регрессии 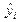 ;
;
· значение 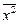 (ячейка В19) взято из лабораторной работы № 1.1.
(ячейка В19) взято из лабораторной работы № 1.1.
Получаем следующие значения: 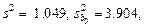
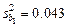 .
.
Функции Excel для вычисления коэффициентов парной линейной регрессии
Функция ОТРЕЗОК. Вычисляет коэффициент 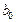 и обращение имеет вид
и обращение имеет вид
ОТРЕЗОК(диапазон_значений_ 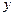 ; диапазон_значений_
; диапазон_значений_ 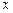 ).
).
Функция НАКЛОН. Вычисляет коэффициент 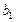 и обращение имеет вид
и обращение имеет вид
НАКЛОН(диапазон_значений_ 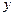 ; диапазон_значений_
; диапазон_значений_ 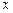 ).
).
Функция ПРЕДСКАЗ. Вычисляет значение линейной парной регрессии при заданном значении независимой переменной (обозначена через 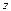 ) и обращение имеет вид
) и обращение имеет вид
ПРЕДСКАЗ(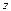 ; диапазон_значений_
; диапазон_значений_ 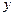 ; диапазон_значений_
; диапазон_значений_ 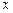 ).
).
Функция СТОШYX. Вычисляет оценку 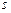 для среднеквадратического отклонения
для среднеквадратического отклонения 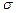 возмущений
возмущений 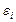 и обращение имеет вид (YX – латинские буквы):
и обращение имеет вид (YX – латинские буквы):
СТОШYX(диапазон_значений_ 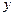 ; диапазон_значений_
; диапазон_значений_ 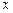 ).
).
Решение. Фрагмент документа Excel, вычисляющего требуемые величины приведен на рис. 1.4.  Обратите внимание на использовании абсолютной адресации при вычислении
Обратите внимание на использовании абсолютной адресации при вычислении 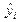 .
.
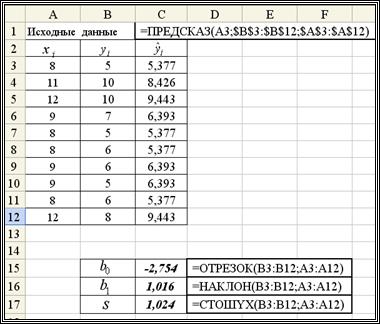
Рис. 1.4. Использование функций Excel
Цель работы. Построение интервальной оценки для функции регрессии 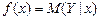 с надежностью g = 0.95, используя для этого уравнение регрессии
с надежностью g = 0.95, используя для этого уравнение регрессии 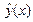 , построенное в лабораторной работе № 1.1.
, построенное в лабораторной работе № 1.1.
Расчетные соотношения. Интервальная оценка (доверительный интервал) для 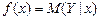 (при заданном значении
(при заданном значении 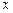 ) с надежностью (доверительной вероятностью) равной g определяется выражением
) с надежностью (доверительной вероятностью) равной g определяется выражением
 . (1.12)
. (1.12)
Оценка 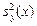 для дисперсии функции
для дисперсии функции 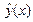 имеет вид
имеет вид
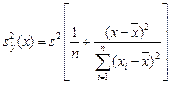 , (1.13)
, (1.13)
где 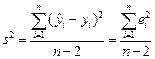 - оценка дисперсии
- оценка дисперсии 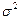 . Таким образом, в (1.12) входят две величины
. Таким образом, в (1.12) входят две величины 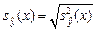 (зависит от
(зависит от 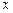 ) и
) и 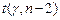 , вычисляемая с помощью функции Excel:
, вычисляемая с помощью функции Excel:
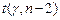 =СТЬЮДРАСПОБР(
=СТЬЮДРАСПОБР(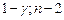 ).
).
Решение. Значения нижней 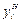 и верхней
и верхней 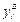 границ интервала (1.12) будем вычислять для
границ интервала (1.12) будем вычислять для 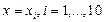 . Фрагмент документа, осуществляющий эти вычисления, приведен на рис. 1.5.
. Фрагмент документа, осуществляющий эти вычисления, приведен на рис. 1.5.
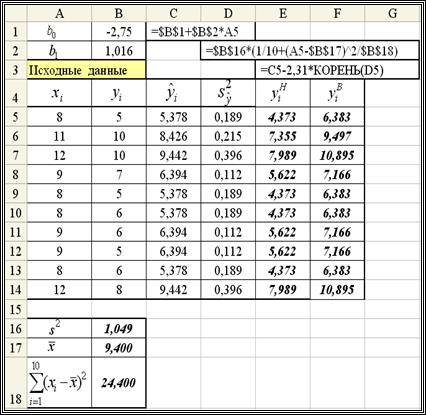
Рис.1.5. Построение интервальной оценки для 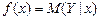
Величины 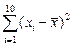 ,
, 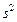 ,
, 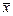 (ячейки В16: В18) и коэффициенты
(ячейки В16: В18) и коэффициенты 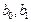 (В1: В2) взяты из предыдущих лабораторных работ. Величина
(В1: В2) взяты из предыдущих лабораторных работ. Величина
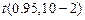 = СТЬЮДРАСПОБР(
= СТЬЮДРАСПОБР(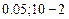 ) = 2.31.
) = 2.31.
Расчетные соотношения. Уравнение парной регрессии значимо с уровнем значимости a, если выполняется следующее неравенство:
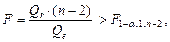 (1.14)
(1.14)
где F g; 1; n -2 – значения квантиля уровня g F -распределения с числами степеней свободы k 1 = 1 и k 2 = n – 2. Для вычисления квантиля можно использовать следующее выражение
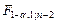 = FРАСПОБР(
= FРАСПОБР(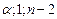 ). (1.15)
). (1.15)
Суммы 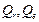 , входящие в (1.14) определяются выражениями:
, входящие в (1.14) определяются выражениями:
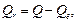
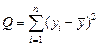 ,
, 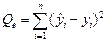 . (1.16)
. (1.16)
Критерий (1.14) часто называют критерием Фишера или F-критерием.
Решение. На рис. 1.6 приведен фрагмент документа Excel, вычисляющего значения Qe, 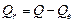 и критерий F. В столбце D значения вычисляются по формуле
и критерий F. В столбце D значения вычисляются по формуле 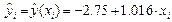 . Значения коэффициентов
. Значения коэффициентов 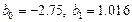 взяты из лабораторной работы № 1.1.
взяты из лабораторной работы № 1.1.
Получены следующие значения 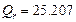 ,
, 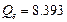 ,
, 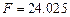 . По формуле (1.15) вычисляем квантиль F 0.95; 1; 8 = 5.32. Неравенство (1.14) выполняется, т. е. 24.04 > 5.32 и поэтому уравнение регрессии
. По формуле (1.15) вычисляем квантиль F 0.95; 1; 8 = 5.32. Неравенство (1.14) выполняется, т. е. 24.04 > 5.32 и поэтому уравнение регрессии 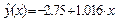 значимо с уровнем значимости a = 0.05.
значимо с уровнем значимости a = 0.05.

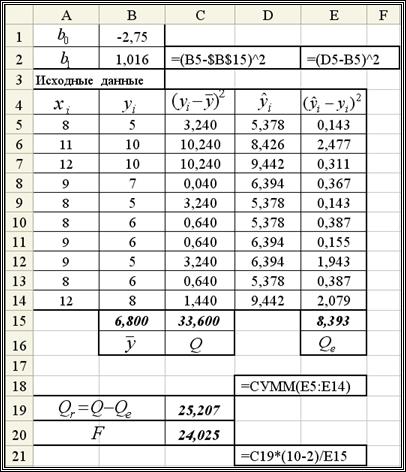
Рис. 1.6. Вычисление величины F – критерия