Предпочтения потребителя и их оценка. Кривые безразличия.

В экономической теории существует два подхода к оценке полезности. Первый (кардиналистский) считает, что потребитель может количественно определить величину полезности, приносимую благом. Поэтому общая полезность принимает вид функции полезности от объема благ U=f(X), где X=(X₁, X₂, …X_n) набор товаров 1, 2, …n

Второй подход (ординалистский) считает, что не представляется возможным количественно измерить полезность, поэтому предлагает оценивать полезность на основании предпочтения потребителем одного набора благ по сравнению с другим, т.е. U(X₁) > U(X₂)

Предпочтительнее те наборы благ, которые имеют более высокий уровень полезности для потребителя с его субъективной точки зрения.

Ординалистский подход опирается на понятие кривых безразличия. Для того, чтобы понять как они строятся, предположим существование всего двух товаров. Пусть потребитель выбирает первый из них в количестве q₁, а второй – в количестве q₂. Тогда набор (q₁; q₂) определит потребительскую корзину, включающую то или иное количество первого и второго товаров и обладающую некоторым качеством, которое можно измерить. (Если наборы пищевые, то таким качеством будет калорийность набора или содержание витамина С; для обуви – срок носки и т.д.).

Каждой потребительской корзине соответствует некоторое число U, называемое полезностью. Таблично при функции полезности, имеющей вид U=q₁× q₂, это можно изобразить так:

q1 q2

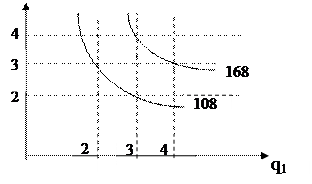Рис. 3

Совокупность потребительских корзин, обеспечивающих потребителю одинаковый уровень удовлетворения, то есть имеющих одинаковую для него полезность, называется кривой безразличия.

Свойства стандартных кривых безразличия следующие. Во-первых, кривая безразличия не может иметь участки возрастания. Во-вторых, кривые безразличия с разным уровнем полезности никогда не пересекаются. В-третьих, кривая безразличия может быть проведена через каждую точку в пространстве товара. И, наконец, кривая безразличия выпукла к началу координат и предельная норма замещения (наклон кривой безразличия) уменьшается при движении по кривой безразличия сверху вниз.

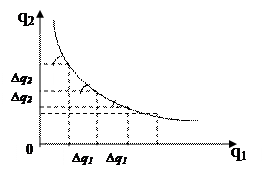
Предельная норма замещения (MRS) - количество товара q₂, от которого потребитель должен отказаться, чтобы получить еще одну единицу товара q₁, оставаясь при этом на той же кривой безразличия. Она равна

MRS = - ∆ q₂ /∆ q₁.

Пусть функция полезности имеет вид: U=q₁× q₂. Будем рассматривать уровень полезности U= 60. Пусть q₁ = 1; q₂ = 60.

M RS 30 10 5 3 2

При увеличении q₁ на единицу мы можем уменьшить q₂ на 30 единиц и при этом остаться на том же уровне полезности. (Но с каждой единицей q₁ нам все труднее отказаться от q₂).

Геометрически предельная норма замещения равна тангенсу угла наклона отрезка АВ к горизонтальной оси. При движении вдоль кривой норма замещения убывает, следовательно, убывает угол. А это означает, что кривая безразличия является выпуклой в сторону начала координат (рис. 3).

Рис. 3 Рис. 4