Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пояснение к работе
|
|
Лабораторная работа № 8
Расчет аналоговых фильтров с использованием пакеты программы «MATHCAD»
Цель работы
Изучение процесса расчета аналоговых фильтров в программной среде «MATHCAD».
Подготовка к работе
Изучить по литературе [1] содержание страниц 231-233, 397-398, а также в конспекте лекций по дисциплине ОКП и М РЭС раздел «оптимизация».
Литература
[1] – В.И.Каганов, Радиотехника плюс компьютер плюс «MATHCAD». М.2001г.
- конспект лекций по дисциплине ОКП и М РЭС.
Пояснение к работе
В данной лабораторной работе необходимо определить оптимальный тип аналогового фильтра нижних частот для заданных параметров.
Заданными параметрами являются
fPP – граничная частота полосы пропускания;
fPn – граничная частота полосы непропускания;
Аmax – неравномерность затухания в полосе пропускания;
Аmin – рабочее затухание на fPn.
Заданы также нормы на групповое время запаздывания для ряда частот в соответствии со стандартами для трактов радиовещательных сигналов (таблица 1). В таблице значения частоты нормированы относительно fPP. (ώ =f/ fPP).
Таблица 1
| ώ | 4·10-3 | 7, 5-10-3 | 0, 01 | 0, 64 | 0, 7 | 1, 4 | 1, 5 |
| τ d, мс |
Таким образом расчет предполагает выбор фильтра, обеспечивающего заданные требования с наименьшим порядком n и удовлетворяющего требованиям по групповому запаздыванию сигнала.
Поскольку групповое время запаздывания является производной от аргумента амплитудно-частотной характеристики фильтра
,
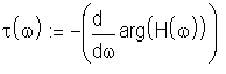а H(w) определяется через значения полюсов аппроксимирующих полиномов, количество и значения которых можно проводить по следующей схеме:
- определение порядков фильтров Баттерворта и Чебышева для заданных значений Аmax,
Аmin, wn (нормированной частоты полосы пропускания fpn, деленной на fpp),
для фильтра Баттерворта:
,
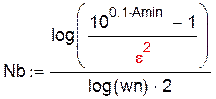где
,
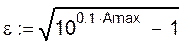а для фильтра Чебышева
- для фильтра, имеющего наименьший порядок рассчитывается зависимость τ (ώ) и строятся две зависимости на одном графике,
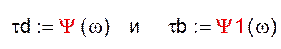- для фильтра Баттерворта, а для фильтра Чебышева:
.
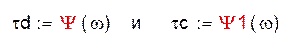(для фильтра Чебышева), где ώ нормированная относительно fpp частота (f, деленная на fpp)
τ d строится по данным таблицы 1 путем кусочно-линейной или сплайн интерполяции.
- если для всех частот, приведенных в таблице 1
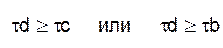
то фильтр удовлетворяет всем требованиям поставленной задачи. В противном случае необходимо произвести проверку по τ (ώ) для другого типа фильтра (у которого порядок выше). Если и у него не удовлетворяются требования по групповой задержке, то можно сделать вывод, что при заданных значениях Аmax, Аmin и ώ n данные фильтры не могут удовлетворять требованиям стандартов по групповому запаздыванию сигнала.