
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
З а д а ч а 10
|
|
Чтобы найти точку 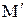 , симметричную точке
, симметричную точке 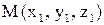 относительно прямой, нужно найти проекцию точки М на прямую
относительно прямой, нужно найти проекцию точки М на прямую 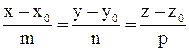 . Проекция будет серединой отрезка
. Проекция будет серединой отрезка 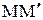 . Проекция есть точка пересечения прямой с перпендикулярной к ней плоскостью, проходящей через точку М. Так как вектор
. Проекция есть точка пересечения прямой с перпендикулярной к ней плоскостью, проходящей через точку М. Так как вектор 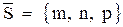 перпендикулярен этой плоскости, ее уравнение запишем в виде
перпендикулярен этой плоскости, ее уравнение запишем в виде
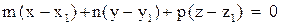 .
.
Далее, как и в предыдущей задаче, находим точку Р (точку пересечения данной прямой с найденной плоскостью). Зная середину отрезка 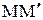 , найдем координаты точки
, найдем координаты точки 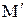 . Чтобы найти точку
. Чтобы найти точку 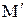 , симметричную точке
, симметричную точке  относительно плоскости
относительно плоскости 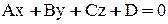 , нужно найти проекцию точки М на плоскость. Проекция будет серединой отрезка
, нужно найти проекцию точки М на плоскость. Проекция будет серединой отрезка 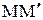 .
.
Проекция точки 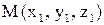 на плоскость будет точкой пересечения перпендикуляра к плоскости, проходящего через точку М, с самой плоскостью. Вектор
на плоскость будет точкой пересечения перпендикуляра к плоскости, проходящего через точку М, с самой плоскостью. Вектор 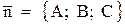 будет направляющим вектором перпендикулярной прямой.
будет направляющим вектором перпендикулярной прямой.
Далее, как и в задаче 9, находим точку пересечения перпендикуляра с данной плоскостью.
Зная середину отрезка 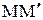 , найдем координаты точки
, найдем координаты точки 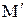 .
.