
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 3
|
|
| 1. | При каких размерах коробка (без крышки), изготовленная из квадратного листа картона, со стороной a, имеет наибольшую вместимость? |
| 2. | Среди всех прямоугольников, имеющих данный периметр 2 a, найти тот, площадь которого наибольшая. |
| 3. | Кусок проволоки данной длины 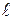 согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей. согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей.
|
| 4. | Число 50 записать в виде суммы двух чисел, сумма кубов которых наименьшая. |
| 5. | Записать число 625 в виде произведения двух положительных чисел так, чтобы сумма их квадратов была наименьшая. |
| 6. | Из всех прямоугольников, площадь которых равна 9 см2, найти прямоугольник с наименьшим периметром. |
| 7. | Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 600 см2, найти параллелепипед наибольшего объема. |
| 8. | Из всех прямоугольников с периметром Pнайти прямоугольник с наименьшей диагональю. |
| 9. | Из всех равнобедренных треугольников с периметром P найти треугольник с наибольшей площадью. |
| 10. | Из всех прямоугольных треугольников, у которых сумма одного катета и гипотенузы равна 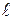 , найти треугольник с наибольшей площадью. , найти треугольник с наибольшей площадью.
|
| 11. | Найти размеры открытого сверху цилиндрического бака данного объема 64 л, при которых на его изготовление пойдет минимальное количество жести. |
| 12. | Окно магазина имеет форму прямоугольника, заканчивающегося полукругом. Периметр фигуры равен 15 м. При каком размере полукруга окно будет пропускать наибольшее количество света? |
| 13. | Образующая конического сосуда равна 25 см. Какой должна быть его высота, чтобы вместимость сосуда была наибольшей. |
| 14. | Определить наибольшую площадь прямоугольника, вписанного в круг радиусом r. |
| 15. | Решеткой длиной 120 м нужно огородить площадку наибольшей площади. Найти размеры этой площадки. |
| 16. | Разложить число 10 на два слагаемых так, чтобы произведение их было наибольшим. |
| 17. | При каких размерах коробка (без крышки), изготовленная из квадратного листа картона, со стороной a, имеет наибольшую вместимость? |
| 18. | Среди всех прямоугольников, имеющих данный периметр 2 a, найти тот, площадь которого наибольшая. |
| 19. | Кусок проволоки данной длины 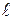 согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей. согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей.
|
| 20. | Число 50 записать в виде суммы двух чисел, сумма кубов которых наименьшая. |
| 21. | Записать число 625 в виде произведения двух положительных чисел так, чтобы сумма их квадратов была наименьшая. |
| 22. | Из всех прямоугольников, площадь которых равна 9 см2, найти прямоугольник с наименьшим периметром. |
| 23. | Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 600 см2, найти параллелепипед наибольшего объема. |
| 24. | Из всех прямоугольников с периметром Pнайти прямоугольник с наименьшей диагональю. |
| 25. | Из всех равнобедренных треугольников с периметром P найти треугольник с наибольшей площадью. |
| 26. | Из всех прямоугольных треугольников, у которых сумма одного катета и гипотенузы равна 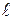 , найти треугольник с наибольшей площадью. , найти треугольник с наибольшей площадью.
|
| 27. | Найти размеры открытого сверху цилиндрического бака данного объема 64 л, при которых на его изготовление пойдет минимальное количество жести. |
| 28. | Окно магазина имеет форму прямоугольника, заканчивающегося полукругом. Периметр фигуры равен 15 м. При каком размере полукруга окно будет пропускать наибольшее количество света? |
| 29. | Образующая конического сосуда равна 25 см. Какой должна быть его высота, чтобы вместимость сосуда была наибольшей. |
| 30. | Определить наибольшую площадь прямоугольника, вписанного в круг радиусом r. |
ЗАДАНИЕ 4. Найти точки перегиба функции:
1. 
| 2. 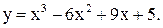
| 3. 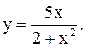
|
4. 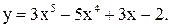
| 5. 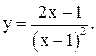
| 6. 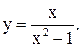
|
7. 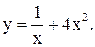
| 8. 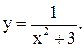
| 9. 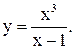
|
10. 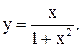
| 11. 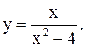
| 12. 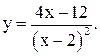
|
13. 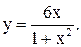
| 14. 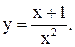
| 15. 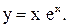
|
16. 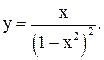
| ||
17. 
| 18. 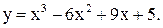
| 19. 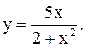
|
20. 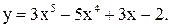
| 21. 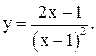
| 22. 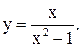
|
23. 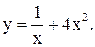
| 24. 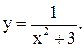
| 25. 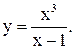
|
26. 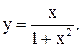
| 27. 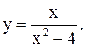
| 28. 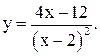
|
29. 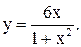
| 30. 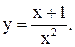
|
ЗАДАНИЕ 5. Найти асимптоты графика функции:
1. 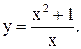
| 2. 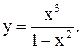
| 3. 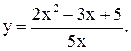
|
4. 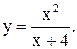
| 5. 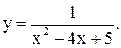
| 6. 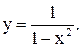
|
7. 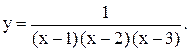
| 8. 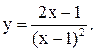
| 9. 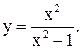
|
10. 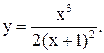
| 11. 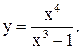
| 12. 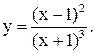
|
13. 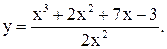
| 14. 
| 15. 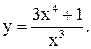
|
16. 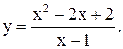
| ||
17. 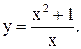
| 18. 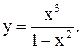
| 19. 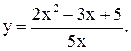
|
20. 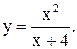
| 21. 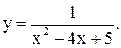
| 22. 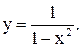
|
23. 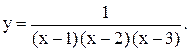
| 24. 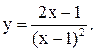
| 25. 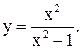
|
26. 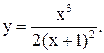
| 27. 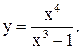
| 28. 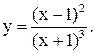
|
29. 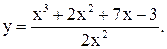
| 30. 
|
ЗАДАНИЕ 6. Исследовать функцию и построить ее график:
1. 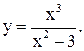
| 2. 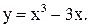
| 3. 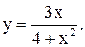
| 4. 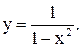
|
5. 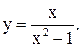
| 6. 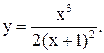
| 7. 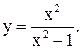
| 8. 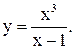
|
9. 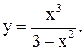
| 10. 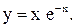
| 11. 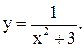
| 12. 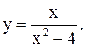
|
13. 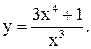
| 14. 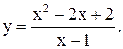
| 15. 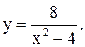
| 16. 
|
17. 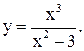
| 18. 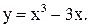
| 19. 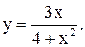
| 20. 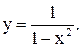
|
21. 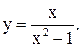
| 22. 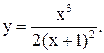
| 23. 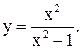
| 24. 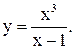
|
25. 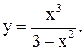
| 26. 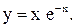
| 27. 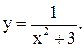
| 28. 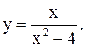
|
29. 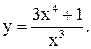
| 30. 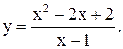
|
Образец выполнения контрольной работы
“Приложение ПРОИЗВОДНОЙ”
1) Исследовать на экстремум функцию 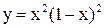 .
.
Решение. Найдем точки, подозрительные на экстремум. Для этого возьмем производную 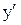 и приравняем ее нулю.
и приравняем ее нулю.
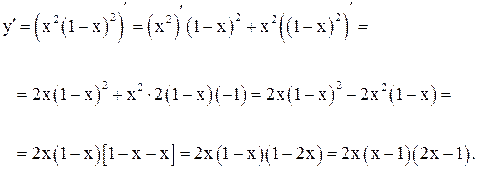
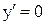 при
при 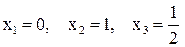 .
.
|













Рисунок 1
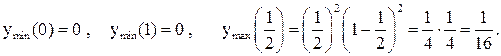
На тех интервалах, где 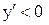 , функция убывает; где
, функция убывает; где 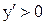 , функция возрастает. Поэтому интервалы возрастания функции
, функция возрастает. Поэтому интервалы возрастания функции 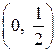 и
и 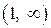 , интервалы убывания функции:
, интервалы убывания функции: 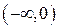 и
и 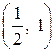 .
.
По рисунку 1 видно, что в точках 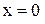 и
и 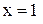 функция принимает свои минимальные значения, а при
функция принимает свои минимальные значения, а при 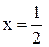 – максимальное. Найдем эти значения:
– максимальное. Найдем эти значения:
Ответ: 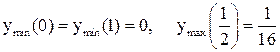 .
.
2) Найти наибольшее и наименьшее значения функции 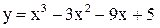 на отрезке
на отрезке 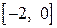 .
.
Решение. Так как свои наименьшее и наибольшее значения непрерывная на отрезке функция может принимать либо на концах этого отрезка, либо в точках экстремума, входящих в этот отрезок, то находим значения исследуемой функции во всех этих точках и среди них выбираем наибольшее и наименьшее значения:
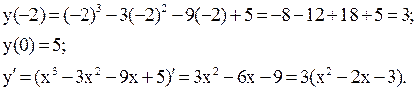
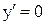 при
при 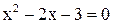 ,
,
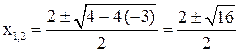 ,
,
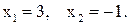
Найдем значение функции только при  . Так как
. Так как 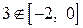 , то
, то
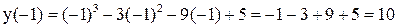 .
.
Выбираем наибольшее значение функции из найденных трех чисел – это 10. Теперь наименьшее – это 3.
Ответ: 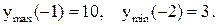
3) Найти точки перегиба функции 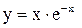 .
.
Решение. Так как точками перегиба являются те точки из области допустимых значений, где вторая производная 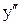 меняет знак, сначала найдем
меняет знак, сначала найдем 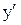 , затем
, затем 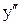 и приравняем
и приравняем 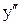 к нулю:
к нулю:
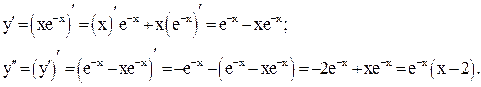
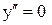 при
при 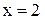 , т. к.
, т. к. 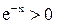 для всех
для всех 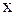 .
.
|
|





4) Найти асимптоты графика 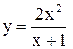 .
.
Так как вертикальную асимптоту имеет функция с разрывом 2-го рода в точке 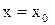 , сначала найдем точки разрыва и исследуем поведение функции в их окрестностях.
, сначала найдем точки разрыва и исследуем поведение функции в их окрестностях.
О.Д.З. 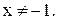
Значит, 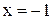 – точка разрыва, так как функция в этой точке не определена. Найдем предел слева и предел справа функции
– точка разрыва, так как функция в этой точке не определена. Найдем предел слева и предел справа функции 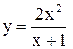 при подходе к точке
при подходе к точке 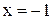 . Выясним, разрыв какого рода терпит данная функция в этой точке.
. Выясним, разрыв какого рода терпит данная функция в этой точке.
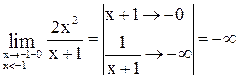 . Предел слева равен
. Предел слева равен 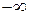 .
.
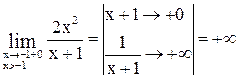 . Предел слева равен
. Предел слева равен 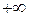 .
.
Так как односторонние пределы бесконечны, то в точке 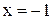 разрыв 2-го рода, поэтому уравнением вертикальной асимптоты будет
разрыв 2-го рода, поэтому уравнением вертикальной асимптоты будет 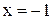 .
.
Функция также может иметь или не иметь наклонные асимптоты. Если они есть, то их уравнение запишем в виде 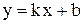 ,
,
где 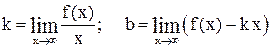 .
.
Найдем правую наклонную асимптоту при 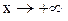 .
.
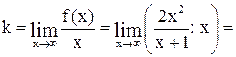

Применяем правило Лопиталя:
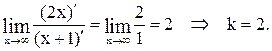
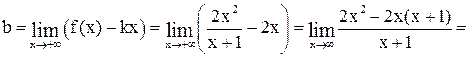
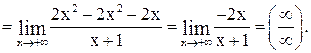
Применяем правило Лопиталя: 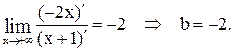
|
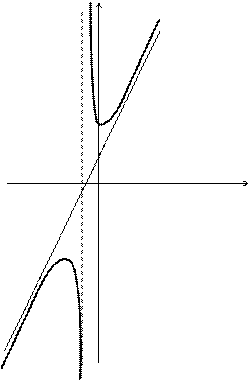 у
у
-2
-2 -1 1 х
-2 -
Рисунок 3
5) Исследовать функцию 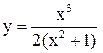 и построить ее график.
и построить ее график.
Исследование функции будем проводить по плану.
1. Найдем О.Д.З. и, если есть асимптоты О.Д.З., 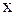 – любое. Следовательно, нет точек разрыва, поэтому вертикальных асимптот нет.
– любое. Следовательно, нет точек разрыва, поэтому вертикальных асимптот нет.
2. Найдем точки пересечения графика функции с осями координат, исследуем функцию на четность, тригонометрические функции – на периодичность. Пусть 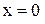 , тогда
, тогда 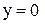 . Проверим четность функции:
. Проверим четность функции:
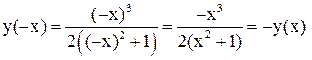 .
.
Значит, данная функция нечетная, и ее график симметричен относительно начала координат.
3. Исследуем монотонность функции с помощью 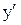 .
.
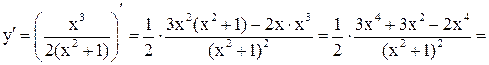
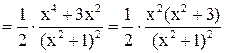 .
.
|
|

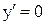 при
при 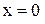
 |
+ +


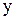 0 х
0 х
Рисунок 4
4. С помощью 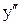 находим точки перегиба.
находим точки перегиба.
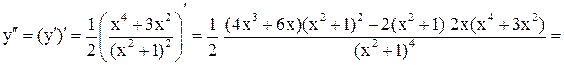
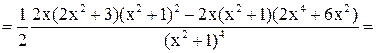

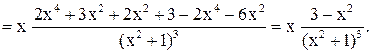
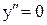 при
при 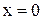 и
и 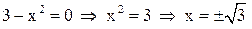 .
.
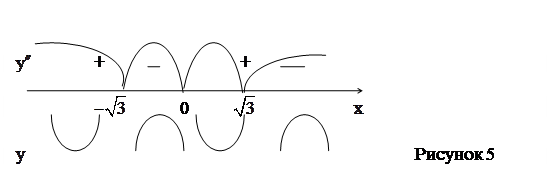 |
Все точки, в которых 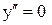 , являются точками перегиба, так как в них
, являются точками перегиба, так как в них 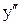 меняет знак на противоположный (рис. 5).
меняет знак на противоположный (рис. 5).
Найдем значения функции в этих точках:
 .
.
5. Найдем наклонные асимптоты, если они есть: 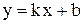 .
.
Сначала 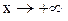 , тогда
, тогда 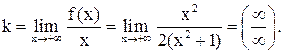
По правилу Лопиталя: 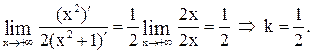
 Теперь найдем
Теперь найдем 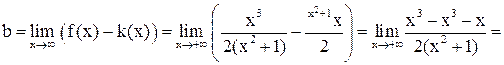
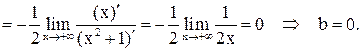
Получаем 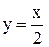 – уравнение правой асимптоты. Повторяя прежние рассуждения уже при
– уравнение правой асимптоты. Повторяя прежние рассуждения уже при 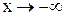 , получим уравнение левой асимптоты:
, получим уравнение левой асимптоты: 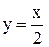 .
.
6. Строим график функции, начертив сначала все асимптоты, отметив точки экстремума, точки перегиба и точки пересечения с осями координат (рис. 6).
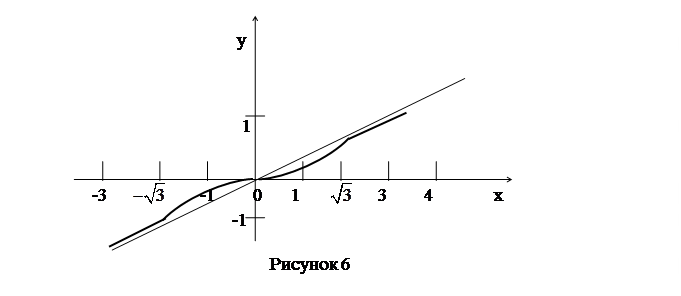
|
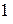
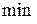
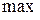
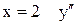 изменила знак, то функция
изменила знак, то функция 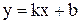 и получаем уравнение правой асимптоты
и получаем уравнение правой асимптоты 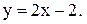 Найдем левую асимптоту при
Найдем левую асимптоту при 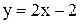 (рис. 3)
Ответ: Вертикальная асимптота
(рис. 3)
Ответ: Вертикальная асимптота 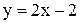 .
.