Переваги і додаткові можливості графіків передування

Оскільки стрілчасті графіки почали використовуватися раніше, у 50-х роках, а передування — у 60-х роках минулого століття, то природно, що свого часу перші набули більш значного поширення, особливо у нашій країні. Проте світова практика вказує на домінування сьогодні графіків передування з ряду причин:

Більш природним є зображення роботи у вигляді прямокутника.

Графіки передування легше створювати, оскільки спочатку можна зобразити всі прямокутники — роботи, а потім означити логічні зв’язки між ними. Це неможливо за використання стрілчастих графіків, де роботи позначаються вузлами початку і кінця, які зумовлюються логічними зв’язками.

Для графіків передування легше створювати комп’ютерні програми, які сьогодні використовують або тільки графіки передування, або обидва графіки — передування і стрілчастий з алгоритмом переходу від одного до другого.

Від графіків передування простіше перейти до діаграм Гантта, які є формою календарного планування.

Побудова графіків передування полегшується створенням WBS, оскільки спочатку визначаються всі роботи, а потім встановлюються логічні зв’язки між ними.

Ці графіки уможливлюють урахування частково паралельного виконання робіт.

Спинімося на цій властивості графіків передування докладніше.

У попередніх прикладах побудови сіткових графіків розглядався тільки один тип зв’язку між роботами, а саме тип «кінець — початок». Він передбачає, що наступна робота розпочинається після повного завершення попередньої. У реальному житті навіть послідовні роботи можуть виконуватися частково паралельно, що дозволяє скорочувати терміни виконання проекту. Якщо проілюструвати це на прикладі проекту організації комп’ютерного центру, то стає очевидним, що роботу з доставки і монтажу устаткування можна виконувати частково паралельно з підготовкою приміщення під це устаткування.

Залежно від сутності проектів діаграми передування дають змогу використовувати такі типи зв’язку між роботами:

1) кінець — початок (finish to start — F—S);

2) початок — початок (start to start — S—S);

3) кінець — кінець (finish to finish — F—F);

4) початок — кінець (start to finish — S—F);

5) гамак (Hammock — H).

1) кінець — початок (F—S) (рис. 6.11)

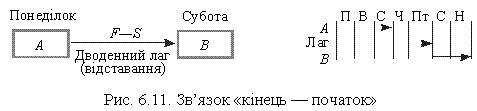
Це найпоширеніший тип зв’язку: робота В (наприклад, пробний запуск устаткування) не може розпочатися, поки не закінчиться робота А (монтаж устаткування). Якщо між роботами має бути перерва, то це вказується на графіку як лаг.

2) початок — початок (S—S) (рис. 6.12)

Ця схема демонструє зв’язок між датами початку двох робіт. Такий зв’язок використовується для скорочення термінів робіт перекриттям їх у часі. Вони пов’язані у випадку відстрочки початку роботи В. Наприклад, якщо робота А полягає у пофарбуванні підлоги у всіх кімнатах, а робота В — у монтажу меблів в одній із кімнат, то між початком першої і другої робіт повинно пройти чотири дні (з урахуванням часу на висихання підлоги у першій кімнаті).

3) кінець — кінець (F—F) (рис. 6.13)

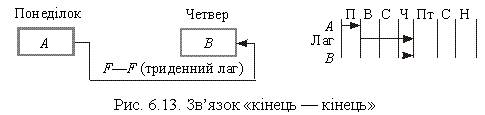
Ця схема демонструє зв’язок між завершенням двох робіт. Робота В має завершитися через три дні після закінчення роботи А (наприклад, виготовлення і фарбування конструкції: не можна фарбувати, поки не виготовлено, а на пофарбування треба чотири дні).

4) початок — кінець (S—F) (рис. 6.14)

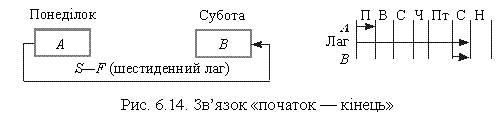
На цій схемі відображено зв’язок між початком А і кінцем В (щоб визначити сумарний термін виконання двох робіт). Наприклад, якщо автомобіль взяли напрокат на шість днів, то роботи з доставки у певний пункт і повернення мають бути закінчені у ці строки. Така залежність трапляється рідко.

5) гамак (Н)

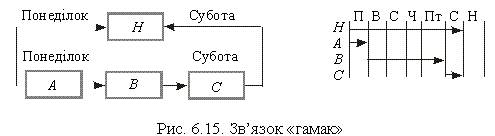
Цей тип зв’язку (рис. 6.15) використовується, аби поєднати кілька видів діяльності в одну, і застосовується для контролю по ключових точках (кінець етапу, а не окремі роботи). Наприклад, якщо в рамках виконання консультаційного проекту є етап виїзду на підприємство, який складається з робочої наради (робота А), зустрічей із фахівцями (робота В) і підсумкової для цього етапу зустрічі з керівництвом (робота С), то керівник проекту може розглядати його як одну роботу.

СІТКОВЕ ПЛАНУВАННЯ В УМОВАХ НЕВИЗНАЧЕНОСТІ

Оскільки характерною рисою проектів є їхня унікальність, то дуже часто буває складно визначити точно тривалість виконання окремих робіт, тому потрібно брати до уваги невизначеність термінів виконання окремих робіт проекту. Розгляньмо на прикладі, як це здійснюється.

Проект впровадження у виробництво нової продукції. Щоб розширити ринок збуту й одержати додаткові прибутки, підприємство вирішило розпочати виробництво тостера. Необхідні роботи та логічний зв’язок між ними показано у табл. 6.3. Кінцевий результат — доповідь з рекомендаціями стосовно організації виробництва і збуту цього товару.

Як бути з тривалістю виконання робіт? Якщо роботи повторюються у різних проектах, можна скористатися експериментальними або статистичними даними для одержання відповідних оцінок часу. Для абсолютно унікальних проектів тривалість робіт розглядається як випадкова змінна з відповідним розподілом імовірності.

Щоб урахувати ймовірність терміну виконання робіт, потрібно одержати три оцінки можливої тривалості для кожної роботи. Це:

оптимістичний час (а) — термін виконання роботи, якщо все буде забезпечено ідеально;

найбільш імовірний час (m) — очікуваний термін виконання роботи за нормальних умов;

песимістичний час (b) — термін виконання роботи, якщо виникнуть суттєві перешкоди.

Три оцінки часу дають змогу менеджеру висловити свої припущення щодо найбільш імовірного часу на виконання роботи і потім відобразити невизначеність, запропонувати кращий (оптимістичний) і гірший (песимістичний) варіант оцінки часу (табл. 6.4).

Повернімось до нашого прикладу. Очікуваний час виконання робіт обчислюється за формулою:

t = (a+4m+b)/6. [6.11]

Наприклад, для роботи А: t = (5+4+13)6 = 7 (тижнів).

Для визначення можливих коливань або мінливості цих значень використовуємо відому статистичну міру мінливості — дисперсію, або варіацію значень часу на виконання робіт:

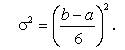
Значення очікуваного часу і варіацій наведені у табл. 6.4.

Як бачимо, чим більша різниця між оптимістичним і песимістичним часом, тим більше σ 2, тобто зростає ступінь невизначеності в оцінці тривалості робіт. Ці розрахунки базуються на припущенні, що невизначеність часу на виконання роботи можна отримати β -розподілом імовірності.

Проставляємо очікуваний час виконання робіт на сітковому графіку як фіксовані тривалості виконання робіт (рис. 6.16). Після цього визначаємо критичний шлях:

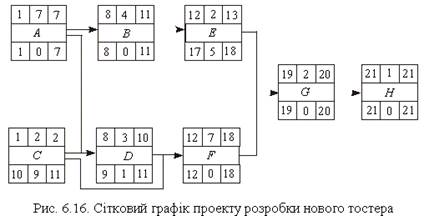
Критичний шлях — А — В — F — G — H.

Термін виконання — 21 тиждень.

Як впливатиме невизначеність в оцінках тривалості робіт на загальну тривалість виконання проекту?

Оскільки роботи критичного шляху визначають загальний термін виконання проекту, мінливість цих робіт впливатиме на мінливість часу виконання проекту в цілому. Інші роботи мають запас часу, і тому їх коливання не впливають на загальну тривалість.

Якщо позначити тривалість проекту в цілому як Т, то

Маючи цей розподіл, можемо обчислити ймовірність завершення проекту в установлені строки. Наприклад, якщо ми встановили Т  24 тижні, шукаємо значення Z=(24-21)/2.27=1.32.

Маючи таблицю нормального розподілу бачимо, що імовірність виконання проекту за 24 тижні становить 0, 8132. Таким чином, хоча зміна терміну виконання робіт може викликати збільшення строку завершення проекту, тобто перевищити 21 тиждень, можемо сподіватися на високу ймовірність завершення його скоріше ніж за 24 тижні.

Отже, сіткові графіки ми можемо використати для планування проектів з невизначеними оцінками часу виконання, оцінки тривалості проекту ймовірності завершення проекту в бажаний термін.