
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения типовых задач
|
|
Пример 1. Известно, что окисление оксида азота (NO) может протекать при взаимодействии с молекулярным кислородом и озоном. Рассчитайте время полувыведения оксида азота из приземного слоя атмосферного воздуха и определите, какой из этих процессов вносит основной вклад в окисление NO. Принять, что содержание молекул оксида азота в воздухе составляет 2∙ 109 см-3, а концентрация озона равна 15 млрд-1. Константы скоростей реакций окисления оксида азота кислородом и озоном равны соответственно: kк = 1, 93 ∙ 10-38 см6 ∙ моль-1∙ с-1 и kо = 1, 8 ∙ 10-14 см3 ∙ моль-1∙ с-1. Температура воздуха 150С, давление 101, 3 кПа.
Решение. Определим время полувыведения оксида азота из воздуха при его взаимодействии с молекулярным кислородом.
Процессу окисления соответствует уравнение: 2NO + O2 = 2NO2.
Скорость данной реакции: u(NO) = kк [O2] [NO]2,
где u(NO) – скорость процесса окисления NO, см-3 ∙ с-1; kк – константа скорости реакции третьего порядка, см6 ∙ с-1; [O2] и [NO] – концентрации кислорода и оксида азота в воздухе см-3.
Концентрация молекул кислорода в приземном слое воздуха равна 20, 95% (об.),
что составляет: [O2] = 2, 55∙ 1019 ∙ 20, 95/100 = 5, 34∙ 1018(см-3).
Т.к. количество молекул кислорода в воздухе значительно превосходит количество молекул оксида азота (т.е. [O2] = const), то скорость реакции окисления оксида азота можно представить как скорость реакции псевдо второго порядка: u(NO) = kк1 [NO]2
где kк1 – константа скорости реакции псевдо второго порядка, см3 ∙ моль-1∙ с-1;
kк1 = kк [O2] = 1, 93 ∙ 10-38 ∙ 5, 34∙ 1018 = 10, 31 ∙ 10-20 (см3 ∙ с-1).
Для реакций второго порядка период полувыведения, т.е. время, за которое концентрация исходных реагентов снизится в два раза, при условии равенства исходных концентраций реагентов: t1/2 = 1/ (kc),
где k – константа скорости реакции второго порядка, см3 ∙ с-1, с – концентрация исходного реагента, см-1.
В данной задаче: t1/2 = 1/ (kк1[NO]) = 1/ (10, 31 ∙ 10-20 ∙ 2∙ 109) = 4, 8 ∙ 109 (c) = 150(лет).
Время полувыведения оксида азота из приземного слоя воздуха в случае его взаимодействия с озоном. Уравнение реакции окисления NO озоном:
NO + O3 = NO2 + O2
Скорость данной реакции можно рассчитать по уравнению: u1 (NO) = ko [O3] [NO]
где u1 (NO) – скорость процесса окисления NO озоном, см-3 ∙ с-1; kо – константа скорости реакции второго порядка, см3 ∙ с-1; [O3] и [NO] – концентрации озона и оксида азота в воздухе см-3.
Концентрация молекул озона в приземном воздухе равна 15 млрд-1, тогда количество молекул озона в см3 при 15 0C (288 К) и нормальном атмосферном давлении:
[O3] = 2, 55∙ 1019∙ 15∙ 10-9 = 3, 82 ∙ 1011(см-3).
Т.к. концентрация озона более чем в сто раз превышает концентрацию NO, то С(О3) ≈ const. Тогда скорость реакции окисления NO озоном можно представить как реакцию псевдo первого порядка: u1 (NO) = ko1 [NO],
где kо1 – константа скорости реакции псевдо первого порядка,;
kо1 = kо [O3] = 1, 8 ∙ 10-14 ∙ 3, 82∙ 1011 = 6, 88 ∙ 10-3 (с-1).
Период полувыведения для реакций первого порядка: t1/2 = 0, 693/ k.
В данной задаче для реакции псевдо первого порядка:
t1/2 = 0, 693/ 6, 88 ∙ 10-3 = 100 (c) = 1, 7(мин).
Следовательно можно утверждать, что в приземном слое воздуха процесс окисления оксида азота связан в основном с окислением озоном.
Ответ: время полувыведения оксида азота при его взаимодействии с кислородом и озоном составляет 150 лет и 1, 7 мин соответственно. В приземном слое воздуха процесс окисления NO в основном притекает при участии озона.
Пример 2. Оцените молярное соотношение и общую массу диоксида серы и оксида азота, поступающих в атмосферу в течение суток с выбросами тепловой электростанции, работающей на угле. Содержание серы в угле равно 1, 5% (мас.). В сутки на станции сжигается 10 тыс. т угля. Концентрация оксида азота в газовых выбросах составляет 150 млн-1. Для сжигания угля используется стехиометрически необходимое количество воздуха. В расчетах принять, что уголь состоит из углерода и содержит в качестве примеси только серу.
Решение. Диоксид серы в выбросах отходящих газов при сжигании топлива появляется в результате окисления соединений серы, присутствующих в исходном топливе. Процесс может быть представлен уравнением:
S + O2 = SO2
Количество серы, сжигаемое на станции за сутки, составит:
m (S) = m(угля) ∙ α (S) = 10000 ∙ 0, 015 = 150 (т / сут),
где m(S) и m (угля) - массы серы и угля, сжигаемого на станции за сутки; α (S) – массовая доля серы в угле.
Количество молей диоксида серы, образующейся в результате сгорания угля, равно количеству молей серы, содержащейся в угле: n(SO2) = n(S) = m(S)/ M(S), где M(S) – молярная масса серы, г/моль.
n(SO2) = 150∙ 106/ 32 = 4, 69 ∙ 106 (моль/ сут).
Для вычисления количества молей оксида азота, образующегося в процессе горения угля, необходимо найти общее количество молей газов, содержащихся в отходящих продуктах (n общ). Количество молей оксида азота определяется количеством молей азота, содержащегося в воздухе, необходимом для окисления углерода и серы из угля, n(N2), количеством молей диоксида углерода, образующегося при горении углерода, - n(CO2) и количеством молей образующегося диоксида серы – n (SO2):
n общ = n (N2 ) + n(CO2) + n (SO2)
Процесс окисления углерода может быть представлен уравнением:
С + О2 = СО2
В сутки на станции сжигается 10000 т угля, в которых содержится 150 т серы и 10000 – 150 = 9850 т углерода. Количество молей углерода, сжигаемого в сутки на станции:
n(C) = m(C) / M (C) = 9850 ∙ 106 / 12 = 8, 21 ∙ 108 (моль/сут).
На каждый моль углерода образуется моль диоксида углерода и расходуется один моль кислорода из воздуха: n(CO2) = n(C) = 8, 21 ∙ 108 (моль/сут).
Общее количество молей кислорода, необходимое для окисления серы и углерода, содержащегося в угле:
n(O2) = n(O2 на окисление углерода) + n(O2 на окисление серы) =
= 4, 69 ∙ 106 + 8, 21 ∙ 108 = 8, 26 ∙ 108(моль/сут).
В процессе сжигания угля используется воздух, кислород из которого будет полностью израсходован на окисление углерода и серы, в отходящих газах останется лишь азот. Содержание азота в воздухе: n (N2) = n (O2) ∙ α (N2) / α (O2),
где α (N2) и α (O2), - содержание азота и кислорода в воздухе соответственно;
n(N2) = 8, 26 ∙ 108 ∙ 78, 11 / 20, 95 = 3, 08 ∙ 108 (моль/сут).
Общее количество молей газов в отходящих продуктах сжигания угля, составит:
nобщ. = 3, 08 ∙ 108 + 8, 26 ∙ 108 + 4, 69 ∙ 106 = 11, 34 ∙ 108 (моль/сут).
Количество молей оксида азота в отходящих газах:
n(NO) = α (NO) ∙ Nобщ.
где α (NO) – объёмная доля оксида азота в отходящих газах, по условию задачи равна 150∙ 10-6;
n(NO) = 150∙ 10-6 ∙ 11, 34 ∙ 108 = 1, 70 ∙ 105 (моль/сут).
Мольное соотношение диоксида серы и оксида азота в отходящих газах:
α n = n(SO2)/ n(NO) = 4, 69 ∙ 106 / (1, 70 ∙ 105) = 27, 6.
Массы диоксида серы и оксида азота, поступающих в атмосферу в процессе сжигания угля, можно определить из: m = n ∙ M,
где m – масса газа, г; n –содержание в отходящих газах, моль/сут; M – молярная масса соответствующего газа, г/моль;
m(SO2) = 4, 69 ∙ 106∙ 64 = 300∙ 106 (г /сут) = 300 (т /сут)
m(NO) = 1, 70 ∙ 105∙ 30 = 51∙ 105 (г /сут) = 5, 1 (т /сут)
Ответ: с отходящими газами тепловой станции в сутки в атмосферу поступает 300 т диоксида серы и 5, 1 т оксида азота; молярное соотношение диоксида серы и оксида азота равно 27, 6.
Пример 3. Какое максимальное количество молекул озона может образоваться в каждом кубическом сантиметре приземного воздуха при полном окислении метана в присутствии оксида азота. Если концентрация метана уменьшилась с 20 до 1, 6 млн-1. Давление равно 101, 3 кПа, температура воздуха 288 К.
Решение. При полном окислении метана в присутствии оксидов азота цепочку превращений можно представить суммарным уравнением:
СН4 + 8О2 + 4М → СО2 + 2Н2О + 4М* + 3О3.
При уменьшении концентрации метана в воздухе с 20 до 1, 6 млн-1 концентрация образовавшегося озона (если отсутствует его сток): [O3] = 4 ∙ (20 -1, 6) = 73, 6(млн-1).
В каждом кубическом сантиметре воздуха может образоваться n(O3) молекул озона:
n (O3) = NA∙ α (O3) ∙ T0 / (VM∙ 103 ∙ Tз) (см-3),
где NA – постоянная Авогадро; α (O3) – объёмная доля озона в воздухе: α (O3) = [O3] ∙ 10-6млн-1;
VM - молярный объём газа при нормальных условиях, л Т0 и Tз - температура воздуха при нормальных условиях и средняя у поверхности Земли (273 и 288 К соответственно);
n (O3) = 6, 02∙ 1023∙ 73, 6 ∙ 10-6 ∙ 273/(22, 4∙ 103∙ 288) = 19∙ 1014 (см-3).
Ответ: в каждом кубическом сантиметре воздуха может образоваться до 19∙ 1014 молекул озона.
Пример 4. Константа равновесия реакции образования оксида азота из азота и кислорода при 800 К равны 3∙ 10-11. Какого равновесного значения может достигнуть концентрация оксида азота в смеси, если исходная смесь – воздух?
Решение. Образование молекул оксида азота из азота и кислорода воздуха может быть представлен следующим уравнением: N2 + O2 = 2NO.
В процессе образования оксида азота не происходит изменения количества молей газов в смеси, константы равновесия при постоянном давлении и постоянной концентрации
КС и КР равны: КР = р(NO)2 / [р(N2) ∙ р(O2)],
где р(NO), р(N2) и р(O2) – парциальные давления NO, N2 и O2.
| Координата реакции | р(N2) | р(O2) | р(NO) |
| В начале процесса При равновесии Приближенное значение при равновесии | 79, 12 79, 12 - х 79, 12 | 22, 23 22, 23 - х 22, 23 | 2х 2х |
Поскольку константа равновесия процесса образования оксида азота мала, можно считать, что равновесные значения парциального давления NO будут низкими, поэтому парциальные давления азота и кислорода практически не изменятся. Поэтому можно воспользоваться приближенными равновесными значениями парциальных давлений компонентов смеси:
3∙ 10-11 = 4х2/ (79, 12∙ 22, 23);
р(NO) = 2x = 22, 97∙ 10-5 (кПа) = 0, 23 (Па).
Ответ: в воздухе при температуре 800 К равновесное парциальное давление оксида азота составляет 0, 23 Па.
Пример 5. Сравните скорости выведения из атмосферы молекул метана при их взаимодействии с гидроксильным радикалом на высотах 5 и 35 км. Концентрация метана изменяется от2 млн-1на высоте 5 км до 0, 6 млн-1 на высоте 35 км. Энергия активации и предэкпоненциальный множитель константы скорости реакции взаимодействия метана с ОН – радикалом равны14, 1 кДж/моль и 2, 3 см3• с-1 соответственно. Концентрация гидроксидных радикалов соответствуют средним для этих высот значениям:
[ОН]5 = 8, 5∙ 105 см-3 и [ОН]35 = 3∙ 107 см-3.
Решение. Взаимодействие метана с гидроксильным радикалом:
CH4 + OH· = CH3 + H2O.
Скорость данной реакции: uH = kH [CH4]H[OH]H,
где uH и kH - скорость и константа скорость реакции для условий, характерных для атмосферного воздуха на высоте Н; [CH4]H и [OH]H – концентрации молекул метана и гидроксильног радикала на высоте Н.
Константа скорости химической реакции зависит от температуры (уравнение Аррениуса): k = A ∙ e – E/ RT,
где k – константа скорости химической реакции (размерность определяется единицами измерения концентрации и времени, а также порядком химической реакции); А – предэкспоненциальный множитель (имеет размерность константы скорости реакции);
Е – энергия активации реакции, Дж/моль; R – универсальная газовая постоянная, Дж/(моль∙ К); T – температура реакции, К.
Скорость химической реакции будет определяться значениями концентраций реагентов и температурой воздуха на заданных высотах.
Температура воздуха на высоте 5 км: T5 = 288 + (- 6, 5 ∙ 5) = 256 (K),
на высоте 35 км: Т35 = 217 + (35 -11) ∙ 1, 38 = 250 (К).
Константа скорости реакции на высоте 5 км составляет:
k5 = 2, 3 exp { -14, 1∙ 103 / (8, 31 ∙ 256)} = 3, 04 ∙ 10 -3(см3∙ с-1), а на высоте 35 км:
k35 = 2, 3 exp { -14, 1∙ 103 / (8, 31 ∙ 250)} = 2, 59 ∙ 10 -3(см3∙ с-1).
Переведем заданные в условиях задачи значения концентраций молекул метана в см-3:
[ CH4]H = CH(млн-1) ∙ nH (см-3) ∙ 10-6,
где 10-6 – коэффициент пересчета концентрации, выраженной в млн-1 в объёмные доли;
nH – количество молекул в см3 воздуха на высоте заданной высоте.
Количество молекул в см3 воздуха на высоте 5 км:
N5 = 2, 55 ∙ 1019 exp[ Mg ∙ 5000 / (R∙ 256)],
где 2, 55 ∙ 1019 - количество молекул в кубическом сантиметре воздуха на уровне моря, см-3; M – средняя молярная масса воздуха равна 28, 96 ∙ 10-3 кг/моль; g - ускорение свободного падения, равно 9, 8 м / с2; 5000 – высота над уровнем моря, м; R – универсальная газовая постоянная, равна 8, 31 Дж /(моль ∙ К); 256 – температура воздуха на высоте 5 км, К.
n5 = 2, 55 ∙ 1019exp[-28, 96 ∙ 10-3 ∙ 9, 8 ∙ 5000 / (8, 31∙ 256)] = 1, 31 ∙ 1019(см-3).
Количество молекул в см3 воздуха на высоте 35 км:
n35 = 2, 55 ∙ 1019exp[-28, 96 ∙ 10-3 ∙ 9, 8 ∙ 35000 / (8, 31∙ 250)] = 2, 12 ∙ 1017(см-3).
Количество молекул метана в см3 на высоте 5 км составит:
[CH4]5 = 2∙ 1, 31 ∙ 1019 ∙ 10-6 = 2, 62∙ 1013 (см-3)..
на высоте 35 км:
[CH4]35 = 0, 6∙ 2, 12 ∙ 1017 ∙ 10-6 = 1, 27∙ 1011 (см-3).
Скорость химической реакции на высоте 5 км составит:
u5 = 3, 04 ∙ 10 -3 ∙ 2, 62∙ 1013∙ 8, 5∙ 105 = 6, 77 ∙ 1016(см-3∙ с-1),
на высоте 35 км: u35 = 2, 59 ∙ 10 -3 ∙ 1, 27∙ 1011∙ 3, ∙ 107 = 9, 86 ∙ 1015(см-3∙ с-1),
Отношение скоростей химических реакций взаимодействия метана с гидроксильным радикалом составит: u5/u35 = 6, 77∙ 1016/ 9, 86 ∙ 1015 = 6, 86.
Ответ: скорость процесса вывода метана из атмосферы при его взаимодействии с гидроксильным радикалом на высоте 5 км в 6, 86 раз выше, чем на высоте 35 км.
Пример 6. Константа скорости бимолекулярной реакции 2NO2 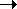 2NO + O2в условиях фотохимического воздействия при 627 К равна 1.81.103 см3/(моль. с).
2NO + O2в условиях фотохимического воздействия при 627 К равна 1.81.103 см3/(моль. с).
Вычислите истинную энергию активации и долю активных молекул, если диаметр молекулы NO2 можно принять равным 3.55 × 10 -8 см, а стерический множитель для этой реакции равен 0.019.
Решение. При расчете будем опираться на теорию активных столкновений:
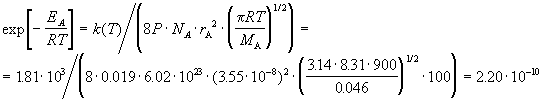 .
.
Это число представляет собой долю активных молекул.
При расчетах констант скорости с использованием различных теорий химической кинетики необходимо очень аккуратно обращаться с размерностями.
Обратите внимание на то, что радиус молекулы и средняя скорость выражены через см для того, чтобы получить константу в см3/(моль. с). Коэффициент 100 служит для перевода м/с в см/с.
Истинную энергию активации легко вычислить через долю активных молекул:
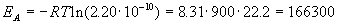 Дж/моль = 166.3 кДж/моль.
Дж/моль = 166.3 кДж/моль.