Рекурсия в ПРОЛОГе.

Рекурсия – это способ вычислений, в котором начальная задача сводится к последовательности подобных между собой задач, последняя из которых имеет непосредственное решение. Непосредственное решение задачи называется граничными условиями.

Хотя вычислительные задачи не являются сферой применения логического программирования, рассмотрим механизм рекурсии на примере вычисления факториала. В этом случае переход к подобной и более простой задаче осуществляется с помощью соотношения

n! =(n–1)! 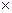n.

Непосредственным решением задачи (граничными условиями) является (0)! = 1, 1! = 1.

Введем предикат

fact: (integer, integer) procedure(i, o),

где первый аргумент имеет смысл n, а второй – результата, т.е. n!. На Прологе решение запишется так

class predicates
fact: (integer, integer) procedure(i, o).
clauses
classInfo(" factorial", " 1.0").
fact(0, 1): -!.
fact(N, R): -M=N-1, fact(M, R1), R=R1*N.
run(): -
console:: init(), stdio:: write(" Input number: "), fact(stdio:: read(), R), stdio:: nl,
stdio:: write(" Factorial is ", R).

В результате рекурсивных вызовов содержимое стека будет формироваться в следующем порядке (снизу вверх)

Фаза редукции Фаза решения

R₃ =3 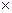R₂ R₃ =3 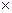2=6

R₂ =2 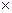R₁ R₂ =2 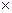1=1

R₁=1 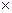R₀ R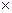₁ =1 1=1

R₀ =1

Для данной задачи существенным есть место граничного условия. Если бы оно было расположено на последнем месте, то правило должно было бы быть сформулировано так

factor (N, R): - M=N-1, M> =0, factor (M, Rm), R=N*Rm.

factor (0, 1).

В противоположном случае сложилась бы ситуация с неограниченными вычислениями, так как граничное условие никогда бы не достигалось, поскольку в какой-то момент переменная стала бы отрицательной. Важным есть также применение новой переменной для вычисления (n-1)!. Применение старой переменной приводит к проверке истинности условия N=N-1, которое заведомо является ошибочным.

Рассмотрим еще один пример рекурсивных вычислений. Пусть надо найти сумму первых членов ряда

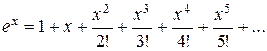
На первый взгляд это легко сделать с помощью двух предикатов, один из которых будет вычислять факториал, а второй – степенную функцию. Но, если учесть, что

,

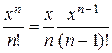то каждое слагаемое в сумме тоже будет исчисляться рекурсивно, и задача может быть разрешима в пределах одного предиката. Образуем предикат

sum_n: (real, integer, real, real) procedure (i, i, o, o),

аргументы которого имеют следующий смысл: переменная 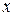, число слагаемых, результат, рабочий параметр. Граничное условие будет иметь вид

sum_n(_, 0, 1, 1),

а сам предикат запишется так

sum_n(X, N, R, W): -M=N-1, sum_n(X, M, R1, W1), W=W1*X/N, R=R1+W.

Его вызовом будет, например

? sum_n(0.2, 4, Z, _).

Если изменить формулировку задачи таким образом, чтобы надо было найти эту сумму с определенной точностью, то строение соответствующего предиката и ход вычислений существенно изменятся. Пусть степенью точности является условие, что последний член суммы по абсолютной величине не превосходит заданной погрешности. В этом случае движение к граничному условию будет осуществляться не путем уменьшения (нисходящая рекурсия), а, наоборот, ее необходимо совместить с целевым утверждением. Тогда предикат и вызов примут вид

sum_e(X, N, R, Rout, W, E): - abs(W)> E, M=N+1, W1=W*X/M, R1=R+W1,

sum_e(X, M, R1, Rout, W1, E).

sum_e(_, _, R, R, W, E): -abs(W)< E.

? sum_e(0.2, 0, 1, Z, 1, 0.001).

Здесь аргументы R, Rout, E – имеют соответственно смысл известной суммы, искомой суммы и погрешности.

ПРИМЕР 1. Возведение в степень .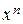

class predicates

power: (real, integer, real) procedure(i, i, o).

clauses

power(_, 0, 1): -!.

power(X, N, R): - M=N-1, power(X, M, R1), R=R1*N.

run(): -console:: init(), power(srdio:: read(), stdio:: read(), R), stdio:: write(R).