Лабораторная работа №7. Тема: «Вычисление функций одной переменной в Excel»

Тема: «Вычисление функций одной переменной в Excel»

Цель занятия: получить практические навыки вычисления функций одной переменной у=f(x) и построения их графиков в Excel

Отрабатываемые вопросы:

1.Создание формул для вычисления функций одной переменной.

2.Построение графиков функций.

Организационно – методические указания

В Excel удобно осуществлять построение различных функций на плоскости и поверхностей в пространстве.

1 .Построение прямой. Рассмотрим построение данной функции в Excel на примере уравнения у=2х+1 в диапазоне: хÎ [0; 3] с шагом х=0, 25. Решение з адачи включает следующие этапы.

1.1. Ввод данных. Для этого значения аргумента Х и функции У следует представить в таблице, первый столбец которой будет заполнен значениями Х, а второй – функцией У. Для этого в ячейку А1 вводим заголовок Аргумент, а в ячейку В1 – заголовок Прямая.

В ячейку А2 вводится первое значение аргумента 0, а в ячейку A3 вводится второе значение аргумента с учетом шага построения (0, 25). Затем, выделив блок ячеек А2: АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).

Далее вводим уравнение прямой: в ячейку В2 вводим формулу: =2*A2+1, з атем копируем эту формулу в ячейки В2: В14. В результате должна быть получена следующая таблица исходных данных и результатов (рис.1.).

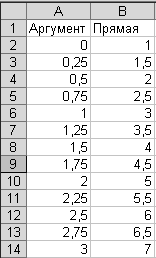
Рис.1.Построение прямой

1.2. Построение графика функции. Выделите диаграмму и, используя вкладку Вставка ® График, постройтеграфик функции у=2х+1 (рис.2.).

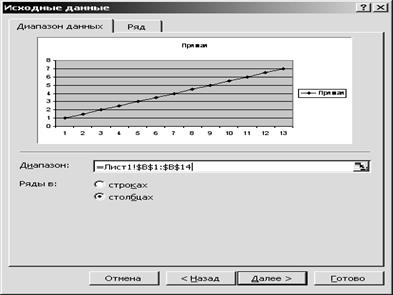
Рис.2. График прямой

1.3. Используя в кладку Макет, выполните самостоятельно оформление полученного графика (название графика и осей, размещение легенды и т.п.).

2. Решение уравнения второго порядка. Примерами уравнений второго порядка являются: парабола, гипербола, окружность, эллипс и другие. В качестве примера рассмотрим построение параболы вида: у =х² в диапазоне хÎ [–3; +3] с шагом х=0, 5.

2.1. Ввод данных.В ячейку А2 вводится первое значение аргумента (-3), в ячейку A3 вводится второе значение аргумента (–2, 5), а затем, выделив блок ячеек А2: АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).

Далее в ячейку В2 вводим уравнение =А2*А2, а затем копируем эту формулу в диапазон В2: В14. В результате должна быть получена следующая таблица исходных данных.

2.2.Построение графика функции. Используя вкладку Вставка ® ДИАГРАММА, постройтеграфик функции у=х^2 (РИС.4).

Используя в кладку Макет, выполните самостоятельно оформление полученного графика (название графика и осей, размещение легенды и т.п.).

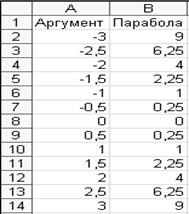
Рис.3. Построение параболы

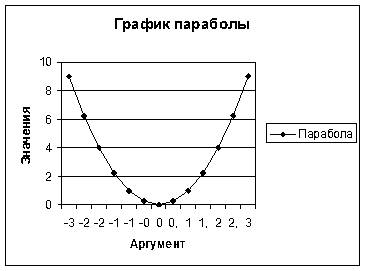
Рис.4.График параболы

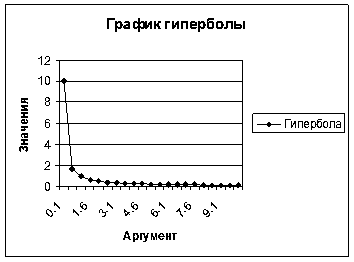
Рис.5. График гиперболы

3. Построение гиперболы. В простейшем случае уравнение гиперболы имеет вид y=k/x. Задача построения гиперболы аналогична построению параболы.

Рассмотрим построение гиперболы y=1/x в диапазоне хÎ [0, 1: 10, 1] с шагом х=0, 5. Выполните все вышеуказанные действия самостоятельно (рис.5).