Методика факторного анализа. Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи и взаимообусловленности

Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи и взаимообусловленности. Одни из них непосредственно связаны между собой, другие косвенно. Отсюда важным методологическим вопросом в экономическом анализе является изучение и измерение влияния факторов на величину исследуемых экономических показателей.

Под экономическим факторным анализом понимается постепенный переход от исходной факторной системы к конечной факторной системе, раскрытие полного набора прямых, количественно измеримых факторов, оказывающих влияние на изменение результативного показателя.

По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа.

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.

Основные свойства детерминированного подхода к анализу:

- построение детерминированной модели путем логического анализа;

- наличие полной (жесткой) связи между показателями;

- невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;

- изучение взаимосвязей в краткосрочном периоде.

Различают четыре типа детерминированных моделей:

Аддитивные модели представляют собой алгебраическую сумму показателей и имеют вид

.

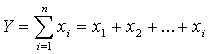К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях.

Мультипликативные модели в обобщенном виде могут быть представлены формулой

.

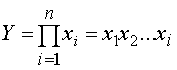Примером мультипликативной модели является двухфакторная модель объема реализации:

,

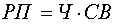где Ч - среднесписочная численность работников;

CB - средняя выработка на одного работника.

Кратные модели:

.

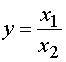Примером кратной модели служит показатель срока оборачиваемости товаров (в днях) ^. Т_ОБ.Т:

,

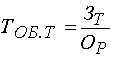где З_Т - средний запас товаров; О_Р - однодневный объем реализации.

Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

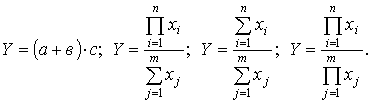
Примерами таких моделей служат показатели затрат на 1 руб. товарной продукции, показатели рентабельности и др.

Для изучения зависимости между показателями и количественного измерения множества факторов, повлиявших на результативный показатель, приведем общие правила преобразования моделей с целью включения новых факторных показателей.

Для детализации обобщающего факторного показателя на его составляющие, которые представляют интерес для аналитических расчетов, используют прием удлинения факторной системы.

Если исходная факторная модель 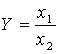, а 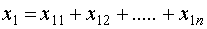, то модель примет вид .

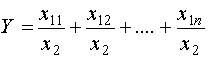Для выделения некоторого числа новых факторов и построения необходимых для расчетов факторных показателей применяют прием расширения факторных моделей. При этом числитель и знаменатель умножаются на одно и тоже число:

.

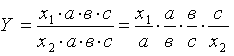Для построения новых факторных показателей применяют прием сокращения факторных моделей. При использовании данного приема числитель и знаменатель делят на одно и то же число.

.

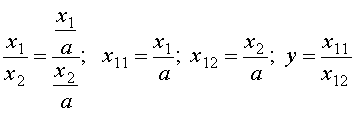Детализация факторного анализа во многом определяется числом факторов, влияние которых можно количественные оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели. В основе их построения лежат следующие принципы:

- место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя;

- модель должна строиться из двухфакторной полной модели путем последовательного расчленения факторов, как правило качественных, на составляющие;

- при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены.

Построение факторной модели – первый этап детерминированного анализа. Далее определяют способ оценки влияния факторов.

Способ цепных подстановок заключается в определении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать – значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. При этом исходя из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения. потом изменяются два при неизменности остальных и т.д.

В общем виде применение способа цепных постановок можно описать следующим образом:

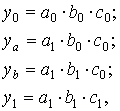
где a₀, b_0, c₀ - базисные значения факторов, оказывающих влияние на обобщающий показатель у_;

a₁, b₁, c₁ - фактические значения факторов;

y_a, y_b, - промежуточные изменения результирующего показателя, связанного с изменением факторов а, b, соответственно.

Общее изменение Dу=у₁–у₀ складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

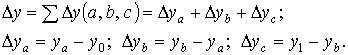
Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора.

Однако существуют определенные правила, определяющие последовательность подстановки:

- при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;

- если модель представлена несколькими количественными и качественными показателями, последовательность подстановки определяется путем логического анализа.

Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).

Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.).

Способ абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:

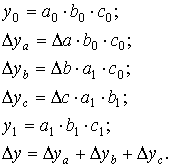
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида у = (а – в) ^. с. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.

Для мультипликативных моделей типа у = а ^. в ^. с методика анализа следующая:

· находят относительное отклонение каждого факторного показателя:

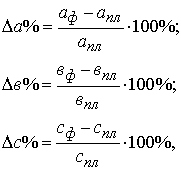
· определяют отклонение результативного показателя у за счет каждого фактора

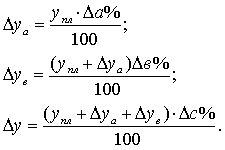
Результаты расчетов те же, что и при использовании предыдущего способа.

Интегральный метод позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, т.к. в нем действует логарифмический закон перераспределения факторных нагрузок. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.

Можно использовать также уже сформированные рабочие формулы, приводимые в специальной литературе [4]:

1. Модель вида :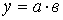

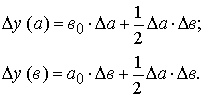
2. Модель вида :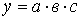

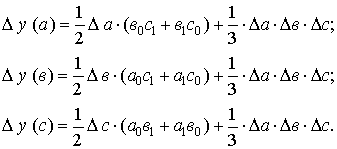
3. Модель вида :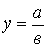

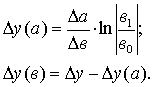
4. Модель вида :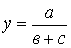

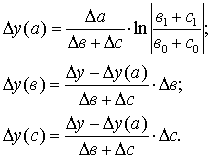
Рассмотрим возможность использования основных методов детерминированного анализа, обобщив вышеизложенное в виде матрицы (табл.2).

Таблица 2

Матрица применения способов детерминированного факторного анализа

Модели Способы	Мультипликативные	Аддитивные	Кратные	Смешанные
Цепной подстановки	+	+	+	+
Абсолютных разниц	+	-	+	-
Относительных разниц	+	-	-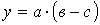
Интегральный	+	-	+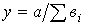

Вопросы для самоконтроля

1. Какие задачи управления решаются посредством экономического анализа?

2. Охарактеризуйте предмет экономического анализа.

3. Какие отличительные особенности характеризуют метод экономического анализа?

4. Какие принципы лежат в основе классификации приемов и способов анализа?

5. Какую роль в экономическом анализе выполняет способ сравнения?

6. Объясните способы построения детерминированных факторных моделей.

7. Опишите алгоритм применения наиболее простых способов детерминированного факторного анализа: способа цепных подстановок, способа разниц.

8. Охарактеризуйте достоинства и опишите алгоритм применения интегрального метода.

9. Приведите примеры задач и факторных моделей, к которым применяется каждый из методов детерминированного факторного анализа.