
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Криптоанализ шифра простой однобуквенной замены
|
|
Задание: дешифровать шифр простой однобуквенной замены (используемый алфавит состоит из 32-х русских букв («ё» принимается за «е», прописные и строчные буквы не различаются), тексты по вариантам).
Теория
Пусть алфавит состоит из 32-х русских букв («ё» принимается за «е», прописные и строчные буквы не различаются):
| Символ | а | б | в | г | д | е | ж | з | и | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ъ | ы | ь | э | ю | я |
| № |
Шифрование заключается в выборе некоторой перестановки на множестве букв алфавита (перестановка является ключом шифра) и замене букв открытого текста с номером i на букву перестановки с тем же номером. Например, зашифруем фрагмент известного высказывания великого русского учёного Михаила Васильевича Ломоносова «Математику уже затем учить надо,
что она ум в порядок приводит» перестановкой
| Символ | л | о | м | н | с | в | а | б | г | д | е | ж | з | и | й | к | п | р | т | у | ф | х | ц | ч | ш | щ | ъ | ы | ь | э | ю | я |
| № |
| м | а | т | е | м | а | т | и | к | у | у | ж | е | з | а | т | е | м | у | ч | и | т | ь | н | а | д | о | , | ч | т | о | … | |||||
| з | л | т | в | з | л | т | г | е | у | у | а | в | б | л | т | в | з | у | ч | г | т | ь | и | л | с | й | , | ч | т | й | … |
Любой метод вскрытия шифра простой однобуквенной замены основан на том обстоятельстве, что с точностью до переобозначений частотные характеристики m -грамм шифртекста и открытого текста одинаковы. При этом существенно используются априорные частотные характеристики предполагаемого открытого текста, получаемые с учетом «характера переписки». Такие характеристики являются более «рельефными» для литературных текстов и менее «рельефными» для формализованных электронных текстов. Чем менее рельефно распределение знаков текста, тем сложнее задача вскрытия шифра простой замены. Для открытых текстов с «почти равномерным» распределением знаков эта задача становится практически не решаемой (см. Алферов и др. «Криптографические методы защиты информации», п. 5.2).
Далее мы будем решать задачу вскрытия простой замены лишь при условии, что предполагаемые открытые тексты — это литературные тексты. Кроме того, мы будем считать, что при дешифровании мы располагаем достаточно большим числом знаков шифртекста. чтобы опираться на «статистику».
Алгоритм вскрытия простой замены по тексту криптограммы достаточно сложно формализовать. При любой попытке формализации теряется какой-нибудь важный нюанс. Поэтому мы укажем лишь основные идеи, лежащие в основе такого алгоритма. Обычно выделяют следующие этапы алгоритма:
Алгоритм 1
1. Подсчет частот встречаемости шифробозначений, а также некоторых их сочетаний, например биграмм и триграмм подряд идущих знаков.
2. Выявление шифробозначений, заменяющих гласные и согласные буквы.
3. Выдвижение гипотез о значениях шифробозначений и их проверка. Восстановление истинного значения шифробозначений.
Если длина текста достаточно велика, то найденные на этапе 1 частоты окажутся близкими к табулированным значениям частот знаков (соответственно — биграмм или триграмм). Проведенная на этом этапе работа служит основанием для выдвижения гипотез о значениях шифрвеличин, соответствующих данным шифробозначениям. При этом учитывается, что каждая буква имеет группу предпочтительных связей (наиболее вероятных сочетаний её с другими буквами), которые составляют ее наиболее характерную особенность. Как правило, такие гипотезы подтверждаются не полностью. Хорошим критерием при этом является «читаемость» восстанавливаемого открытого текста. Важно также учитывать процентное соотношение количества гласных и согласных в открытом тексте
и прочие их характеристики, например:
- если шифробозначение часто встречается, равномерно располагается по шифртексту, в отдельных местах чередуется через 1, 2 или 3 знака, сочетается с средними и редкими (по частоте) шифробозначениями, то это дает основания полагать, что такое шифробозначение скрывает гласную букву;
- удвоение гласных в открытом тексте происходит реже, чем согласных;
- если некоторое шифробозначение признано гласной, то буква, часто сочетающаяся с ней, скорее всего согласная;
- в открытом тексте чрезвычайно редко встречаются три, и более, подряд идущие гласные;
- четыре, и более, подряд идущие согласные также редки и т. д. (см. Алферов и др. «Криптографические методы защиты информации», Приложение 1).
Если с помощью приведенных соображений произведено несколько идентификаций шифробозначений, то дальнейшая работа по вскрытию текста криптограммы не представляет особого труда. Пример вскрытия шифра простой однобуквенной замены по алгоритму 1 приведен в (Алферов и др. «Криптографические методы защиты информации», Приложение 2).
Наиболее трудно формализуемым фрагментом алгоритма 1 является проверка выдвигаемых гипотез о значениях шифробозначений. Трудность состоит в формулировке критерия, подтверждающего или отвергающего ту или иную гипотезу. В (см. Алферов и др. «Криптографические методы защиты информации», п. 5.2) со ссылкой на автора изложен один из способов четкой формализации критерия, основанный на “близости” матрицы биграмм 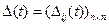 (где n — число букв алфавита) данного текста t эталонной матрице биграмм
(где n — число букв алфавита) данного текста t эталонной матрице биграмм 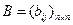 открытого текста. Приведем эту идею и основанный на ней эвристический алгоритм дешифрования.
открытого текста. Приведем эту идею и основанный на ней эвристический алгоритм дешифрования.
Мерой близости служит следующая «целевая функция» f (t), связывающая матрицы 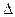 (t) и b:
(t) и b:
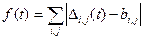 .
.
Будем исходить из того естественного предположения, что если у — данная криптограмма и Dk — правило расшифрования на ключе k данного шифра простой замены, то для истинного ключа ku, значение
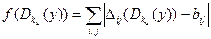
должно быть минимальным.
Идея основного шага алгоритма состоит в том, чтобы исходя из некоторого первичного “приближения” k для ключа ku, основанного, например, на диаграмме частот букв, немного его изменять неким «разумным» способом, уменьшая значение целевой функции f (t).
Приведем теперь формальное описание алгоритма.