Схема дисперсионного анализа.

Средние квадраты и s_R² представляют собой несмещенные оценки зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной х и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров регрессии, n – число наблюдений. При отсутствии линейной зависимости между зависимой и объясняющей (факторной) переменной случайные величины и s_R² имеют 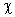² – распределение соответственно с m-1 и n-m степенями свободы, а их отношение F – распределение с теми же степенями свободы. Поэтому, уравнение регрессии значимо на уровне , если фактически наблюдаемое значение статистики превышает табличное:

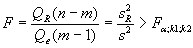(5.11),

где 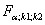- табличное значение F – критерия Фишера – Снедекора, определенное на уровне значимости при k1 = m-1 и k2 = n-m степенях свободы.

Учитывая смысл величин и s_R², можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.

В случае парной линейной регрессии m = 2, и уравнение регрессии значимо на уровне , если

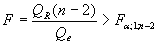(5.12)

Мерой значимости линии регрессии может служить следующее соотношение:

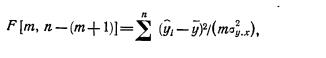
где ŷ _i—i-e выравненное значение; 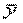—средняя арифметическая значений y_i; σ _y.x—средняя квадратическая ошибка (ошибка аппроксимации) регрессионного уравнения, вычисляемая по известной формуле; n—число сравниваемых пар значений признаков; m—число факторных признаков.

Действительно, связь тем больше, чем значительнее мера рассеяния признака, обусловленная регрессией, превосходит меру рассеяния отклонений фактических значений от выравненных.

Данное соотношение позволяет решить вопрос о значимости уравнения регрессии в целом, то есть о наличии реально существующей статистической зависимости между переменными. Уравнение регрессия значимо, т. е. между признаками существует статистическая связь, если для данного уровня значимости расчетное значение критерия Фишера F[m, n-(m+1)] превышает критическое значение F_кр[m, n-(m+1)], стоящее на пересечении m-го столбца и [n—(m+1)]-й строки специальной статистической таблицы, которая так и называется «Таблица значений F-критерия Фишера».

Пример. Воспользуемся критерием Фишера для оценки значимости уравнения регрессии, построенного на прошлой лекции, то есть уравнения, выражающего зависимость между сбором урожая и размером посева на душу населения.

Подставив в формулу для расчета критерия Фишера, данные предыдущего примера, получим

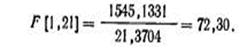
Обращаясь к таблице F-распределения для Р=0, 95 (α =1—Р=0, 5) и учитывая, что n-2=21, m-1 =1, в таблице значений F-критерия на пересечения 1-го столбца и 21-й строки находим критическое значение F_кр, равное 4, 32 при степени надежности Р=0, 95. Поскольку расчетное значение F-критерия существенно превосходит по величине F_кр, то обнаруженная линейная связь существенна, т. е. априорная гипотеза о наличии линейной связи подтвердилась. Вывод сделан при степени надежности P=0, 95. Можно проверить, что вывод в данном случае останется прежним, если надежность повысить до Р=0, 99 (соответствующее значение F_кр=8, 02 для уровня значимости α =0, 01).

Коэффициент детерминации. С помощью F-критерия мы установили, что существует линейная зависимость между величиной сбора хлеба и величиной посева на душу. Следовательно, можно утверждать, что величина сбора хлеба, приходящегося на душу, линейно зависит от величины посева на душу. Теперь уместно поставить уточняющий вопрос — в какой степени величина посева на душу определяет величину сбора хлеба на душу? На этот вопрос можно ответить, рассчитав, какая часть вариации результативного признака может быть объяснена влиянием факторного признака. Этой цели служит индекс (или коэффициент) детерминации R², который позволяет оценить долю разброса, учитываемого регрессией, в общем разбросе результативного признака. Коэффициент детерминации, равный отношению факторной вариации к полной вариации признака, позволяет судить о том, насколько «удачно» выбран вид функции, описывающей реальную статистическую зависимость.

Если известен коэффициент детерминации R², то критерий значимости уравнения регрессии или самого коэффициента детерминации (критерий Фишера) может быть записан в виде:

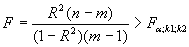
Критерий Фишера позволяет также оценивать полезность включения дополнительных факторов в модель для уравнения множественной линейной регрессии.

Пример. Оценить полезность включения в уравнение регрессии дополнительной переменной «урожайность» (по данным и результатам ранее рассмотренных примеров).

Разброс признака, объясняемый уравнением множественной регрессии и рассчитываемый как сумма квадратов разностей выравненных значений и их средней, равен 1623, 8815. Разброс признака, объясняемый уравнением простой регрессии, составляет 1545, 1331.

Разброс признака, регрессией не объясняемый, определяется квадратом средней квадратической ошибки уравнения и равен 10, 9948.

Воспользовавшись этими характеристиками, рассчитаем частный F-критерий

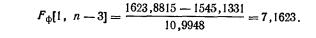
С уровнем надежности 0, 95 (α =0, 05) табличное значение F (1, 20), т. е. значение, стоящее на пересечении 1-го столбца и 20-й строки табл. 4А приложения, равно 4, 35. Рассчитанное значение F-критерия значительно превосходит табличное, и, следовательно, включение в уравнение переменной «урожайность» имеет смысл.

Таким образом, выводы, сделанные ранее относительно коэффициентов регрессии, вполне правомерны.

4й учебный вопрос. Оценка значимости отдельных параметров уравнения регрессии с помощью критерия Стьюдента.

Очень часто в эконометрике требуется оценить значимость коэффициента корреляции r, то есть определить, насколько существенно отличие коэффициента корреляции от нуля (например, при анализе мультиколлинеарности и оценке парных коэффициентов корреляции между факторами в уравнении множественной регрессии).

При этом исходят из того, что при отсутствии корреляционной связи статистика t,

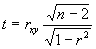
имеет t -распределение Стьюдента с (n-2) степенями свободы.

Коэффициент корреляции r_xy значим на уровне , (иначе – гипотеза Н₀ о равенстве генерального коэффициента корреляции нулю отвергается), если

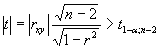(5.13),

где 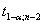-табличное значение t -критерия Стьюдента, определенное на уровне значимости a при числе степеней свободы (n-2).

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка. Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется значение t-критерия, его величина сравнивается с табличным значением при (n-2) степенях свободы. Проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

Заключение. Итак, мы рассмотрели на данной лекции общие правила проверки статистических гипотез и их практическое применение при оценке значимости уравнений регрессии и их отдельных параметров с помощью критериев Фишера и Стьюдента.