
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод цепей и сечений
|
|
Комбинационная релейно-контактная схема имеет вид:
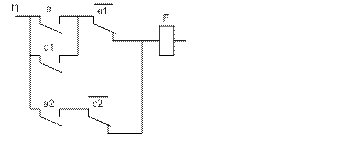
Под сечение понимается набор состояния контактов, которые обеспечивают разрыв всех цепей схемы. В нашей схеме четыре сечения
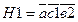
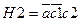
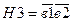
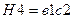 Перечисление всех цепей и сечение однозначно задаёт схему. Под цепью, урезанной на контакте а понимается набор состояний контактов, соответствующей данной цепи, из которого исключено состояние контакта а. Из цепи G1 можно образовать 2 урезанные цепи: на контакте а и на контакте с:
Перечисление всех цепей и сечение однозначно задаёт схему. Под цепью, урезанной на контакте а понимается набор состояний контактов, соответствующей данной цепи, из которого исключено состояние контакта а. Из цепи G1 можно образовать 2 урезанные цепи: на контакте а и на контакте с: 
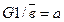 . Аналогично можно сделать и для других контактов.
. Аналогично можно сделать и для других контактов. 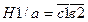
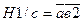 и так далее. Для того, чтобы проверить некоторый контакт а на отсутствие неисправность типа разрыв необходимо обеспечить наличие какой-либо цепи, содержащеё этот контакт и обрыв всех других цепей, в которые не входит данный контакт, тогда при отсутствии неисправности схема будет замкнута, а о наличии неисправность будет свидетельствовать разомкнутое состояние схемы. Для проверки на разрыв контакта а необходима создать цепь G1 и разорвать все другие цепи. G1 мы разрываем контактом с1, а G3 можно разорвать на любом из её контактов, тогда при разрыве контакта а схема будет находиться в разомкнутом состоянии вместо замкнутого, чем и будет зафиксирована неисправность. Условие обнаружения неисправности типа разрыв контакта а выполняется, если на входы схемы подаётся такой набор входных переменный, при котором обеспечивается одновременное существование хотя бы одной цепи, содержащеё контакт а и хотя бы одного сечения, урезанного на контакте а. При проверке некоторого контакта а на отсутствие неисправности типа короткое замыкание необходимо обеспечить разрыв всех цепей схемы и наличие хотя бы одной цепи, разорванной только в данном контакте, тогда при отсутствии неисправностей схема будет разомкнутой, а о наличии неисправностей будет свидетельствовать замкнутое состояние схемы. Для проверки контакта с1 на короткое замыкание необходимо обеспечить разрыв цепи G2 только в контакте с1, а разрыв остальных цепе на любых контактах, тогда при коротком замыкании контактов с1 из всех цепей замкнётся только цепьG2, в следствии чего схема будет находиться в замкнутом состоянии, вместо разомкнутого, что будет свидетельствовать о неисправности с1. Условия обнаружения неисправности типа короткое замыкание контакта а выполняется, если на входы системы подается такой набор входных переменных, при котором обеспечивается одновременно существование сечения, содержащего контакт а, и цепи, урезанной на контакте а. В алгоритм вычисления проверяющей функции контакта а для неисправности типа разрыв будем писать
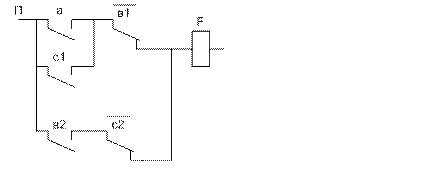
и так далее. Для того, чтобы проверить некоторый контакт а на отсутствие неисправность типа разрыв необходимо обеспечить наличие какой-либо цепи, содержащеё этот контакт и обрыв всех других цепей, в которые не входит данный контакт, тогда при отсутствии неисправности схема будет замкнута, а о наличии неисправность будет свидетельствовать разомкнутое состояние схемы. Для проверки на разрыв контакта а необходима создать цепь G1 и разорвать все другие цепи. G1 мы разрываем контактом с1, а G3 можно разорвать на любом из её контактов, тогда при разрыве контакта а схема будет находиться в разомкнутом состоянии вместо замкнутого, чем и будет зафиксирована неисправность. Условие обнаружения неисправности типа разрыв контакта а выполняется, если на входы схемы подаётся такой набор входных переменный, при котором обеспечивается одновременное существование хотя бы одной цепи, содержащеё контакт а и хотя бы одного сечения, урезанного на контакте а. При проверке некоторого контакта а на отсутствие неисправности типа короткое замыкание необходимо обеспечить разрыв всех цепей схемы и наличие хотя бы одной цепи, разорванной только в данном контакте, тогда при отсутствии неисправностей схема будет разомкнутой, а о наличии неисправностей будет свидетельствовать замкнутое состояние схемы. Для проверки контакта с1 на короткое замыкание необходимо обеспечить разрыв цепи G2 только в контакте с1, а разрыв остальных цепе на любых контактах, тогда при коротком замыкании контактов с1 из всех цепей замкнётся только цепьG2, в следствии чего схема будет находиться в замкнутом состоянии, вместо разомкнутого, что будет свидетельствовать о неисправности с1. Условия обнаружения неисправности типа короткое замыкание контакта а выполняется, если на входы системы подается такой набор входных переменных, при котором обеспечивается одновременно существование сечения, содержащего контакт а, и цепи, урезанной на контакте а. В алгоритм вычисления проверяющей функции контакта а для неисправности типа разрыв будем писать 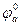 , выписываются все цепи, содержащие контакт а,
, выписываются все цепи, содержащие контакт а,
выписываются все сечения, содержащие контакта, определяются все сечения, урезанные на контакте а. Каждую выписанную цепь рассматривают в сочетании с каждым урезанным сечением. Для них определяют входные наборы, на которых они одновременно существуют, проверяющую функцию фи а ноль находят, как объединение всех входных наборов.
30 Алгоритм вычисления проверяющей функции φ a1(φ a0)
Алгоритм вычисления проверяющей функции для короткого замыкания фи а единица аналогичен, только термин «цепь» необходимо заменить на термин сечение. Для контакта a в схеме определить φ a0. Контакт a входит в цепь G1 и в сечения Н1 и Н2. Находим урезанные сечения Н1/а=не(с1)ь2, Н2/а=не(с1)с2. Рассмотрим сочетание цепи G1=aне(ь1) с сечением Н1/а=не(с1)ь2. Цепь существует при подаче входных переменных а=1 и ь=0, сечение существует при вх переменных с=0 ь=0. Указанные условия не противоречат друг другу. Цепь G1 и урезанное сечение Н1 одновременно существует на наборе а, в инверсное, с инверсное. Рассмотрим сочетание цепи G1 и Н2/а. Последнее не может быть обеспечено, так как в нём содержаться противоречия. Переменная с одновременно должна принимать и прямое и переменное значение. 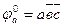 . Для контакта ь1 определяем
. Для контакта ь1 определяем 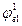 . Он входит в сечения Н3=Ь1не(Ь2)
. Он входит в сечения Н3=Ь1не(Ь2)
Н4=Ь1с2 и в цепи G1=aне(ь1) и G2=c1не(b1) Находим урезанные цепи: G1 / b1=a и
G2/ b1=c1. Сечение H3=не(b1b2) не рассматриваем, так как оно содержит в себе
противоречие. Сечение Н4 и цепь G1/b1 одновременно существуют на наборе abc. Для одновременного существования сечения Н4 и цепи G2/b1 достаточно установить переменные Ь=1 и с=1. Переменная а может принимать любое значение. Поэтому данное сочетание дает два набора: abc и аЪс {которое уже получено). Таким образом, 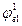 =abc+abc=bc.
=abc+abc=bc.