
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задания контрольной работы
|
|
по дисциплине «Экономико-математические методы в логистике»
Задание 1. Найти экстремум целевой функции
L (x) = c 1 x 1+ c 2 x 2 ® max (min)
 при ограничениях:
при ограничениях:
a 11 x 1 + a 12 x 2 £ b 1,
a 21 x 1 + a 22 x 2 £ b 2,
a 31 x 1 + a 32 x 2 £ b 3,
a 41 x 1 + a 42 x 2 £ b 4,
x 1, 2 ³ 0.
Значения коэффициентов целевой функции и системы ограничений
| N варианта | ||||||||||
| Значения | ||||||||||
| c 1 | -1 | -2 | -1 | -1 | ||||||
| c2 | -2 | -1 | -1 | |||||||
| a 11 | -1 | -3 | -1 | -2 | ||||||
| a 12 | -2 | -2 | ||||||||
| b 1 | -2 | -6 | ||||||||
| a 21 | -3 | -2 | -2 | -2 | -2 | -3 | -2 | -3 | ||
| a 22 | -2 | -3 | ||||||||
| b 2 | -6 | -6 | ||||||||
| a 31 | -1 | -1 | -2 | -2 | -1 | -1 | ||||
| a 32 | -2 | -4 | -2 | -3 | ||||||
| b 3 | ||||||||||
| a 41 | -1 | -1 | ||||||||
| a 42 | -1 | |||||||||
| b 4 | -2 | -2 | -2 | |||||||
| L(x) | min | min | max | min | max | max | max | min | max | max |
Задание 2. Фирма имеет три магазина розничной торговли, расположенных в разных районах города (А, В, С). Поставки продукции в эти магазины осуществляются с двух складов D и E, площади которых вмещают 30 и 25 т продукции, соответственно. В связи с возросшим покупательским спросом фирма планирует расширить площади магазинов, поэтому их потребности в продукции с торговых складов составят 20, 35 и 15 т в день. Чтобы удовлетворить спрос на продукцию, предполагается строительство третьего склада, площади которого позволят хранить в нем 15 т продукции ежедневно. Руководство фирмы рассматривает два варианта его размещения. В таблице даны транспортные издержки, соответствующие перевозке продукции с двух существующих складов и два варианта размещения нового склада.
Оценить две транспортные модели и принять решение, какой вариант размещения нового склада выгоднее.
| Торговый | Транспортные издержки, ден. ед. | ||
| Cклад | А | В | С |
| D | с 11 | с 12 | с 13 |
| E | с 21 | с 22 | с23 |
| Вариант 1 | с 31 | с 32 | с 33 |
| Вариант 2 | с 41 | с 42 | с 43 |
Значения коэффициентов
| N варианта | ||||||||||
| Значения | ||||||||||
| с 11 | ||||||||||
| с 12 | ||||||||||
| с 13 | ||||||||||
| с 21 | ||||||||||
| с 22 | ||||||||||
| с 23 | ||||||||||
| с 31 | ||||||||||
| с 32 | ||||||||||
| с 33 | ||||||||||
| с 41 | ||||||||||
| с 42 | ||||||||||
| с 43 |
Задание 3. Найти кратчайший путь от вершины 1 до любой другой вершины методом присвоения меток.
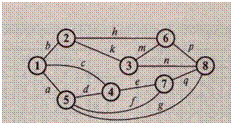
| Вар. | ||||||||||
| а | ||||||||||
| b | ||||||||||
| с | ||||||||||
| d | ||||||||||
| е | ||||||||||
| f | ||||||||||
| g | ||||||||||
| h | ||||||||||
| к | ||||||||||
| m | ||||||||||
| n | ||||||||||
| p | ||||||||||
| q | ||||||||||
| г | ||||||||||
| s | ||||||||||
| t | ||||||||||
| x | ||||||||||
| y | ||||||||||
| z | ||||||||||
| w |
Задание 4. Решить транспортную модель в сетевой постановке:
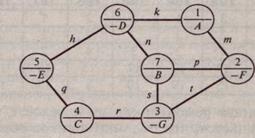
| Вариант | ||||||||||
| А | ||||||||||
| В | ||||||||||
| С | ||||||||||
| -D | -10 | -30 | -20 | -25 | -5 | -15 | -35 | -60 | -25 | -20 |
| -Е | -30 | -20 | -60 | -10 | -15 | -20 | -5 | -75 | -60 | -40 |
| -F | -25 | -60 | -40 | -20 | -30 | -25 | -30 | -35 | -15 | -25 |
| -G | -55 | -70 | -10 | -50 | -25 | -25 | -25 | -30 | -50 | -20 |
| h | ||||||||||
| k | ||||||||||
| m | ||||||||||
| n | ||||||||||
| p | ||||||||||
| q | ||||||||||
| г | ||||||||||
| s | ||||||||||
| t |
Задание 5. Для матрицы методом ветвей и границ решить задачу коммивояжера
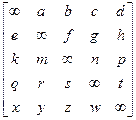
| Вар. | ||||||||||
| а | ||||||||||
| b | ||||||||||
| с | ||||||||||
| d | ||||||||||
| е | ||||||||||
| f | ||||||||||
| g | ||||||||||
| h | ||||||||||
| к | ||||||||||
| m | ||||||||||
| n | ||||||||||
| p | ||||||||||
| q | ||||||||||
| г | ||||||||||
| s | ||||||||||
| t | ||||||||||
| x | ||||||||||
| y | ||||||||||
| z | ||||||||||
| w |
|