
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторная работа № 1. Шифры замены
|
|
Сущность шифрования методом замены заключается в следующем. Пусть шифруются сообщения на русском языке и замене подлежит каждая буква этих сообщений.
Тогда, для буквы А исходного алфавита строится некоторое множество символов (шифрозамен) МА, для Б – МБ, …, для Я – МЯ.
Шифрозамены выбираютсятаким образом, чтобы любые два множества (МI и МJ, i ¹ j) не содержали одинаковых элементов (МI Ç МJ = Æ).
Таблица, приведенная на рис.2, является ключом шифра замены. Зная ее, можно осуществить как шифрование, так и расшифрование.
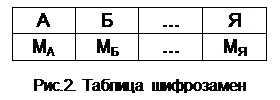 При шифровании каждая буква А открытого сообщения заменяется любым символом из множества МА.
При шифровании каждая буква А открытого сообщения заменяется любым символом из множества МА.
Если в сообщении содержится несколько букв А, то каждая из них заменяется на любой символ из МА. За счет этого с помощью одного ключа можно получить различные варианты шифрограммы для одного и того же открытого сообщения.
Так как множества МА, МБ,..., МЯ попарно не пересекаются, то по каждому символу шифрограммы можно однозначно определить, какому множеству он принадлежит.
Каждую букву открытого сообщения он заменяет. Поэтому расшифрование возможно и открытое сообщение определяется единственным образом.
Метод замены часто реализуется многими пользователями при работе на компьютере.
Если по забывчивости не переключить на клавиатуре набор символов с латиницы на кириллицу, то вместо букв русского алфавита при вводе текста будут печататься буквы латинского алфавита («шифрозамены»).
Шифры замены можно разделить на следующие подклассы:
- шифры однозначной замены (одноалфавитные). Количество шифрозамен для каждого символа исходного алфавита равно 1 (½ Мi ½ =1);
- шифры многозначной замены (многоалфавитные). Количество шифрозамен для отдельных символов исходного алфавита больше 1 (½ Мi ½ ≥ 1).
Для записи исходных и зашифрованных сообщений используются строго определенные алфавиты.
Под алфавитом в данном случае понимается набор символов, служащий для записи сообщений.
Алфавиты для записи исходных и зашифрованных сообщений могут отличаться.
Символы обоих алфавитов могут быть представлены буквами, их сочетаниями, числами, рисунками и т.п. В качестве примера можно привести пляшущих человечков из рассказа А. Конан Дойла ( ) и рукопись рунического письма (
) и рукопись рунического письма ( ) из романа Ж. Верна «Путешествие к центру Земли».
) из романа Ж. Верна «Путешествие к центру Земли».
Шифры однозначной замены. Максимальное количество ключей для любого шифра этой вида не превышает n!,
где n – количество символов в алфавите.
С увеличением числа n значение n! растет очень быстро (1! =1, 5! =120, 10! =3628800, 15! =1307674368000).
При больших n для приближенного вычисления n! можно воспользоваться формулой Стирлинга
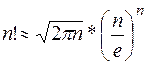 .
.
Шифр Цезаря (1 век до н.э.).
Данный шифр был придуман Гаем Юлием Цезарем и использовался им в своей переписке.
Применительно к русскому языку суть его состоит в следующем.
Выписывается исходный алфавит (А, Б,..., Я), затем под ним выписывается тот же алфавит, но с циклическим сдвигом на 3 буквы влево.
| А | Б | В | Г | Д | Е | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Ь | Ъ | Э | Ю | Я |
| Г | Д | Е | Е | Ж | И | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Ь | Ъ | Э | Ю | Я | А | Б | В |
Рис.3. Таблица шифрозамен для шифра Цезаря
При зашифровке буква А заменяется буквой Г, Б - на Д и т. д. Так, например, исходное сообщение «АБРАМОВ» после шифрования будет выглядеть «ГДУГПСЕ». Получатель сообщения «ГДУГПСЕ» ищет эти буквы в нижней строке и по буквам над ними восстанавливает исходное сообщение «АБРАМОВ».
Ключом в шифре Цезаря является величина сдвига нижней строки алфавита. Количество ключей для всех модификаций данного шифра применительно к алфавиту русского языка равна 33.
Лозунговый шифр.
Для данного шифра построение таблицы шифрозамен основано на лозунге (ключе) - легко запоминаемом слове. Вторая строка таблицы шифрозамен заполняется сначала словом-лозунгом (причем повторяющиеся буквы отбрасываются), а затем остальными буквами, не вошедшие в слово-лозунг, в алфавитном порядке. Например, если выбрано слово-лозунг «ДЯДИНА», то таблица имеет следующий вид.
| А | Б | В | Г | Д | Е | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Ь | Ъ | Э | Ю | Я |
| Д | Я | И | Н | А | Б | В | Г | Е | Е | Ж | З | Й | К | Л | М | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Ь | Ъ | Э | Ю |
Рис.4. Таблица шифрозамен для лозунгового шифра
При шифровании исходного сообщения «АБРАМОВ» по приведенному выше ключу шифрограмма будет выглядеть «ДЯПДКМИ».
 Полибианский квадрат.
Полибианский квадрат.
Шифр изобретен греческим писателем и историком Полибием. Прямоугольная таблица заполняется буквами алфавита в случайном порядке. Размер прямоугольника и порядок букв является ключом.
Каждая буква открытого сообщения заменяется буквой, расположенной ниже в том же столбце. Если буква находится на последней строке таблицы, то для ее шифрования берут самую верхнюю букву столбца. Например, если исходное сообщение «АБРАМОВ», то шифрограмма – «УФВУЭЬТ».
 Шифрующая система Трисемуса.
Шифрующая система Трисемуса.
Является сочетанием лозунгового шифра и полибианского квадрата.
В таблицу сначала вписывается ключевое слово, причем повторяющиеся буквы отбрасываются. Затем эта таблица дополняется не вошедшими в нее буквами алфавита.
На рис.6 изображена таблица с ключевым словом «ДЯДИНА».
Шифрование выполняется как и в предыдущем шифре (исходное сообщение «АБРАМОВ», зашифрованное – «ИЙЪИХШК»).
Одним из существенных недостатков шифров однозначной замены является их легкая вскрываемость.
При вскрытии шифрограмм используются различные приемы, которые даже при отсутствии мощных вычислительных средств позволяют добиться положительного результата. Один из таких приемов базируется на том, что в шифрограммах остается информация о частоте встречаемости букв исходного текста.
Если в открытом сообщении часто встречается какая-либо буква, то в шифрованном сообщении также часто будет встречаться соответствующий ей символ. Для разных языков мира существуют специальные таблицы с оценкой вероятности появления тех или иных букв в текстах.
Так, например, для русского языка такая таблица выглядит следующим образом.
Таблица 1
Вероятности появления букв русского языка в текстах*
| Буква (символ) | Вероят- ность | Буква | Вероят- ность | Буква | Вероят- Ность | Буква | Вероят- ность |
| Пробел | 0.146 | Р | 0.042 | Я | 0.017 | Ж | 0.007 |
| О | 0.094 | Л | 0.039 | З | 0.016 | Ш | 0.006 |
| Е | 0.071 | В | 0.038 | Ы | 0.015 | Ц, Ю | 0.005 |
| А | 0.069 | К | 0.029 | Г | 0.014 | Щ | 0.004 |
| И | 0.064 | М | 0.027 | Ь, Б | 0.013 | Ф | 0.003 |
| Н | 0.057 | П | 0.026 | Ч | 0.012 | Э | 0.002 |
| Т | 0.054 | Д | 0.024 | Й | 0.010 | Ъ | 0.001 |
| С | 0.046 | У | 0.023 | Х | 0.008 |
В таблице приведены оценки вероятностей появления букв русского языка и пробела, полученные на основе анализа научно-технических и художественных текстов общим объемом более 1000000 символов.
Существуют подобные таблицы для пар букв (биграмм). Например, часто встречаемыми биграммами являются «то», «но», «ст», «по», «ен» и т.д. Другой прием вскрытия шифрограмм основан на исключении возможных сочетаний букв. Например, в текстах (если они написаны без орфографических ошибок) нельзя встретить сочетаний «чя», «щы», «ьъ» и т.п.
Для усложнения задачи вскрытия шифров однозначной замены еще в древности перед шифрованием из исходных сообщений исключали пробелы и/или гласные буквы.
Шифры многозначной замены. Другое направление повышения стойкости шифров замены состоит в том, чтобы каждое множество шифробозначений Мi содержало более одного элемента. При использовании такого шифра одну и ту же букву (если она встречается несколько раз в исходном сообщении) заменяют на разные шифрозамены из Мi. Это позволяет скрыть истинную частоту букв открытого сообщения.