
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие температуры
|
|
Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Температура одинакова для всех частей изолированной системы, находящейся в термодинамическом равновесии. Если изолированная термодинамическая система не находится в равновесии, то с течением времени переход энергии (теплопередача) от более нагретых частей системы к менее нагретым приводит к выравниванию температуры во всей системе (нулевое начало термодинамики). В равновесных условиях температура пропорциональна средней кинетической энергии частиц тела.
Температура не может быть измерена непосредственно. Об изменении температуры судят по изменению других физических свойств тел (объёма, давления, электрического сопротивления, эдс, интенсивности излучения и др.), однозначно с ней связанных (так называемых термодинамических свойств). Любой метод измерения температуры связан с определением температурной шкалы.
Методы измерения температуры различны для различных диапазонов измеряемых температур, они зависят от условий измерений и требуемой точности. Их можно разделить на две основные группы: контактные и безконтактные. Для контактных методов характерно то, что прибор, измеряющий температуру среды, должен находиться в тепловом равновесии с ней, т.е. иметь с ней одинаковую температуру. Основными узлами всех приборов для измерения температуры являются чувствительный элемент, где реализуется термометрическое свойство, и измерительный прибор, связанный с элементом.
Согласно молекулярно–кинетической теории идеального газа температура есть величина, характеризующая среднюю кинетическую энергию поступательного движения молекул идеального газа. Учитывая термодинамический смысл температуры, можно свести измерение температуры любого тела к измерению средней кинетической энергии молекул идеального газа.
Однако на практике измеряют не энергию молекул по их скорости, а давление газа, которое находится в прямопропорциональной зависимости от энергии.
По молекулярно–кинетической теории идеального газа температура Т является мерой средней кинетической энергии поступательного движения молекул:
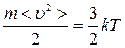 , (1)
, (1)
где 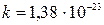 Дж/К – постоянная Больцмана;
Дж/К – постоянная Больцмана;
Т – абсолютная температура в кельвинах.
Основное уравнение молекулярно–кинетической теории идеального газа, устанавливающее зависимость давления 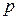 от кинетической энергии поступательного движения молекул газа, имеет вид:
от кинетической энергии поступательного движения молекул газа, имеет вид:
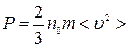 , (2)
, (2)
где 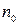 – число молекул в единице объёма, т.е. концентрация.
– число молекул в единице объёма, т.е. концентрация.
Используя уравнение (1) и (2), получаем зависимость
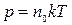 (3)
(3)
между давлением и температурой, которая позволяет установить, что давление идеального газа пропорционально его абсолютной температуре и концентрации молекул, где
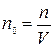 (4)
(4)
Измерение температуры основано на следующих двух опытных фактах:
а) если имеются два тела, каждое из которых находится в тепловом равновесии с одним и тем же третьем телом, то все три тела имеют одну и ту же температуру;
б) изменение температуры всегда сопровождается непрерывным изменением по меньшей мере одного из параметров, не считая самой температуры, характеризующего состояния тела, например: объём, давление, электропроводность и др. Первое из этих положений позволяет сравнивать температуры различных тел, не приводя их в соприкосновение между собой.
Второе положение позволяет выбрать один из параметров в качестве термометрического.
В общем случае температура определяется как производная от энергии в целом по его энтропии. Так определяемая температура всегда положительная (поскольку кинетическая энергия всегда положительная), её называют температурой или температурой по термодинамической шкале температур и обозначают Т. За единицу абсолютной температуры в системе СИ (Международная система единиц) принят кельвин (К). См. «Введение». Часто температуру измеряют по шкале Цельсия (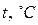 ), она связана с Т (К) равенством
), она связана с Т (К) равенством
 ;
; 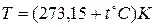 (5)
(5)
где 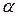 – термический коэффициент объёмного расширения газа.
– термический коэффициент объёмного расширения газа.
Уравнение Клапейрона–Менделеева и изопроцессы
Пусть некоторый газ переходит из состояния, определяемого параметрами 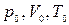 , в состоянии с
, в состоянии с 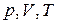 . Указанные параметры связаны равенством
. Указанные параметры связаны равенством
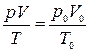 (6)
(6)
Это равенство называют уравнением состояния. Оно принимает простой вид, если массу газа выразить в молях.
Молем называют количество вещества, содержащее столько же структурных элементов, сколько содержится атомов в углероде 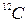 массой 0, 012кг.
массой 0, 012кг.
Моль любого вещества при нормальных условиях (давление 760 мм. рт. ст. и температура 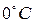 ) занимает одинаковый для всех газов объём – 22, 4 литра. Следовательно, для одного моля полученное уравнение (6) имеет вид:
) занимает одинаковый для всех газов объём – 22, 4 литра. Следовательно, для одного моля полученное уравнение (6) имеет вид:
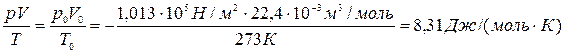
Полученную постоянную величину обозначают буквой R
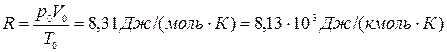
и называют молярной газовой постоянной.
Очевидно, что для 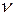 молей газа получим
молей газа получим
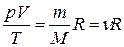 или
или 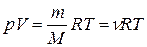 , (7)
, (7)
где т – масса газа;
М – молярная масса данного газа;
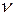 – число молей газа.
– число молей газа.
Это уравнение называют уравнением Клапейрона–Менделеева.
Процессы в газах, протекающие при неизменности какого–либо параметра, называют изопроцессами.
Процесс, протекающий при неизменной температуре, называется изотермическим. Уравнение изотермического процесса (закон Бойля–Мариотта) записывается так:
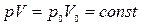 , (8)
, (8)
где 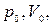
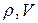 – давление объём данной массы газа в начальной и конечном состояниях.
– давление объём данной массы газа в начальной и конечном состояниях.
Процесс, протекающий при неизменном давлении, называется изобарическим. Уравнение изобарического процесса (закон Гей–Люссака) может быть представлен в виде:
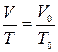 или
или 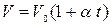 , (9)
, (9)
где 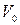 – объём газа при
– объём газа при 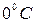 ;
;
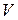 – объём того же газа при температуре Т;
– объём того же газа при температуре Т;
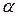 – термический коэффициент объёмного расширения газа, одинаковый для всех газов:
– термический коэффициент объёмного расширения газа, одинаковый для всех газов: 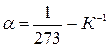 .
.
Величину 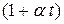 называют биномом объёмного расширения.
называют биномом объёмного расширения.
Процесс, протекающий при неизменном объёме, называется изохорическим. Уравнение изохорического процесса называют уравнением Шарля
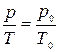 или
или 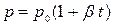 (10)
(10)
где 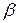 – термический коэффициент давления.
– термический коэффициент давления.
Для идеальных газов, т.е. газов, точно подчиняющихся законам Бойля–Мариотта и Гей–Люссака,
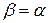 (11)
(11)
На рис. 1 показаны графики изопроцессов в координатах 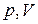 .
.
