
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
минимума.
|
|
КАЛУЖСКИЙ ФИЛИАЛ
Факультет Агрономический
Кафедра «Механизации сельскохозяйственного производства»
О Т Ч Е Т
ДОМАШНЕЕ ЗАДАНИЕ №2
| ДИСЦИПЛИНА: | " Метрология, стандартизация и сертификация" |
Выполнил: студент гр. А-32 Суворкин В.А._________________
Проверил доцент: Чубаров Ф. Л. ________________
Калуга 2015
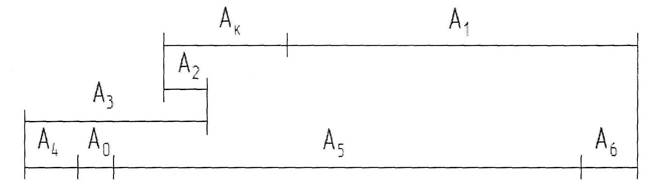
№14, сx. 1
Часть I. Расчет сборочной размерной цепи при обеспечении точности замыкающего звена методом регулирования.
Дано: А0=1..0.4; А, = 126Н11; А2 = 8Н12; А3 = 18Н12; А4 = 7Ы2; A5=126h9; A6=5hl2.
1)
2)
| Звено | Характер звена | Ном. размер, мм. | Услов.об-озн. поля допуска | Допуск, мкм. | Отклонения, мкм | Предельные размеры, мм. | |||
| Es(Aj) | Ei(Aj) | Ec(Aj) | Aj min | Aj max | |||||
| Ao | замык. | — | + 1000 | +400 | +700 | 0.4 | i | ||
| A1 | ув. | Н11 | +250 | + 125 | 126, 25 | ||||
| A2 | ум. | H12 | + 150 | +75 | 8, 15 | ||||
| A3 | ув. | Н12 | + 180 | ' +90 | 18, 18 | ||||
| A4 | ум. | h 2 | -150 | -75 | 6, 85 | ||||
| A5 | ум. | h9 | -100 | -50 | 125, 9 | ||||
| A6 | ум. | h12 | -120 | -60 | 4, 88 |
3) Определим номинальный размер компенсирующего звена:
n
Ао=∑ (Aj)yв. - (Aj) ум. ± Uk • Ak;
j = 1
где Uk =+1, т.к. Ak - увеличивающее звено
0 = (126+18) - (8+7+126+5) + Аk
0 = 144 - 146 + Ак, следовательно Ак = 2 (мм);
4) Определим диапазон компенсирования:
Т-2
ТА0= ∑ T Aj - Vk, где n + р = m - 2
600 = (250+150+180+150+100+120) -Vk Vk= 950-600 = 350 (мкм);
5) Определяем предельные отклонения Аk;
|
j=1 j=1
+700 = (+125+90) - (+75-75-50-60) + Ec(Ak);
Ec(Ak)= +700-325= +375 (мкм);
Es(Ak) = Ec(Ak) + Vk/2 = +375 + 350/2 = +550 (мкм); Ei(Ak) = Ec(Ak) - Vk/2 = +375 - 350/2 = +200 (мкм);
6) Определим предельные размеры Ак:
Ак mах = Ак ном + Es(Ak) = 2 + 0.55 = 2, 55 (мм);
Ак min = Ак ном + Ei(Ak) = 2 + 0.2 = 2, 2 (мм);
7) Определим толщину постоянной прокладки:
Sпост ≤ Aк min => S пост = 2≤ A к min =2, 2
Подсчитаем минимальное необходимое количество сменных прокладок:
N = [ Vk / ТА0 ] = [ 350/600 ] = 1;
Определим толщину сменных прокладок: S = Vk/ N = 350/1 = 350 (мкм) = =0.350(мм) => S = 0.6 мм
• S ≤ TA0=> 0.6 = 0.6;
• Sпост+ N•S ≤ Akmax => 2 + 1 • 0.6 = 2, 6 < 2, 55
Проверка:
N p
a) A0 max =∑ (AJ) УВmах - ∑ (A-0 УМ min + A k min;
j=1 j=1
n р
б) А0 min = ∑ (Аj) УВmin - ∑ (Aj) УМmах + Аk mах;
j=1 j=1
а) 1 =(126, 25+18, 18) - (8+6, 85+125, 9+4, 88)+ 2, 2=1 (мм);
б) 0, 4 = (126+18) - (8, 15+7+126+5) + 2, 55 = 0, 4 (мм);
n р
в) Es(A0) = ∑ Es(Аj) УВ - ∑ Ei(Aj) УМ + Ei (Аk);
j=1 j=1
n р
г) Ei(A0) = ∑ Ei(Аj) УВ - ∑ Es(Aj) УМ + Es (Аk);
j=1 j=1
в) +1000 = (+250+180) - (0 - 150 - 100 - 120) + 200 = +1000 (мкм);
г) +400 = 0 - (+150) + 550 = +400 (мкм).
Полученные тождества показывают, что расчеты произведены правильно.
Часть 2. Расчет подетальной размерной цепи методом максимума-
минимума.
Дано: 1) Номинальные размеры составляющих звеньев: B1=216; В2=61; В3=27;
В4=34; В5=65; В6=29.
2) Последовательность обработки: В1В2В3В6В5.
3) В3+В4+В5 = А5, А5 = 126h9 = 126
- 0, 1
1) Построим размерную цепь:
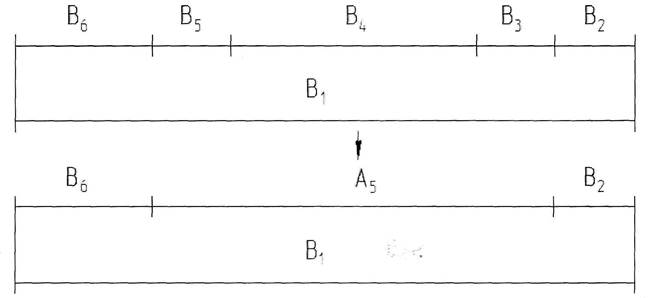
2) Определим аср аср=ТА5/∑ ij;
аср= 100/(2, 9+1, 86+1, 31) = 16, 5
Назначим допуски на составляющие звенья по 7 квалитету, взяв в качестве
т-2
резервного звена В1 => ТВ2 = 30, ТВ6 = 21 => ТВрез = ТВ1 = ТА5 - ∑ TBj = 100 -
j=1
-(30+21) = 49 (мкм);
3) Назначим предельные отклонения звеньев В2, В6, так, чтобы поля допусков располагались по ходу обработки:
для В2 → Es(B2) = +30 и Ei(B2) - 0 (мкм); для В6→ Es(B6) = +21 и Ei(B6) = 0 (мкм);
+0, 03 +0, 021
В2=61, В6 = 29.
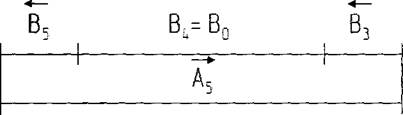
4) Определим предельные отклонения замыкающего звена:
|
В4=В0= 34 (мм); В3=27 + 0, 021; В5= 65+0, 03; А5 = 81126
-0, 1
а) Es(B0) = ∑ Es(Bj)yв. - ∑ Ei(Bj)yм. => Es (B0) = 0 - (0+0) = 0 (мкм);
б) Ei(B0) = ∑ Ei(Bj)yв. - ∑ Es(Bj)yм. => Ei (B0) = -100- (21+30) = -151 (мкм);
В0 = 34
-0, 151
5) Определим нестандартный допуск и предельные отклонения резервного звена:
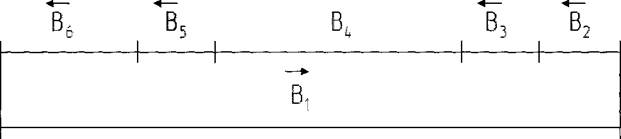
а) Es(B0) = ∑ Es(Bj)yв. - ∑ Ei(Bj,)yм. =>
=> Es (ВРез) = 0 + 0 = 0 (мкм);
б) Ei(B0)= ∑ Ei(Bj)yв.- ∑ Es(Bj)yм. =>
=> Ei (Врез) = - 151 + (30+21+30+21) = - 49 (мкм);
В рез= В1=216
-0.049
Проверка:
Ес(В0) = ∑ Ec(Bj)yв. -∑ Ес(Вj)ум.; Ec(Bj) = Es(Bj) - TBj/2 =>
Ec(B0) = Es(B0) - TB0/2= 0 - 151/2 = - 75, 5 (мкм);
Ec(B2) = Es(B2) - TB2/2 = 30 - 30/2 = 15 (мкм);
Ec(B3) = Es(B3) - TB3/2 = 21 - 21/2 = 10, 5 (мкм);
Ec(B5) = Es(B5) - TB5/2 = 30 - 30/2 = 15 (мкм);
Ec(B6) = Es(B6) -TB6/2 = 21 - 21/2 = 10, 5 (мкм); =>
Ec(Bpeз) = Es(Bpeз) - ТВрез/2 = 0 - 49/2 = - 24, 5 (мкм);
Ec(B1) = Ес(Врез) = - 24, 5 (мкм);
Es(Bpeз) = Es(B1) = Ec(B1) + ТВ1/2
0 = - 24, 5 + 49/2 = 0;
Ei(Bpeз) = Ei(B1) = Ec(B1)-TB1/2
- 49 = - 24, 5 - 49/2 = -49 => Расчеты верны.
|