
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерии оценки прогнозных результатов
|
|
ВЕРИФИКАЦИЯ ПРОГНОЗОВ
И ОЦЕНКА КАЧЕСТВА ПЛАНОВ
Критерии оценки прогнозных результатов
Показатели, используемые для анализа качества прогноза разделить на три группы:
1. Абсолютные показатели точности прогнозов. К ним относятся такие показатели, которые позволяют количественно определить величину ошибки прогноза в единицах измерения прогнозируемого объекта или в процентах:
- абсолютная ошибка:
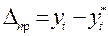 . (17.1)
. (17.1)
- средняя абсолютная ошибка:
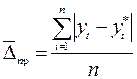 . (17.2)
. (17.2)
- среднеквадратическая ошибка:
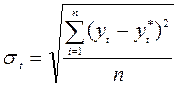 . (17.3)
. (17.3)
Следует отметить, что существует связь среднего абсолютного отклонения со стандартным отклонением. Для большого класса статистических распределений значение стандартного отклонения несколько больше значения среднего абсолютного отклонения и строго пропорционально ему. Константа пропорциональности для различных распределений колеблется между 1, 2 и 1, 3. Чаще всего на практике берется 1, 25, поэтому:
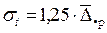 . (17.4)
. (17.4)
Недостатком рассматриваемых показателей является то, что значение этих характеристик существенного зависит от масштаба измерения уровней исследуемых явлений.
Абсолютная ошибка может быть выражена в процентах относительно фактических значений показателя следующим образом.
- относительная ошибка:
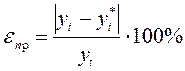 . (17.5)
. (17.5)
- средняя относительная ошибка:
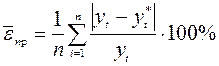 . (17.6)
. (17.6)
Данный показатель используется при сравнении точности прогнозов разнородных объектов прогнозирования, поскольку этот показатель характеризует относительную точность прогноза. Типичные значения показателя для среднесрочных прогнозов и их интерпретация представлены в таблице 17.1
Таблица 17.1 - Типичные значения показателя для среднесрочных прогнозов
| Средняя относительная ошибка, % | Интерпретация |
| < 10 | высокая точность |
| 10-20 | хорошая точность |
| 20-50 | удовлетворительная точность |
| > 50 | неудовлетворительная точность |
Подобный подход к оценке точности прогноза возможен только при условии, когда период упреждения уже окончился и имеются фактические данные о прогнозируемом показателе, а также при ретроспективном прогнозировании. В последнем случае имеющаяся информация делится на две части, одна из которых охватывает более ранние данные, а другая - более поздние. С помощью данных первой группы оцениваются параметры модели прогноза, а данные второй группы рассматриваются как фактические данные прогнозируемого показателя. Полученная ретроспективно ошибка прогноза в какой-то мере характеризует точность применяемой методики прогнозирования.
2. Сравнительные показатели точности прогнозов. Эти показатели основаны на сравнении ошибки рассматриваемого прогноза с эталонными прогнозами определенного вида. Один из таких показателей (К) может быть в общем виде представлен следующим образом:
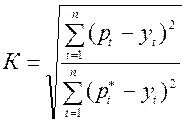 , (17.7)
, (17.7)
где рt* - прогнозируемое значение величины эталонного прогноза.
В качестве эталонного прогноза может быть выбрана простая экстраполяция, постоянный темп прироста и т.д. Частным случаем показателей такого типа является коэффициент несоответствия (КН), в котором pt*=0 для всех t:
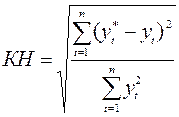 . (17.8)
. (17.8)
КН=0 в случае несовершенного прогноза и КН=1, когда прогноз имеет ту же ошибку, что и наивная экстраполяция неизменности. КН не имеет верхней конечной границы. Можно построить различные модификации коэффициента несоответствия:
- коэффициент несоответствия КН1, исчисляемый как отношение среднеквадратической ошибки прогноза к той же ошибке, которая имела бы место, если принять в качестве прогноза для каждого года среднее значение переменной за весь период:
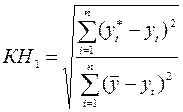 . (17.9)
. (17.9)
Если КН1> 1, то прогноз на уровне среднего значения дал бы лучшие результаты, чем имеющийся прогноз.
- коэффициент расхождения V, исчисляемый как отношение среднеквадратической ошибки прогноза к той же ошибке, которая имела бы место, если принять в качестве прогноза для каждого года экстраполированное значение по аналитическому тренду, то есть
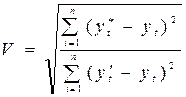 . (17.10)
. (17.10)
Если V> 1, то прогноз методом простой экстраполяции дает лучший результат.
К сравнительным показателям следует отнести и коэффициент корреляции между прогнозируемыми т фактическими значениями переменной - R.