Потенциальное движение жидкости

10.1.1 Общие сведения

Условие безвихревого движения (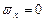, , 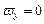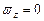) можно получить из уравнений (8.10):

, (10.1)

Формулы (10.1) выражают условие отсутствия вращательного движения жидкой частицы. С математической точки зрения, равенства (10.1) выражают тот факт, что существует некоторая функция координат 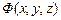, частные производные от которой по координатам равны проекциям скорости на соответствующие оси координат, т. е.

. (10.2)

Функция 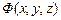называется потенциалом скорости. Понятие потенциала скорости в аэрогидрамеханике тождественно понятию потенциала сил в механике твердого тела. Из механики известно, что производная потенциала сил по какому-либо направлению дает проекцию потенциальной силы, действующей в этом направлении. По аналогии интенсивность изменения потенциала скорости в направлении координатных осей определяет проекции скорости на соответствующие оси [формулы (10.2)].

Таким образом потенциальное движение газа в изолированной системе является изоэнтропическим, т. е. если поток безвихревой и адиабатический, то изменение энтропии по любому направлению в потоке равно нулю и течение газа - описывается некоторой функцией координат .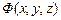

10.1.2 Вывод уравнения потенциала скоростей

Будем рассматривать только плоские потенциальные течения газа. Для плоского установившегося потока в предположени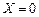и и уравнения (8.22) и (8.27) дают:

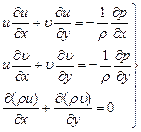(10.3)

Градиенты давления 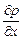и можно выразить следующим образом:

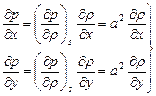. (10.4)

Из третьего уравнения (10.3) после дифференцирования получаем:

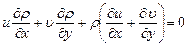. (10.5)

После подстановки (10.4) в (10.3) будем иметь:

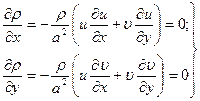. (10.6)

Подставляя производные плотности в (10.5), получаем:

. (10.7)

Имея в виду (10.2), перепишем (10.7) в виде:

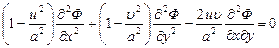. (10.8)

Уравнение (10.7) является нелинейным дифференциальным уравнением потенциала скоростей в частных производных второго порядка.

10.1.3 Применение потенциала

Введение потенциала скорости позволило систему трех уравнений (10.3) свести к одному (10.7), уменьшить число неизвестных с шести до пяти и оставить в уравнении только кинематические параметры.

Если в исследуемом поле потока известен потенциал скорости 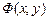, то при заданных граничных условиях могут быть определены все параметры течения. Потенциал скорости позволяет определить скорости потока 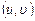по формулам (10.2). С помощью уравнения энергии совместно с уравнением изоэнтропического процесса легко определяются давление 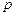, плотность и температура газа .

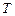Таким образом, при исследовании потенциальных движений газа основная задача сводится к определению потенциала скоростей 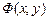для данного вида движения, т. е. к нахождению решения уравнения (10.7). Если потенциальная функция 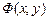определена, то кинематическая часть задачи решена. Далее без особых затруднений решается и динамическая часть задачи. Однако уравнение (10.7) в общем виде не интегрируется.

Потенциальная функция должна удовлетворять определенным начальным и граничным условиям данной конкретной задачи. В качестве кинематических начальных условий должно быть задано распределение параметров течения в определенной (начальной) области потока, а также должны быть известны условия на границе обтекаемого тела. При решении конкретных задач обтекания тел чаще всего задаются параметры течения невозмущенного потока на бесконечном удалении от тела (начальные условия) и условия непротекаемости - нормальная составляющая скорость у поверхности тела равна нулю (граничные условия).

Так, например, если плоский поток в бесконечности параллелен оси 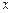, то потенциал скорости должен отвечать следующим условиям:

;

.

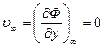При этом известными должны быть остальные параметры: , 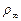и 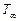.