Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение.
|
|
| Группы работников по выработке изделий за смену, шт. | Число работников, чел. (f) | Середина интервалов (x) | x*f |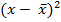 
| 
|
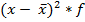
| до 30 | (-19)2=361 | ||||
| 30-40 | (-9)2=81 | ||||
| 40-50 | 12=1 | ||||
| 50-60 | 112=121 | ||||
| 60 и более | 212=441 | ||||
| Итого |
1) Найдем среднюю выработку изделий за смену по формуле средней арифметической взвешенной
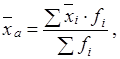
где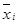 
- середина интервала;
fi. – число работников в каждом интервале.
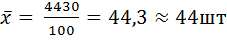- средняя выработка одного рабочего
2) Дисперсию признака определим по формуле:
.
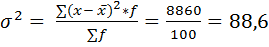(дисперсия)
Среднее квадратическое отклонение:
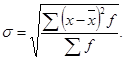
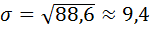(среднее квадратичное отклонение)
3) Коэффициент вариации (V) вычисляется процентным отношением среднего квадратического отклонения к средней арифметической:
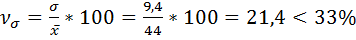- совокупность количественно однородная
4) По условию задачи было произведено 10%-ное выборочное обследование (по методу механического отбора). Поэтому численность генеральной совокупности N = 1000 чел.
Определим удельный вес работников предприятия, производящих более 50 изделий:
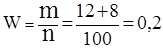или 20 %.
При заданной вероятности P = 0, 954 коэффициент доверия t = 2. Вычислим предельную ошибку выборки для генеральной доли:
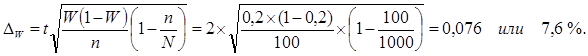
Определим пределы удельного веса работников предприятия, производящих более 50 изделий:
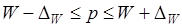
0, 2 – 0, 076 £ р£ 0, 2 + 0, 076,
0, 124 £ р£ 0, 276 или 12, 4 % £ р £ 27, 6 %.
Вывод: с вероятностью 0, 954 можно гарантировать, что в генеральной совокупности (N = 1000 чел.) доля работников предприятия, производящих более 50 изделий будет находиться в пределах от 12, 4 до 27, 6 %.