Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Что понимается под сходимостью итерационного процесса?
|
|
Ответ: К прямым относятся методы, позволяющие получить решение в результате конечного числа арифметических операций, зависящего только от вычислительной схемы, а также от порядка и структуры матрицы коэффициентов системы уравнений. В математике методы этой
группы называются также точными, поскольку если исходные данные заданы точно и вычисления выполняются точно, то решение также получается точным. К итерационным относятся методы, с помощью которых решение системы линейных алгебраических уравнений получается как предел
последовательных приближений, вычисляемых посредством единообразных операций. В математике итерационные методы называются приближенными, поскольку даже в предположении, что вычисления ведутся без округлений, они позволяют получить решение системы уравнений лишь с заданной точностью. Практически в основе всех прямых методов решения линейных алгебраических уравнений установившегося режима электрической системы лежит метод последовательного исключения неизвестных, называемый методом Гаусса. К числу наиболее характерных вычислительных схем этого метода относятся алгоритмы с обратным ходом и без обратного хода. Решение системы из n линейных алгебраических уравнений вида 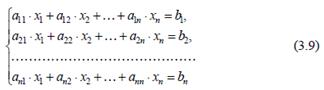 по этому алгоритму состоит из двух этапов: 1)на 1-м этапе (прямой ход) исходная система за n однотипных шагов преобразуется таким образом, что матрица коэффициентов преобразованной системы становится верхней треугольной, т. е. все элементы, расположенные ниже ее главной диагонали, равны нулю; 2)на 2-м этапе (обратный ход) последовательно определяются значения неизвестных от хn до х1.
по этому алгоритму состоит из двух этапов: 1)на 1-м этапе (прямой ход) исходная система за n однотипных шагов преобразуется таким образом, что матрица коэффициентов преобразованной системы становится верхней треугольной, т. е. все элементы, расположенные ниже ее главной диагонали, равны нулю; 2)на 2-м этапе (обратный ход) последовательно определяются значения неизвестных от хn до х1.




Метод Гаусса прост, нагляден и легко программируется на ЭВМ. Однако его применение не всегда позволяет получить решение с приемлемой точностью либо не позволяет получить его вообще. К причинам возникновения недопустимо большой погрешности относятся округление результатов вычислений и неточность исходных данных (что характерно для инженерных задач), которая в ряде случаев может вызвать несоразмерно большое снижение точности. Итерационные методы решениясистем линейных алгебраических уравнений позволяют получить значения искомых неизвестных в результате многократного выполнения единообразных шагов вычислений, называемых последовательными приближениями, или итерациями. В отличие от прямых методов, решение можно получить только с заданной точностью, причем с увеличением точности растет и число итераций. 
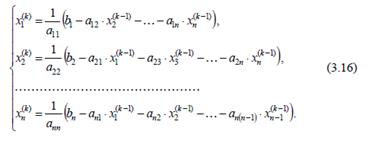


На рис. 3.2 показан характер изменения итерационной переменной х в зависимости от номера итерации N для случаев сходящегося и расходящегося итерационного процесса.