Тесты FEPO по математическому анализу

1. Предел 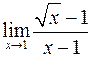равен

1; 0; ;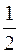

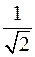
2. Точка разрыва функции

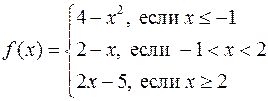
Равна: 2; 0; -1; 3

3. Горизонтальная асимптота функции 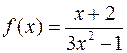задается уравнением вида:

, , ,

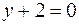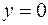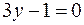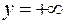
4. Производная функции 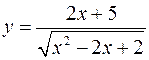равна

; ; ;

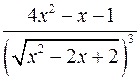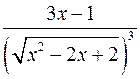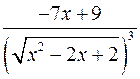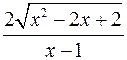
5. Производная третьего порядка функции 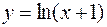равна

; ; ;

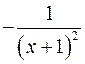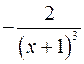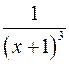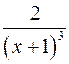
6. Минимум функции 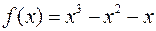равен

-3; 1; -1;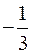

7. Множество первообразных функции 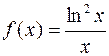имеет вид

; ; ;

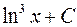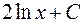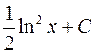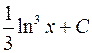
8. Определенный интеграл 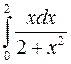равен

; ; ;

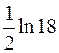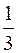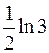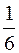
9. Площадь фигуры, изображенной на рисунке равна

; ; ;

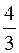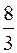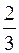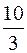
10. Производная функции 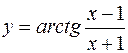равна

; ; ; .

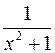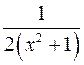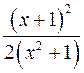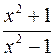11. Определенный интеграл 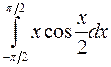равен

1; 0; ;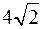

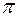
12. Область определения функции имеет вид

; ; ;

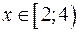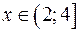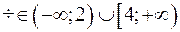
13. Предел 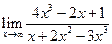равен 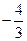; 1; 4; .

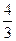14. Функция 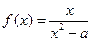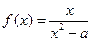не прерывается на отрезке ; ; ; .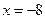

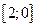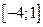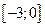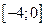15. Вертикальная ассимтота равна функции 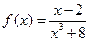называется уравнением в виде

16. ; ; ;

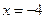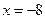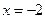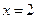
17. Производная второго порядка функции 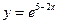равна

; ; ; .

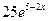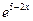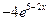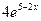18. Определенный интеграл 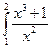равен 1; 2; ; .

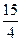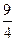19. Площадь фигуры на рисунке равна

20. Производная функции 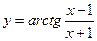равна ; ; ;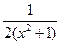

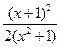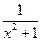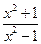
21. Если функция 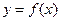прерывается на отрезке , то 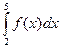можно представить в виде ; ; .

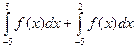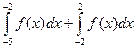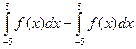22. Ассимптотой функции 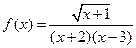называется уравнение в виде x=3; x=0; x= -2; x= -1

23. Производная функции 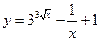равна

; ; ; .

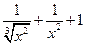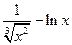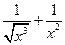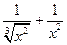24. Производная второго порядка функции 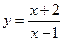равна ; ;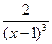

; .

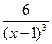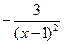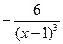25. Наибольшее значение функции 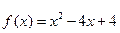на отрезке 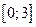равно

16; 4; 2; 1.

26. Множество первообразных 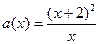имеет вид

;

; ; .

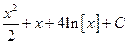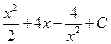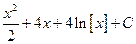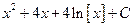27. Определенный интеграл 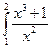равен 2; 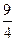; 1;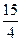