Краткая теория. Цель работы: Измерить период для различных осей вращения, Определить ускорение свободного падения g.

Лабораторная работа №20

ОБОРОТНЫЙ МАЯТНИК

Цель работы: Измерить период для различных осей вращения, Определить ускорение свободного падения g.

Приборы и принадлежности

Оборотный маятник, рулетка, секундомер.

Краткая теория

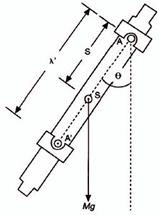
Физический маятник (рис. 2) отличается от математического тем, что его колеблющаяся масса находится не в одной точке, а распределяется в пространстве.

Потенциальная энергия маятника 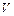возникает из потенциальной энергии центра тяжести :

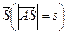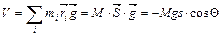, (1)

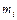где и 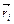- масса и координат 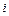-й частицы по отношению к оси вращения 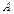; 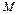- общая масса маятника, а 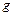- ускорение свободного падения.

Кинетическая энергия 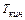физического маятника равна сумме кинетических энергий его частиц:

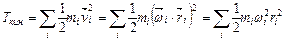, (2)

где 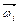- угловая скорость 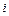-й частицы 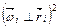, которая (в случае с твердым телом) равна 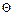для всех частиц маятника.

Рис. 2: Оборотный маятник.

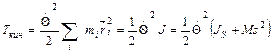(3)

Момент инерции 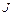относительно оси вращения 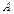заменим на момент инерции маятника 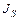относительно параллельной линии, проходящей через центр гравитации 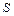оси (Закон Штейнера).

Учитывая закон сохранения энергии в системе, получаем:

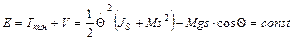
Это дифференциальное уравнение первого порядка, имеющее аналитические решения для малых колебаний (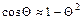; 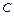- const):

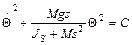(4)

Общее решение уравнения (4) имеет вид:

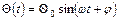, (5)

где 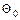- амплитуда колебания, 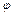- фаза, а частота колебания выражается как:

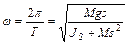(6)

Определяем уменьшенную длину маятника :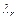

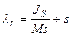, (7)

а период 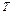простого физического маятника как:

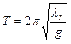(8)

Таким образом, период 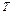у физического маятника такой же, как и у математического (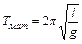) с длиной 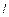= 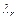. С одной стороны период физического маятника зависит от массы маятника, в отличие от математического, с другой стороны, уменьшенная длина 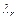маятника всегда больше расстояния 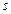между центром тяжести и осью вращения, поэтому скорость колебания маятника увеличивается, если масса сконцентрирована возле центра гравитации.

Точка 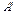, расположенная на продолжении луча 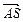на расстоянии 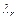относительно оси вращения 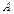(рис. 2), является центром колебаний. Если ось вращения маятника сместить от 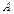до 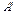, период колебания физического маятника остается неизменным, т.к. из выражений (7) и (8) и нового расстояния оси вращения из центра тяжести 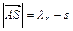следует, что:

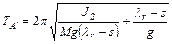
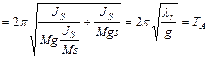
Таким образом, физический маятник для любой оси вращения 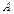имеет центр колебаний в точке 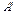; если обе точки являются осями вращения 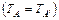, период остается низменным. Кроме этого, в данном эксперименте периоды одинаковы в случае симметрии (оборотные оси равноудалены от центра тяжести 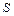); т.е. 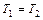(ср. рис. 3). Из рис. 3 видно, что с одной стороны вблизи центра тяжести период стремится к бесконечности, а с другой, что существует ось вращения (для 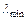), для которой период минимален.

На рис. 3 изменение момента инерции и сдвиг центра тяжести из-за перемещения опорных втулок по штативному стержню не учитывались (однако, основная картина не изменилась). Эта погрешность обнаруживается при контрольном измерении периода 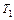вокруг оси вращения 1, значение которой 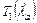заметно отличается от значения, полученного для симметричного случая .

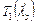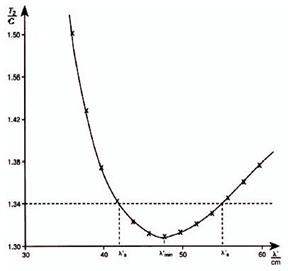
Рис. 3: Зависимость периода колебаний от положения оси вращения физического маятника.

Рис. 4: Определение уменьшенной длины маятника