
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания 4 страница
|
|
Выполним обратное преобразование Лапласа с помощью теоремы разложения. Обозначим числитель и знаменатель дроби (3.19) соответственно 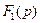 и
и 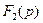 :
:
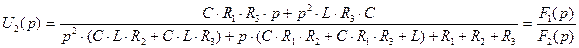
(3.20)
Приравниваем знаменатель выражения (3.20) к нулю - 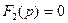 и находим корни заданного квадратного уравнения:
и находим корни заданного квадратного уравнения:
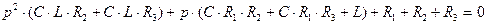 (3.21)
(3.21)
Корни заданного уравнения будут совпадать с корнями при расчете переходной характеристики, так как заданные уравнения идентичны:
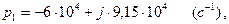 (3.22)
(3.22)
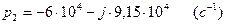 (3.23)
(3.23)
Найдем производную от знаменателя дроби (3.20) то есть 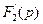 :
:
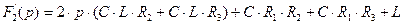 (3.24)
(3.24)
В соответствии с теоремой разложения 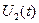 имеет вид:
имеет вид:
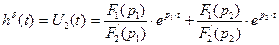 (3.25)
(3.25)
Найдём, 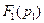 подставив вместо
подставив вместо 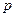 в выражении (числитель) (3.20) первый корень характеристического уравнения (3.22):
в выражении (числитель) (3.20) первый корень характеристического уравнения (3.22):
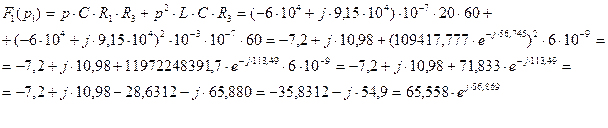
(3.26)
Найдём, 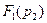 подставив вместо
подставив вместо 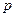 в выражении (числитель) (3.20) второй корень характеристического уравнения (3.23):
в выражении (числитель) (3.20) второй корень характеристического уравнения (3.23):

(3.27)
В выражение (3.24) подставим первый корень характеристического уравнения (3.22) и получим:
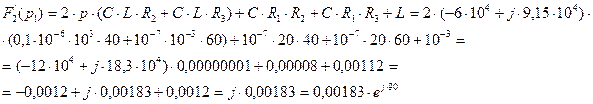
(3.28)
В выражение (3.24) подставим второй корень характеристического уравнения (3.23) и получим:
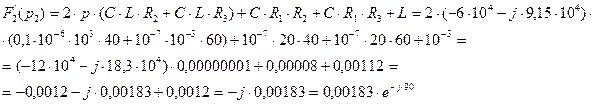
(3.29)
Подставляем найденные значения (3.26), (3.27), (3.28) и (3.29) в выражение (3.25):
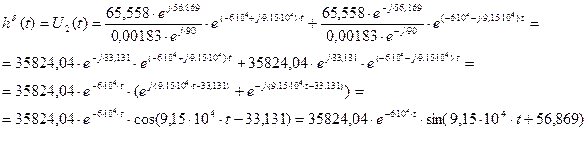
(3.30)
Получили выражение, представляющее собой импульсную характеристику заданного четырехполюсника (3.30).
Графики переходной и импульсной характеристик, в случае, когда корни характеристического уравнения комплексно – сопряженные, приведены в Приложении В.
Данные расчёта переходной и импульсной характеристик, в случае, когда корни характеристического уравнения комплексно - сопряженные приведены в таблице 3.2.
Таблица 3.2 - Данные расчёта переходной и импульсной характеристик, в случае, когда корни характеристического уравнения комплексно – сопряженные.

| 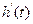
| 
|
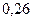
| 
| |
| 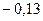
| 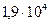
|
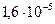
| 
| 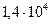
|
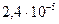
| 
| 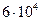
|
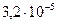
| 
| 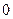
|
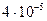
| 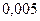
| 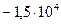
|
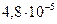
| 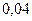
| 
|
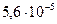
| 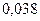
| 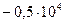
|
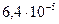
| 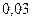
| 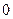
|
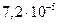
| 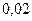
| 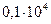
|
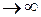
| 0 |
4 Расчет 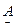 - параметров четырехполюсника
- параметров четырехполюсника
При записи уравнений в форме 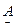 положительное направление токов выбирается согласно рисунку 4.1. Удобство выбора именно такого положительного направления тока
положительное направление токов выбирается согласно рисунку 4.1. Удобство выбора именно такого положительного направления тока 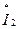 связано в данном случае с тем, что форма
связано в данном случае с тем, что форма 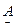 применяется обычно при передаче электрической энергии от входных выводов к выходным, причем четырехполюсник, включенный между источником и приёмником, может состоять из нескольких четырехполюсников, соединенных каскадно; вход каждого последующего четырехполюсника совпадает с выходом предыдущего четырехполюсника.
применяется обычно при передаче электрической энергии от входных выводов к выходным, причем четырехполюсник, включенный между источником и приёмником, может состоять из нескольких четырехполюсников, соединенных каскадно; вход каждого последующего четырехполюсника совпадает с выходом предыдущего четырехполюсника.
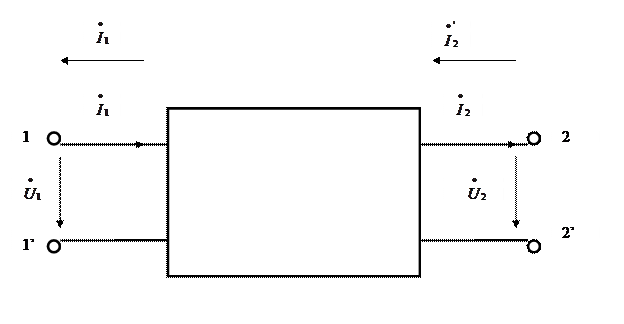
Рисунок 4.1 – Положительное направление токов и напряжений четырехполюсника
Вариант с токами 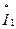 и
и 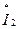 называется прямой передачей, вариант с токами
называется прямой передачей, вариант с токами 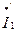 и
и 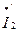 называется обратной передачей.
называется обратной передачей.
Коэффициенты 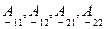 в общем случае комплексные и зависят от частоты:
в общем случае комплексные и зависят от частоты: 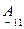 и
и 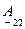 - безразмерные,
- безразмерные,  - имеет размерность сопротивлений,
- имеет размерность сопротивлений, 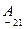 имеет размерность проводимости. Эти коэффициенты могут быть определены следующим образом (рисунок 4.1):
имеет размерность проводимости. Эти коэффициенты могут быть определены следующим образом (рисунок 4.1):
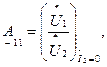 - отношение напряжений при разомкнутых выходных зажимах;
- отношение напряжений при разомкнутых выходных зажимах;
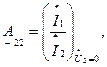 - отношение токов при закороченных выходных зажимах;
- отношение токов при закороченных выходных зажимах;
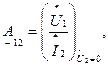 - величина, обратная передаточной проводимости при закороченных выходных зажимах;
- величина, обратная передаточной проводимости при закороченных выходных зажимах;
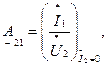 - величина, обратная передаточному сопротивлению при разомкнутых выходных зажимах;
- величина, обратная передаточному сопротивлению при разомкнутых выходных зажимах;
В нашем случае расчет 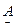 - параметров будет произведен через параметры холостого хода и короткого замыкания.
- параметров будет произведен через параметры холостого хода и короткого замыкания.
Коэффициенты  и
и 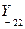 представляют собой входные проводимости четырехполюсника рисунок 4.1, измеренные слева и справа при закороченных противоположных выводах; соответственно
представляют собой входные проводимости четырехполюсника рисунок 4.1, измеренные слева и справа при закороченных противоположных выводах; соответственно 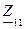 и
и  представляют собой
представляют собой
входные сопротивления четырехполюсника при разомкнутых выводах.
Введя индексы «к» и «х» для обозначения режимов короткого замыкания (выводы замкнуты) и холостого хода (выводы разомкнуты), получим параметры холостого хода и короткого замыкания:
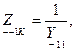
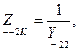
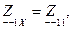
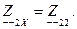
Параметры холостого хода и короткого замыкания могут быть выражены через любую систему коэффициентов, например через коэффициенты 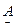 :
:
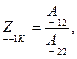
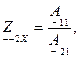
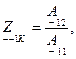
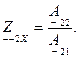
В свою очередь любая система коэффициентов обратимого четырехполюсника может быть выражена через параметры холостого хода и короткого замыкания. Например, для коэффициентов 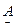 получаем:
получаем:
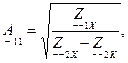
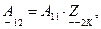
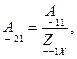
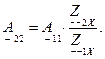
Основываясь на наше задание начнем расчет 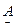 - параметров с того, что рассчитаем сопротивления холостого хода и короткого замыкания для заданной цепи (рисунок 4.2).
- параметров с того, что рассчитаем сопротивления холостого хода и короткого замыкания для заданной цепи (рисунок 4.2).
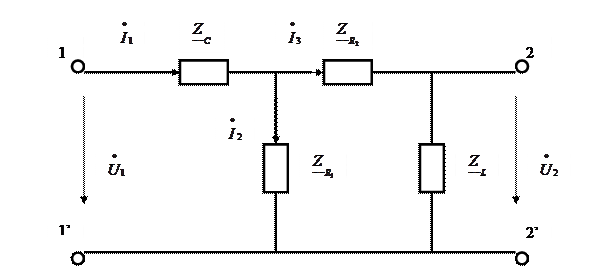
Рисунок 4.2 – комплексная схема замещения рассчитываемой цепи
Сопротивления холостого хода цепи найдем, используя выражения (4.1) и (4.3):
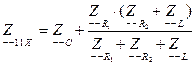 (4.1)
(4.1)
где 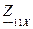 - входное сопротивление со стороны зажимов 1 -1’, в режиме
- входное сопротивление со стороны зажимов 1 -1’, в режиме
холостого хода на зажимах 2 – 2’, Ом. То есть зажимы 2 -2’ не подключены. Таким образом токи заданной цепи будут проходить через все элементы (рисунок 4.2), поэтому 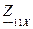 будем определять выражением (4.1).
будем определять выражением (4.1).
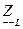 - комплексное сопротивление катушки;
- комплексное сопротивление катушки;
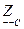 - комплексное сопротивление конденсатора;
- комплексное сопротивление конденсатора;
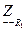 - комплексное сопротивление резистора
- комплексное сопротивление резистора 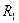 ;
;
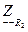 - комплексное сопротивление резистора
- комплексное сопротивление резистора 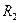 .
.
Преобразуем выражения (4.1) и подставляем численные значения для нахождения комплексного сопротивления 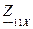 :
:
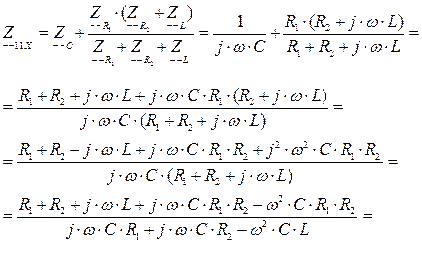

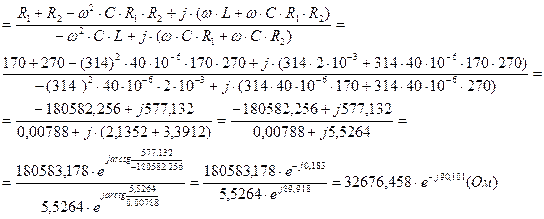
(4.2)
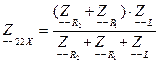 (4.3)
(4.3)
где 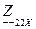 - сопротивление со стороны зажимов 2 – 2’, в режиме холостого хода на зажимах 1 – 1’, Ом. То есть зажимы 1 – 1’ разомкнуты и ток не будет проходить через конденсатор, а будет протекать в направлении резистора
- сопротивление со стороны зажимов 2 – 2’, в режиме холостого хода на зажимах 1 – 1’, Ом. То есть зажимы 1 – 1’ разомкнуты и ток не будет проходить через конденсатор, а будет протекать в направлении резистора 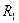 (рисунок 4.4), поэтому
(рисунок 4.4), поэтому 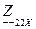 будет определяться выражением (4.3).
будет определяться выражением (4.3).
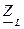 - комплексное сопротивление катушки;
- комплексное сопротивление катушки;
 - комплексное сопротивление резистора
- комплексное сопротивление резистора 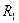 ;
;
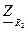 - комплексное сопротивление резистора
- комплексное сопротивление резистора 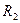 .
.

Рисунок 4.4 – Распределение токов в режиме холостого хода
Аналогичным образом преобразуем выражение (4.3) и подставляем численные значения:
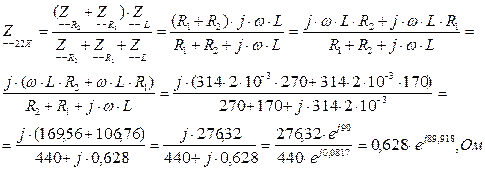 (4.4)
(4.4)
Сопротивления короткого замыкания цепи найдем, используя выражения (4.5) – (4.7):
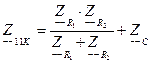 (4.5)
(4.5)
где 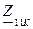 - входное сопротивление со стороны зажимов 1 – 1’, при закороченных зажимах 2 – 2’, Ом. Так как зажимы 2 – 2’ соединены между собой, соответственно ток третий, протекающий через резистор
- входное сопротивление со стороны зажимов 1 – 1’, при закороченных зажимах 2 – 2’, Ом. Так как зажимы 2 – 2’ соединены между собой, соответственно ток третий, протекающий через резистор 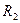 не будет проходить через катушку, а пойдет по пути наименьшего сопротивления (рисунок 4.3), поэтому
не будет проходить через катушку, а пойдет по пути наименьшего сопротивления (рисунок 4.3), поэтому 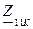 будет определяться выражением (4.5);
будет определяться выражением (4.5);
 - комплексное сопротивление резистора
- комплексное сопротивление резистора 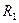 ;
;
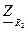 - комплексное сопротивление резистора
- комплексное сопротивление резистора 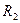 ;
;
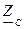 - комплексное сопротивление конденсатора.
- комплексное сопротивление конденсатора.
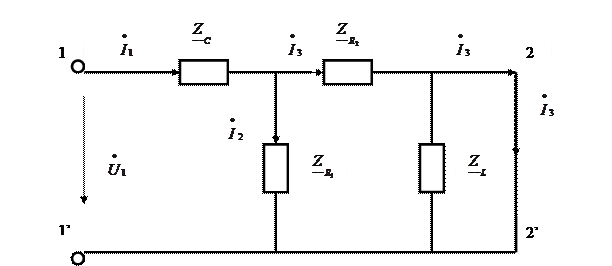
Рисунок 4.5 – Распределение токов в режиме короткого замыкания со стороны зажимов 2 – 2’
Преобразуем выражения (4.5) и подставляем численные значения для нахождения комплексного сопротивления 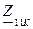 :
:
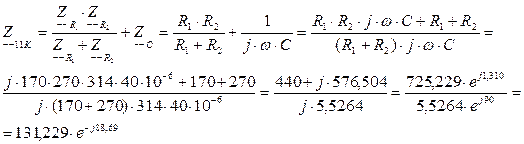 (4.6)
(4.6)
 (4.7)
(4.7)
где 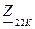 - входное сопротивление со стороны зажимов 2 – 2’, в режиме короткого замыкания на зажимах 1 – 1’, Ом. То есть зажимы 1 – 1’ соединены между собой и токи, протекающие в заданной схеме, будут проходить через все элементы цепи (рисунок 4.4). Поэтому
- входное сопротивление со стороны зажимов 2 – 2’, в режиме короткого замыкания на зажимах 1 – 1’, Ом. То есть зажимы 1 – 1’ соединены между собой и токи, протекающие в заданной схеме, будут проходить через все элементы цепи (рисунок 4.4). Поэтому 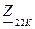 будет определяться выражением (4.7).
будет определяться выражением (4.7).
 - комплексное сопротивление резистора
- комплексное сопротивление резистора 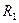 ;
;
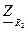 - комплексное сопротивление резистора
- комплексное сопротивление резистора 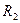 ;
;
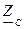 - комплексное сопротивление конденсатора;
- комплексное сопротивление конденсатора;
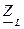 - комплексное сопротивление катушки.
- комплексное сопротивление катушки.
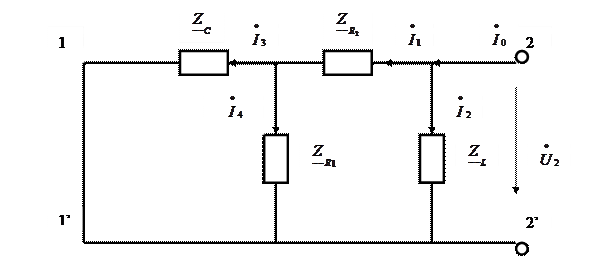
Рисунок 4.6 – Распределение токов в режиме короткого замыкания со стороны зажимов 1 -1’
Преобразуем выражения (4.7) и подставляем численные значения для нахождения комплексного сопротивления 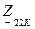 :
:
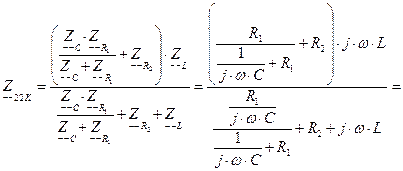

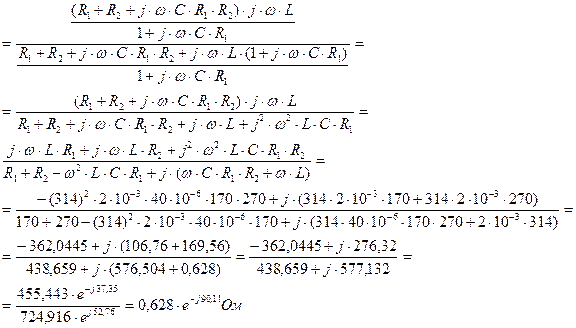
(4.8)
Используя значения 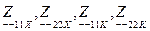 определяю
определяю 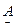 - параметры по формулам (4.9) – (4.12):
- параметры по формулам (4.9) – (4.12):
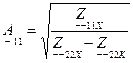 (4.9)
(4.9)
где 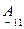 - коэффициент передачи
- коэффициент передачи  по напряжению;
по напряжению;
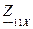 - входное сопротивление со стороны зажимов 1 -1’, в режиме
- входное сопротивление со стороны зажимов 1 -1’, в режиме
холостого хода на зажимах 2 – 2’, Ом;
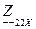 - сопротивление со стороны зажимов 2 – 2’, в режиме холостого хода на зажимах 1 – 1’, Ом;
- сопротивление со стороны зажимов 2 – 2’, в режиме холостого хода на зажимах 1 – 1’, Ом;
 - входное сопротивление со стороны зажимов 2 – 2’, в режиме короткого замыкания на зажимах 1 – 1’, Ом;
- входное сопротивление со стороны зажимов 2 – 2’, в режиме короткого замыкания на зажимах 1 – 1’, Ом;
Подставляем ранее вычисленные значения сопротивлений (4.2), (4.4) и (4.8) в выражение (4.9) и вычисляем:
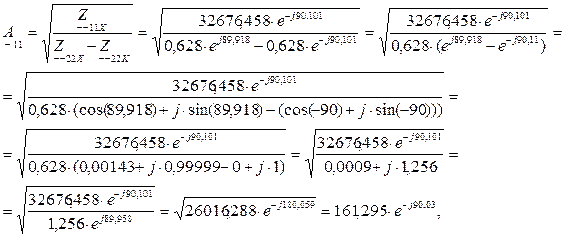
(4.10)
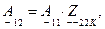 (4.11)
(4.11)
где  - передаточное сопротивление, Ом;
- передаточное сопротивление, Ом;
 - входное сопротивление со стороны зажимов 2 – 2’, в режиме короткого замыкания на зажимах 1 – 1’, Ом.
- входное сопротивление со стороны зажимов 2 – 2’, в режиме короткого замыкания на зажимах 1 – 1’, Ом.
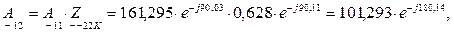 (4.12)
(4.12)
 (4.13)
(4.13)
где 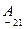 - передаточная проводимость, См;
- передаточная проводимость, См;
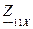 - входное сопротивление со стороны зажимов 1 -1’, в режиме
- входное сопротивление со стороны зажимов 1 -1’, в режиме
холостого хода на зажимах 2 – 2’, Ом;
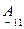 - коэффициент передачи
- коэффициент передачи  по напряжению.
по напряжению.
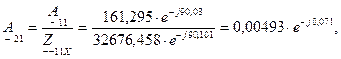 (4.14)
(4.14)
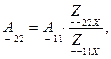 (4.15)
(4.15)
где 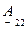 - отношение токов при режиме короткого замыкания одних из зажимов;
- отношение токов при режиме короткого замыкания одних из зажимов;
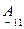 - коэффициент передачи
- коэффициент передачи  по напряжению;
по напряжению;
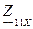 - входное сопротивление со стороны зажимов 1 -1’, в режиме
- входное сопротивление со стороны зажимов 1 -1’, в режиме
холостого хода на зажимах 2 – 2’, Ом;
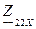 - сопротивление со стороны зажимов 2 – 2’, в режиме холостого хода на зажимах 1 – 1’, Ом.
- сопротивление со стороны зажимов 2 – 2’, в режиме холостого хода на зажимах 1 – 1’, Ом.
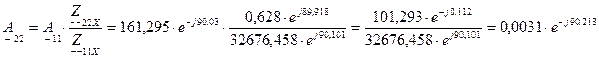
(4.16)
Проверяем правильность расчетов 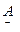 - параметров, используя тождество (4.13):
- параметров, используя тождество (4.13):
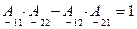 (4.17)
(4.17)
где 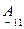 - коэффициент передачи
- коэффициент передачи  по напряжению;
по напряжению;
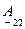 - отношение токов при режиме короткого замыкания одних из зажимов;
- отношение токов при режиме короткого замыкания одних из зажимов;
 - передаточное сопротивление, Ом;
- передаточное сопротивление, Ом;
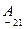 - передаточная проводимость, См.
- передаточная проводимость, См.
Подставляем численные значения полученных 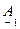 - параметров (4.10), (4.12), (4.14), (4.16) в выражение (4.17) и получаем:
- параметров (4.10), (4.12), (4.14), (4.16) в выражение (4.17) и получаем:
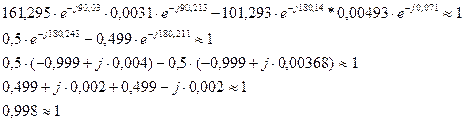
(4.18)
Можно сделать вывод, что расчеты выполнены правильно, с учетом допустимой погрешности.
5 Расчет характеристической (собственной) постоянной передачи четырехполюсника
Условие, когда четырехполюсник нагружен соответствующим характеристическим сопротивлением, называется условием согласованной нагрузки или согласованного включения.
Характеристические сопротивления будут выглядеть следующим образом:

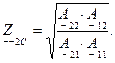
|
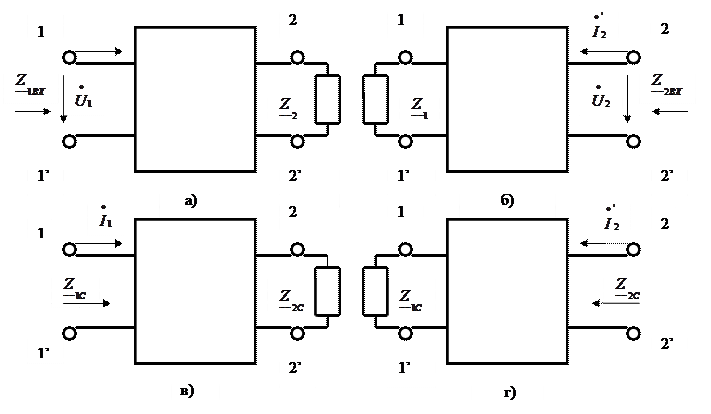
Рисунок 5.1 - Несимметричный четырехполюсник при прямой и обратной передаче (а и б - произвольная нагрузка; в и г - согласованная нагрузка)
Положим, что сопротивления 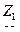 и
и 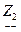 в схемах рисунок 5.1 а и б подобраны таким образом, что
в схемах рисунок 5.1 а и б подобраны таким образом, что 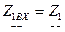 и
и 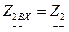 . Иначе говоря, будем считать, что существуют два сопротивления:
. Иначе говоря, будем считать, что существуют два сопротивления: 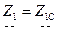 и
и 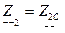 , которые удовлетворяют следующему условию: входное сопротивление
, которые удовлетворяют следующему условию: входное сопротивление 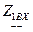 четырехполюсника, нагруженного сопротивлением
четырехполюсника, нагруженного сопротивлением 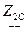 , равно
, равно  (рисунок 5.1 в); входное сопротивление
(рисунок 5.1 в); входное сопротивление 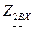 четырехполюсника, нагруженного сопротивлением
четырехполюсника, нагруженного сопротивлением  , равно
, равно 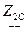 (рисунок 5.1, г).
(рисунок 5.1, г).
Такие два сопротивления называются характеристическими сопротивлениями несимметричного четырехполюсника.
Условие, когда четырехполюсник нагружен соответствующим характеристическим сопротивлением, называется условием согласованной нагрузки или согласованного включения.
Предположим, что
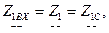
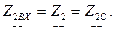
Тогда получим:
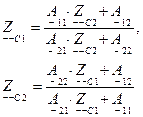
Совместное решение этих уравнений относительно 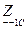 и
и 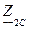 дает:
дает:
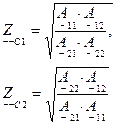
Введем для рассматриваемого обратимого четырехполюсника новый параметр  , удовлетворяющий условиям:
, удовлетворяющий условиям:
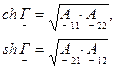
Эти условия всегда осуществимы, так как параметр  может быть комплексным. Кроме того, эти условия взаимно дополняют друг друга, так как имеющая место связь между коэффициентами соответствует тригонометрической формуле:
может быть комплексным. Кроме того, эти условия взаимно дополняют друг друга, так как имеющая место связь между коэффициентами соответствует тригонометрической формуле:
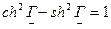
Параметр  в общем случае комплексный;
в общем случае комплексный; 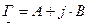 называется характеристической постоянной передачи четырехполюсника. Это — третий характеристический параметр обратимого четырехполюсника. Его действительная часть - А называется постоянной ослабления четырехполюсника, а мнимая часть В — постоянной фазы.
называется характеристической постоянной передачи четырехполюсника. Это — третий характеристический параметр обратимого четырехполюсника. Его действительная часть - А называется постоянной ослабления четырехполюсника, а мнимая часть В — постоянной фазы.
Децибел – единица затухания, в 10 раз меньшая бела. Затухание 1 дБ соответствует уменьшению полной мощности в 1, 26 раза или уменьшению напряжения и тока в 1, 12 раза. Затуханию 1 Нп соответствует уменьшение амплитуды и действующего значения напряжения или тока в 2, 718 раза.
Расчет этой характеристики будем реализовывать двумя способами, для того чтобы можно было проверить правильность расчета. В обоих случаях, при правильном решении, должны совпадать результаты решений.