
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 6
|
|
Организация графических данных в САПР.
Для эффективного функционирования программного обеспечения САПР необходима организация данных, основанная на модели объекта проектирования. Она включает в себя:
− моделирование структур данных;
− организацию их хранения;
− доступ к ним.
Под моделью объекта проектирования понимают такое представления данных, которое наиболее адекватно отображает характерные свойства реального объекта, существенные для процесса проектирования.
Существуют два типа моделей:
1. двухмерные, так называемые графические изображения (ГИ), которые позволяют формировать и изменять чертежи.
2. трехмерные модели, так называемые пространственные геометрические модели (ПГМ), которые служат для представления проектируемого изделия в трех измерениях. Трехмерные модели делятся на три типа:
− каркасные (проволочные); в них хранятся координаты вершин и соединяющие их рёбра.
− поверхностные (полигональные); задаются поверхностными плоскостями, поверхностями вращения, поверхностями сдвига и т.д.
− объемные (твердотельные) модели; обеспечивают представление изделия с использованием логической связанности информации.
Следует заметить, что многие системы низкого уровня, обладают возможностью каркасного и поверхностного моделирования, а их последние версии — даже твердотельного моделирования.
Средства трехмерного моделирования
Любая из проекций ортогонального чертежа (двухмерная модель) распознается системой как плоский элемент, ограниченный некоторым количеством точек с определенными координатами X и У. Трехмерная модель описывается точками с третьей координатой
по оси Z. На рисунке 5 показана трехмерная модель куба.
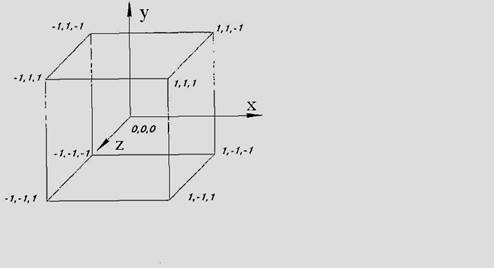
Рис. 5. Трехмерная модель куба
На плоском экране (или чертеже) получается лишь мнимый образ трехмерного куба, однако в памяти компьютера этот куб характеризуется реальной трехмерной формой. Чертеж фигуры, показанный на рис. 6, распознается двухмерной системой как три полностью независимых рисунка, ограниченных в общем восемнадцатью точками.

Рис. 6. Ортогональный чертеж фигуры
Трехмерная система распознает их как три проекции одного и того же объекта, имеющего в пространстве двенадцать поименованных вершин (см. рис.7).
И даже если были представлены только два вида, например XZ и XY, то виды YZ и XYZ могут быть автоматически восстановлены.
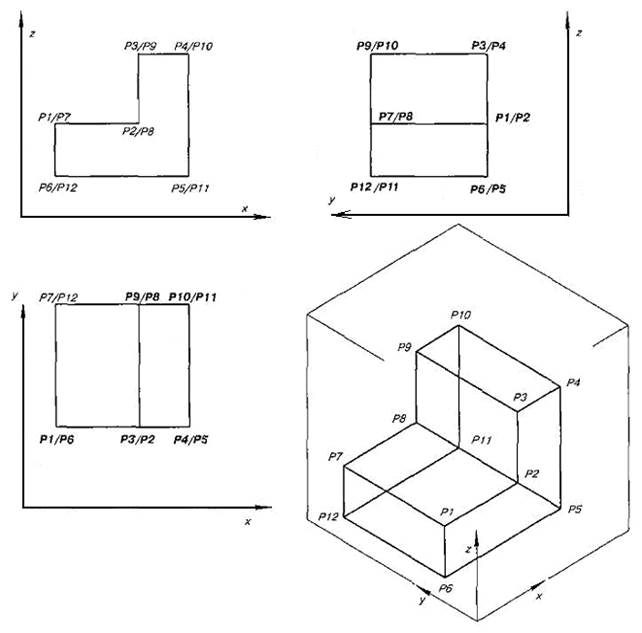
Рис. 7. Распознавание трёхмерной системой ортогонального чертежа.
Каркасное моделирование.
Каркасная модель полностью описывается в терминах точек и линий. В каркасных моделях хранятся координаты вершин и соединяющих их ребер. Каркасное моделирование представляет собой моделирование самого низкого уровня и имеет ряд серьезных ограничений, большинство из которых возникает из-за недостатка информации о гранях, заключенных между ребрами, и невозможности выделить внешнюю и внутреннюю области изображения твердотельного объема.
Главным фактором в ограничении применения каркасных поверхностей является неоднозначность распознавания ориентации и видимости граней каркасного изображения. Например, трехмерное изображение можно изобразить в двух видах: сверху и снизу (рис.8.).
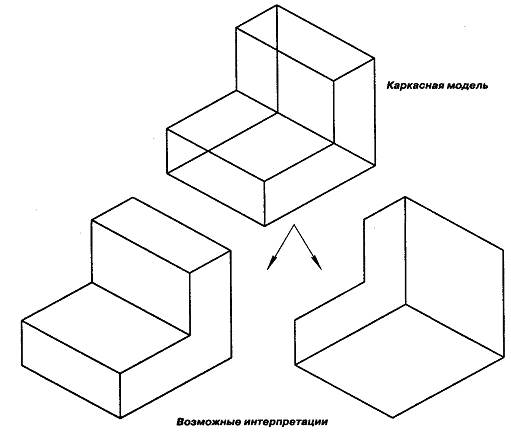
Рис.8. Возможные интерпретации модели при каркасном моделировании
Этот эффект, обусловленный природой каркасной модели, может привести к непредсказуемым результатам. В отличие от твердотельной модели, в каркасной модели нельзя отличить видимые грани геометрической формы от невидимых (скрытых).
Операцию по удалению скрытых линий можно выполнить только вручную с применением команд редактирования к каждой отдельной линии. Однако результат этой работы будет равносилен «разрушению» всей созданной каркасной конструкции, потому что линии, невидимые на одних проекциях, видимы на других. И удаление «невидимой» линии на одной проекции неизбежно повлечет за собой удаление ее на всех остальных проекциях (рис.9.)
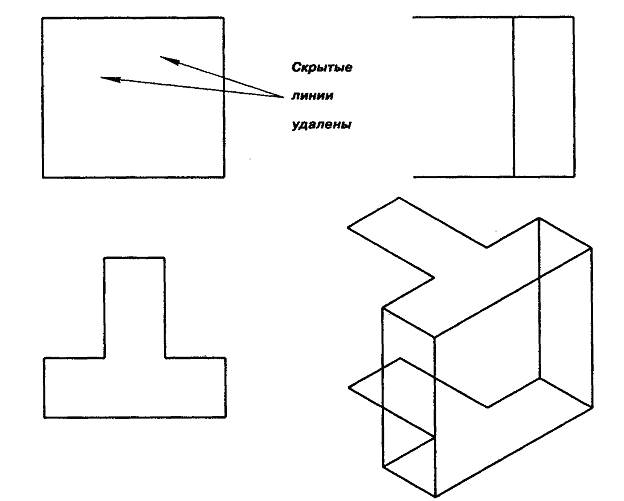
Рис. 9. Пример «разрушения» каркасной модели
Еще сложнее обстоит дело с криволинейными поверхностями. Как известно, цилиндрическая поверхность определяется перемещением образующей по некоторой направляющей, поэтому в ортогональных проекциях такая поверхность изображается посредством очерковых образующих. Естественно, что эти образующие не являются тождественными, например, на главном виде и виде слева, поэтому не распознаются как элементы каркасной модели, а значит, и не изображаются на ней.
Поверхностное моделирование
Поверхностная модель определяется с помощью точек, линий и поверхностей. Поверхностные модели задаются поверхностями вращения, плоскостями, поверхностями сдвига и т.д. Таким образом, ее можно рассматривать как модель более высокого уровня, чем каркасная модель, и, следовательно, как более гибкую и многофункциональную. Метод поверхностного моделирования наиболее эффективен при проектировании сложных криволинейных поверхностей, изготавливаемых из листового материала, например, элементов кузова автомобиля.
Поверхности образуются различными способами и могут быть разделены для целей компьютерной графики по способу их получения на элементарные геометрические поверхности, поверхности вращения, аналитические поверхности и поверхности произвольных форм (известные также как «скульптурные» поверхности или поверхности «свободных форм»).
К элементарным геометрическим поверхностям относятся поверхности, которые образуются параллельным переносом линии вдоль перпендикулярной к ней оси (рис.10.).
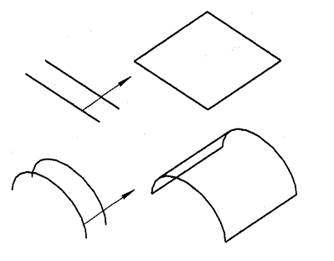
Рис. 10. Образование геометрических поверхностей
В свою очередь, поверхности могут быть преобразованы операциями параллельного переноса в трехмерные объекты (рис.11.). Следует отметить, что системы поверхностного моделирования не распознают такие формы, как твердые объемные тела. Они представляют их просто как поверхности (на рис.11. — семь плоских граней), соединенные в пространстве друг с другом некоторым образом и ограничивающие «пустой» объем.
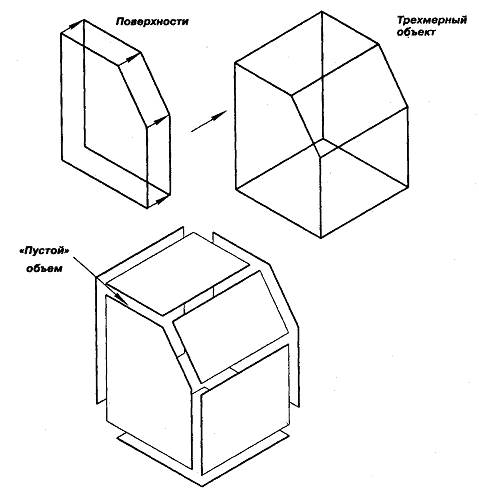
Рис.11. Образование трехмерного объекта поверхностями
Поверхности вращения могут быть легко получены вращением огибающей некоторой плоской фигуры вокруг определенной оси (рис.12.).
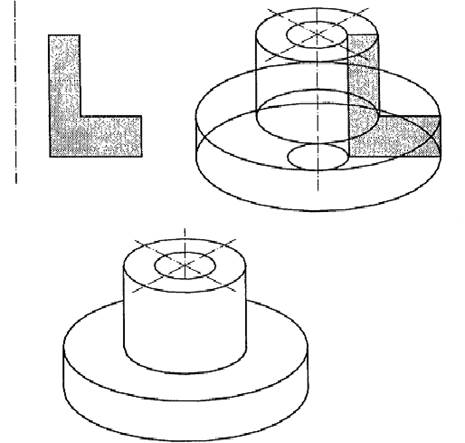
Рис.12. Пример образования поверхностей вращения
Несмотря на целый ряд достоинств метода поверхностного моделирования, его применение ограничено из-за ряда недостатков и, прежде всего, из-за сложности процедуры удаления невидимых линий и отображения внутренних областей.
Твердотельное моделирование
Твердотельная модель описывается в терминах того трехмерного объема, который занимает определяемое ею тело. Таким образом, твердотельное моделирование является единственным средством, которое обеспечивает полное и однозначное описание трехмерной геометрической формы. Этот способ моделирования представляет собой самый современный и наиболее мощный из трех указанных методов.
Неоспоримыми преимуществами твердотельной модели являются:
− полное определение объема и формы;
− обеспечение автоматического удаления невидимых (скрытых) линий;
− автоматизированное построение трехмерных разрезов проектируемого изделия, что особенно важно при анализе сложных сборочных единиц;
− автоматическое получение точных значений массы, площади поверхности, центра тяжести, момента инерции для любой детали или изделия в целом;
− повышение эффективности имитации движения инструмента или рабочих органов изделия;
− наконец, наличие разнообразной палитры цветов, управление цветовой гаммой, получение тоновых эффектов — всего того, что способствует получению качественного изображения формы.
Объёмные (твердотельные) ПГМ представляют изделие с обеспечением логической связности информации, в частности, благодаря введению понятия о материале и его физических свойствах, таких как теплопроводность, плотность и т.д.
Внутреннее представление твердотельных геометрических моделей может быть выражено его границами (гранями, рёбрами, вершинами). В этом случае используются данные трёх типов:
1. Геометрические данные. К ним относятся аналитически описанные вершины (в виде координат), а также описанные уравнениями рёбра и поверхности.
2. Топологические данные. Позволяют с помощью понятий «внутри» и «вне» определить топологию объекта.
3. Вспомогательные данные (цвет, степень прозрачности и т.д.)
Один из методов твердотельного конструирования основан на построении модели из набора базовых твердотельных примитивов, находящихся в библиотеках системы. Каждый примитив определен некоторой формой (шар, цилиндр переменного сечения, параллелепипед и т. п.), точкой привязки, исходной ориентацией и изменяемыми размерами.
Объёмные тела и графические изображения, образованные из более простых объектов называют составными геометрическими объектами.
Процесс создания составной конструкции основан на использовании булевых операций (булевы операции базируются на понятиях алгебраической теории множеств). При этом используют логические операции: объединения, пересечения и вычитания.
Действие трех булевых операций — объединения, разности и пересечения — проиллюстрировано на рисунке 13 на практических примерах твердотельных моделей:
1 – два непересекающихся тела;
2 – два пересекающихся тела;
3 – два совпадающих тела.
1 2 3
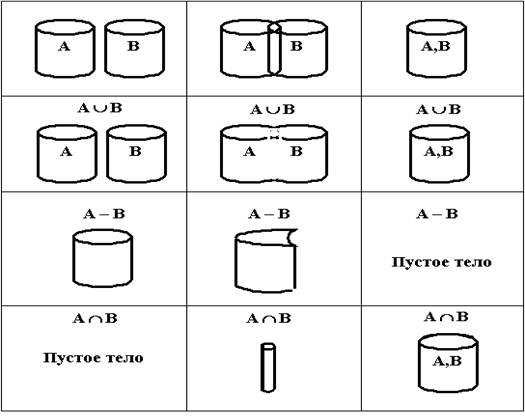
Рис. 13. Графическая интерпретация логических операций: объединения, вычитания и
пересечения.
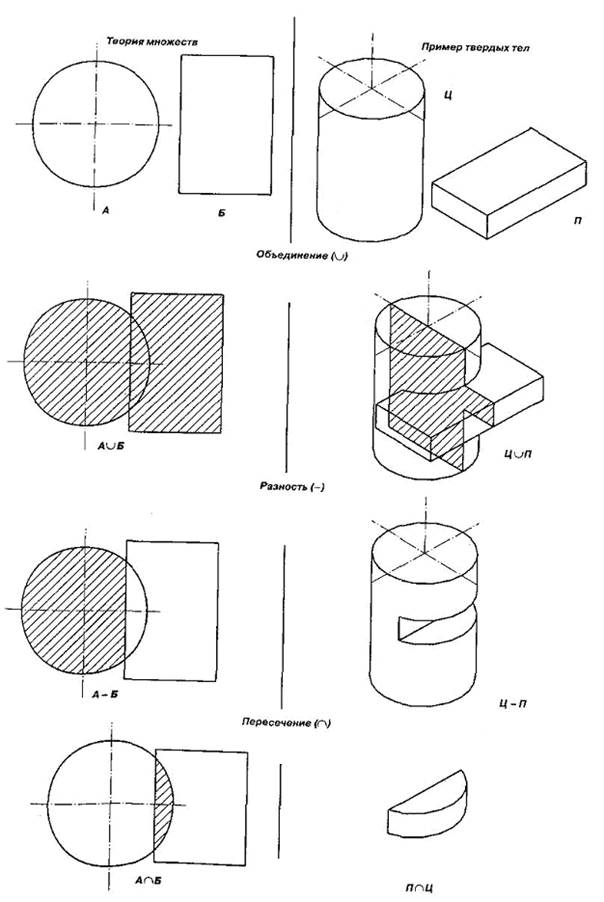
Рис. 14. Действие булевых операций в теории множеств (фигуры А и Б) и на примере твердотельных примитивов цилиндра Ц и параллелепипеда П.
Действие трех булевых операций – объединения, разности и пересечения проиллюстрировано на рисунке 14 на практических примерах твердотельных моделей.
Операция объединения (логическое «и») определяет пространство внутри внешней границы составной фигуры, полученной из двух тел. Результат объединения двух произвольных фигур А и Б представляет собой заштрихованную область А и Б. Таким образом, операция объединения определяет результирующую составную фигуру как один элемент. На этом же рисунке показано применение операции объединения для двух твердотельных примитивов (цилиндра Ц и параллелепипеда П) и проведено сечение объединения Ц U П, чтобы подчеркнуть, что образовалась новая форма, не похожая ни на цилиндр, ни на параллелепипед.
Операция разности (–) определяет пространство, оставшееся от одной фигуры после вычета общей области двух фигур. (То есть А–Б есть множество точек, принадлежащих А, но не принадлежащих Б.)
Операция пересечения (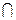 ) определяет пространство внутри границ общей области фигур (то есть множество точек, принадлежащих обеим фигурам). Например, для того чтобы показать внутренние поверхности проектируемой детали, достаточно вычесть параллелепипед из полученного изображения детали (по аналогии с вырезом в аксонометрических проекциях).
) определяет пространство внутри границ общей области фигур (то есть множество точек, принадлежащих обеим фигурам). Например, для того чтобы показать внутренние поверхности проектируемой детали, достаточно вычесть параллелепипед из полученного изображения детали (по аналогии с вырезом в аксонометрических проекциях).
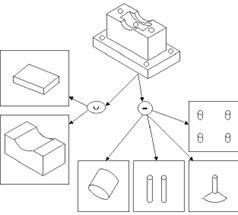
Операции сборки составных частей геометрического объекта осуществляется с использованием их представления в виде иерархической структуры, в форме дерева построения (рис.15.).
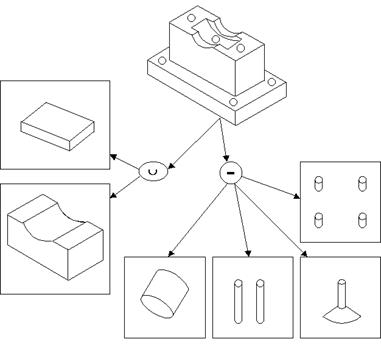
Рис. 15. Построение составного геометрического объекта из элементарных геометрических объектов с использованием логических операций: объединения и вычитания.
Для отображения реального объекта во внутримашинное представление необходимо выполнить несколько этапов. На первом этапе реальный объект подвергается абстракции, в результате которой формируется информационная модель.
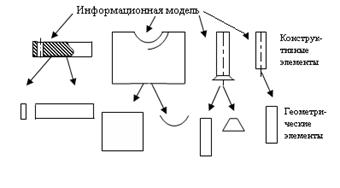
На втором этапе в информационной модели выделяют уровни структуризации данных и их взаимосвязи. Чаще всего этот процесс проводится с учётом процессов обработки информации в задаче проектирования, и таким образом осуществляется уточнение и структурирование информации с логической точки зрения. Самое важное в таком представлении получение описания не одной детали, а целого класса изделий на различных стадиях проектирования. Эта информация фиксируется в различной документации. При формировании информационных моделей используется множество конструктивныхи геометрических элементов, которые обеспечивают обработку геометрической информации для всех процессов автоматизированного проектирования. Конструктивные элементы используются для получения деталей произвольной формы. К геометрическим элементам относятся: точки, контуры, поверхности, элементарные и сложные объекты. Таким образом, при рассмотрении информационной модели с логической точки зрения строится модель данных.
На третьем этапе осуществляется процесс отображения модели данных во внутримашинное представление и формируется модель доступа. Модель доступа ориентирована на физическое размещение данных в памяти ЭВМ, в модели хранения.
На четвертом этапе определяется модель хранения, которая задает отображение данных, заданных в модели доступа, на физическую память ЭВМ и управление этими данными. Существует три способа организации данных на физических носителях: последовательный, списковый и прямой. В AutoCAD применяют списковый способ хранения геометрических данных, который позволяет хранить данные, независимо от их логической последовательности.
Т а б л и ц а 2. Отображение описания реального объекта во внутримашинное
представление.
| Этап | 2D | 3D | |
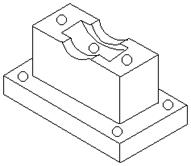
| I | Информационная модель (функциональное представление) | ||

| 
| ||
| II | Модель данных (логическое представление) | ||
| 
| ||
| III | Модель доступа | ||
| Способ доступа к данным | |||
| IV | Модель хранения | ||
| Представление данных на физическом носителе | |||
После создания полной трехмерной модели можно выполнить чертеж данного изделия в ортогональных проекциях. Сделать это позволяют программные средства автоматического получения требуемых проекций с автоматическим же нанесением размеров на соответствующие виды.
Однако прежде чем приступить к изучению и освоению всей мощи современных трехмерных систем автоматизированного проектирования, необходимо изучить общие принципы и получить некоторые навыки работы с системами более простых версий, аналогично тому, как прежде чем приступить к изучению разделов высшей математики, необходимо твердо знать целый ряд ее элементарных разделов. Поэтому в данном курсе мы будем рассматривать лишь одну область процесса проектирования — создание чертежа как такового с использованием CAD-систем (в частности в среде системы AutoCAD).
|