
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Истечение жидкости из малых отверстий в тонкой стенке сосуда в атмосферу.
|
|
Истечение жидкости из малых отверстий в тонкой стенке сосуда в атмосферу.
Отверстие можно считать малым, если соблюдается условие, а< о, 1 Н,
где а – высота отверстия; Н – напор, под которым происходит истечение.
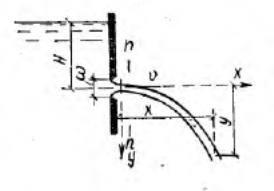
Рис. Альтшуль, с.147 рис.7.1.
Вытекающая из отверстия струя испытывает на выходе сжатие (ее поперечное сечение уменьшается).
Коэффициентом сжатия струи называется 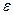 отношение площади поперечного осечени струи fсж и к площади сечения отверстия f0
отношение площади поперечного осечени струи fсж и к площади сечения отверстия f0
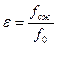 (4.1.6., с.147)
(4.1.6., с.147)
Средняя скорость в сжатом сечении струи определяется из уравнения Бернулли и представляет собой следующее соотношение
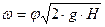 (4.1.5., с.19)
(4.1.5., с.19)
Где 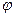 - коэффициент скорости, величина безразмерная; g– ускорение свободного падения, м/с2; ; Н – высота уровня жидкости над центром отверстия.
- коэффициент скорости, величина безразмерная; g– ускорение свободного падения, м/с2; ; Н – высота уровня жидкости над центром отверстия.
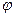 - коэффициент скорости, учитывающий потери напора, обусловленные протеканием жидкости через отверстие, характеризуемые коэффициентом местного сопротивления отверстия
- коэффициент скорости, учитывающий потери напора, обусловленные протеканием жидкости через отверстие, характеризуемые коэффициентом местного сопротивления отверстия 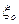
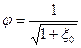 (4.1.6, с.147)
(4.1.6, с.147)
Объемный расход жидкости, вытекающий через отверстие площадью f0, при постоянном уровне жидкости в сосуде и при р0 = р составляет
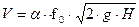
V- объемный расход жидкости, м3/с; 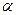 - безразмерный коэффициент расхода; р0 –давление на поверхности жидкости в сосуде, Па; р – давление в пространстве,
- безразмерный коэффициент расхода; р0 –давление на поверхности жидкости в сосуде, Па; р – давление в пространстве, 
куда вытекает струя.
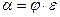
Уравнение осевой линии струи, вытекающей из отверстия в боковой стенке резервуара, имеет следующий вид

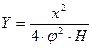
Y- длина осевой линии струи, м; х – дальность полета струи, м, Н – напор, под которым происходит истечение, м.
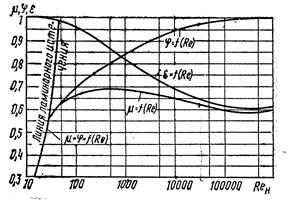
При истечении с большими значениями числа Рейнольдса (Re> 100000), что характерно для большинства случаев истечения воды и воздуха, можно при-нимать следующие значения коэффициента истечения:
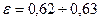

Где 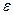 -коэффициент сжатия струи;
-коэффициент сжатия струи; 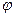 - коэффициент скорости;
- коэффициент скорости; 
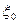 - коэффициент местного сопротивления;
- коэффициент местного сопротивления; 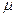 - коэффициент расхода отверстия.
- коэффициент расхода отверстия.
Время опорожнения 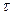 - открытого сосуда, имеющего постоянную площадь поперечного сечения f, через отверстие площадью f0может быть определено по уравнению
- открытого сосуда, имеющего постоянную площадь поперечного сечения f, через отверстие площадью f0может быть определено по уравнению
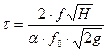 (4.1.5., с.19)
(4.1.5., с.19)
Н – начальный уровень жидкости над отверстием, м; f- площадь поперечного сечения сосуда, м2; f0– площадь поперечного сечения отверстия, м2. 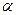 - безразмерный коэффициент расхода.
- безразмерный коэффициент расхода.
При истечении в атмосферу из большого резервуара через конический насадок с плавно округленным входом под постоянным статическим напором Н, предполагая квадратичную зону истечения и пренебрегая неравномерностью распределения скоростей по сечению, коэффициент расхода 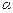 и
и 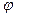 - коэффи-
- коэффи-  циент скорости можно принять равными.
циент скорости можно принять равными.
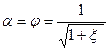 (4.1.8., с. 128)
(4.1.8., с. 128)
Где 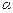 - коэффициент расхода отверстия;
- коэффициент расхода отверстия; 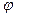 - коэффициент скорости;
- коэффициент скорости; 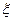


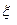 - коэффициент сопротивления насадка.
- коэффициент сопротивления насадка.
Истечение из больших отверстий в атмосферу.
Для отверстий любой формы сечения расход можно приближенно определить по следующей формуле
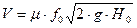 Альтшул.ьстр.150
Альтшул.ьстр.150
Где 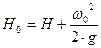
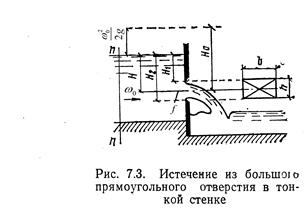
Рис.1 Истечение из большого прямоугольного отверстия в тонкой стенке
Альтшуль, стр.150 рис.7.3
Н- напор над центром тяжести отверстия; 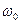 - скорость подхода к отверстию;
- скорость подхода к отверстию;
V- расход, м3 /с; 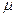 - коэффициент расхода отверстия; f- площадь отверстия, м2.
- коэффициент расхода отверстия; f- площадь отверстия, м2.
Для прямоугольного отверстия в вертикальной стене расход можно определить рис.7.3.
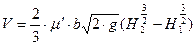 Альтшуль, 150
Альтшуль, 150
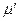 - коэффициент расхода отверстия, имеет примерно те же значения, что и для малых отверстий, b – ширина отверстия, м; Н1- расстояние от свободной поверхности до кромки отверстия, м; Н2 - расстояние от свободной поверхности до центра отверстия, м.
- коэффициент расхода отверстия, имеет примерно те же значения, что и для малых отверстий, b – ширина отверстия, м; Н1- расстояние от свободной поверхности до кромки отверстия, м; Н2 - расстояние от свободной поверхности до центра отверстия, м.
При наклоне стенки к горизонту под углом 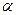 - расход можно определить
- расход можно определить
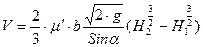
Истечение под уровень (затопленное истечение)(рис.7.4)
Альтшуль, стр.150, рис.7.4.
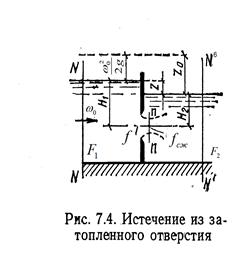 .
.
Расход через затопленное отверстие (рис.7.4) определяется
Где 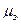 - коэффициент расхода затопленного отверстия, определяемый по формуле Альтшуля. 151 с
- коэффициент расхода затопленного отверстия, определяемый по формуле Альтшуля. 151 с
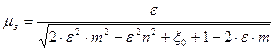 Альтшуль, стр.151
Альтшуль, стр.151
Где 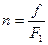 - отношение площади отверстия f к площади сечения F1 потока выше отверстия;
- отношение площади отверстия f к площади сечения F1 потока выше отверстия; 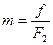 то же, ниже отверстия.
то же, ниже отверстия. 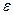 - коэффициент сжатия струи и коэффициент сопротивления
- коэффициент сжатия струи и коэффициент сопротивления 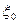 при истечении через затопленное отверстие практически не отличаются от соответствующих коэффициентов при истечении через незатопленное отверстие.
при истечении через затопленное отверстие практически не отличаются от соответствующих коэффициентов при истечении через незатопленное отверстие.
Для отверстий малых размеров по сравнению с резервуарами (n 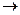 0; m
0; m 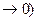
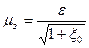 то есть совпадает со значением коэффициента расхода при незатопленном истечении (истечение в атмосферу).
то есть совпадает со значением коэффициента расхода при незатопленном истечении (истечение в атмосферу).
Истечение из насадков и коротких труб.
Насадком называется короткая труба L=(3-4) d, присоединенная к отверстию для изменения характеристик истечения (по сравнению с истечением из отверстия). Формула расхода V для насадков та же, что и для отверстий в тонкой стенке.
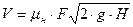 Альтшуль, стр.151
Альтшуль, стр.151
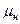 - коэффициент расхода, отнесенный к выходному сечению насадка;; F- площадь выходного отверстия насадка; Н- напор над центом тяжести выходного отверстия (или разность уровней верхнего и нижнего горизонтов воды при затопленном насадке). Значения коэффициентов расхода
- коэффициент расхода, отнесенный к выходному сечению насадка;; F- площадь выходного отверстия насадка; Н- напор над центом тяжести выходного отверстия (или разность уровней верхнего и нижнего горизонтов воды при затопленном насадке). Значения коэффициентов расхода 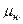 (а также коэффициентов
(а также коэффициентов 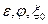 ) принимаются различными для насадков разных типов. Для квадратичной области сопротивления (когда коэффициенты истечения не зависят от числа Рейнольдса) значения коэффициентов истечения насадков.
) принимаются различными для насадков разных типов. Для квадратичной области сопротивления (когда коэффициенты истечения не зависят от числа Рейнольдса) значения коэффициентов истечения насадков. 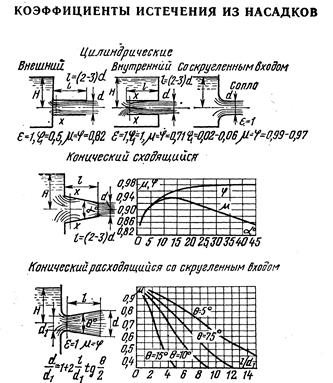
При расчете коротких трубопроводов следует учитывать не только местные потери напора, но и потери на трение. Расход жидкости из трубопровода постоянного диаметра d длиной L, работающего под напором Н, определяют по формуле, аналогичной формулам истечения из насадков
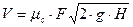 Альтшуль стр.151
Альтшуль стр.151
 - коэффициент расхода системы:
- коэффициент расхода системы:
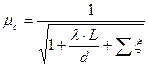 Альтшуль, стр.151
Альтшуль, стр.151
Где 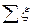 - сумма всех коэффициентов местных сопротивлений данного трубопровода;
- сумма всех коэффициентов местных сопротивлений данного трубопровода; 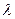 - коэффициент гидравлического трения трубопровода.
- коэффициент гидравлического трения трубопровода.
При истечении под уровень (затопленное истечение) коэффициент расхода системы  необходимо принимать:
необходимо принимать:
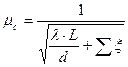
 Альтшуль, стр.152
Альтшуль, стр.152
Равновесие жидкости в движущихся сосудах
При равновесии жидкости в сосуде, равномерно вращающемся относительно вертикальной оси. Поверхность уровня представляет собой конгруэнтные (две геометрические фигуры называются конгруэнтными, если одну из них можно совместить с другой, изменив только ее положение в пространстве) парабо-лоиды вращения, ось которых совпадают с осью вращения сосудов.
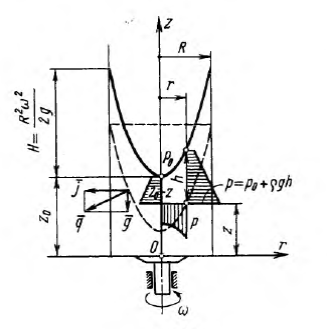
Рис. 1.Поверхность уровня параболоида вращения
Уравнение поверхности уровня (в частности свободной поверхности жидкости)
во вращающихся вместе с сосудом цилиндрических координатах (r, z) имеет вид
z- z0= w2r2/(2g) (Подвидз4.1.8., с.78)
где z, r– координаты любой точки поверхности уровня; z0 – вертикальная координата вершины параболоида поверхности уровня; w– угловая скорость сосуда.
Высота параболоида определяется;
H= w2R2/ (2g) (4.1.8., с.78)
Где H- высота параболоида, м; R– радиус сосуда, м; w– угловая скорость сосуда.
Закон распределения давления в жидкости выражается уравнением;
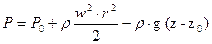 (4.1.8., с.78)
(4.1.8., с.78)
Где Р0 – известное давление в точке жидкости с координатами r0, z0; Р – давление в произвольной точке жидкости с координатами r, z.
Избыточное давление в точках на глубине h под параболоидом пьезометрической поверхности (в открытом сосуде – под параболоидом свободной поверхности)
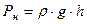
Положение свободной поверхности жидкости в сосуде (координата z0вершины параболоида) при заданной угловой скорости определяется объемом находящейся в нем жидкости, при этом используются следующие соотношения:
а) объем параболоида вращения равен половине произведения площади его основания на высоту:
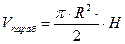 (4.1.8., с.79)
(4.1.8., с.79)
где Vпараб. – объем параболоида вращения; R – радиус сосуда; Н – высота параболоида.
Объем жидкости во вращающемся цилиндрическом сосуде в случае, когда свободная поверхность жидкости пересекает дно сосуда, вычисляется по формуле
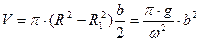
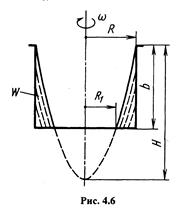
При достаточно большом значении угловой скорости 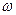 - пьезометрическая поверх поверхность пересекает крышку сосуда (параболоида) и в ее центральной части возникает вакуум, имеющий максимум на оси (точка О). Когда абсолютное давление в точке О упадет до давления насыщенных паров жидкости Рр.п, произойдет разрыв ее сплошности, и равновесие жидкости в сосуде нарушится. Значение угловой скорости, соответствующей этому явлению можно определить по следующей зависимости
- пьезометрическая поверх поверхность пересекает крышку сосуда (параболоида) и в ее центральной части возникает вакуум, имеющий максимум на оси (точка О). Когда абсолютное давление в точке О упадет до давления насыщенных паров жидкости Рр.п, произойдет разрыв ее сплошности, и равновесие жидкости в сосуде нарушится. Значение угловой скорости, соответствующей этому явлению можно определить по следующей зависимости

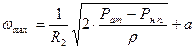 Подвидз, стр.84
Подвидз, стр.84
Изменение пропускной способности трубопроводов в процессе их эксплуатации
При проектировании напорных трубопроводов необходимо учитывать снижение пропускной способности в период эксплуатации. Например, для трубопроводов водоснабжения до 50% расчетной и даже ниже. Вследствие коррозии и инкрустации (образование отложений в трубах) шероховатость труб увеличивается, что можно определить по следующей зависимости (Альтшуль, с.103) еt = е0 + a t
Где еt – абсолютная шероховатость, мм, через t лет эксплуатации; е0 – абсолютная шероховатость, мм, для новых труб (в начале эксплуатации); a – коэффициент, характеризующий быстроту возрастания шероховатости, мм/год.
Значение коэффициента a зависит от материала труб, свойства перекачиваемой жидкости. В таблице № 1приводятся значения a в зависимости от физико- химических свойств транспортируемой воды. (Альтшуль, с.104)
Значение
a – коэффициента, характеризующий быстроту возрастания шероховатости, мм/год в зависимости от физико – химических свойств транспортируемой воды
. (Альтшуль, с.104)
Таблица 1
| Коррозионное воздействие | Характеристика природных вод | a - мм/год (в скобках даны средние значения) |
| Слабое | Слабоминерализованные некоррозионные воды с незначительным содержанием органических веществ и растворенного железа | 0, 005 - 0, 055 (0, 025) |
| Умеренное | Слабоминерализованные коррозионные воды; воды, содержащие органические вещества и растворенное железо в количестве меньше 3 мг/л | 0, 055 -0, 18 (0, 07) |
| Значительное | Коррозионные воды с содержанием железа более 30 мг/л с малым содержанием хлоридов и сульфатов | 0, 18 – 0, 40 (0, 20) |
| Сильное | Коррозионные воды с большим содержанием хлоридов и сульфатов (больше 500 – 700 мг/л; необработанные воды с большим содержанием органических веществ) | 0, 40 – 0, 60 (0, 51) |
| Очень сильное | Воды со значительной карбонатной и малой постоянной жесткостью, с плотным остатком более 2000 мг/л; сильно минерализованная и коррозионные | От 0, 6 до 1 |
Определение коэффициента гидравлического трения 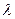 при турбулентном течении в напорных трубопроводах рекомендуются формулы Колбрука и Альтшуля, стр.
при турбулентном течении в напорных трубопроводах рекомендуются формулы Колбрука и Альтшуля, стр.
1) формула Колбрука 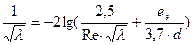
2) формула Альтшуля 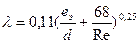

Формулы получены с помощью полуэмпирической теории турбулентности и действительны для всех однородных ньютоновских жидкостей.
Формула Колбрука приводится к формуле Прандля – Никурадзе:
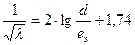 Альтшуль, стр.58
Альтшуль, стр.58
Формула Альтшуля приводится к формуле Б.Л.Шифринсона:
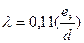 0, 25
0, 25
Где 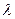 - коэффициент гидравлического трения в напорных трубопроводах круг-лого сечения при турбулентном течении; еэ – эквивалентная равномерно-зернистая абсолютная шероховатость; d– диаметр трубопровода.
- коэффициент гидравлического трения в напорных трубопроводах круг-лого сечения при турбулентном течении; еэ – эквивалентная равномерно-зернистая абсолютная шероховатость; d– диаметр трубопровода.
Эквивалентная равномерно-зернистая абсолютная шероховатость это такая высота выступов шероховатости, сложенной из песчинок одинакового размера, которая дает при подсчете по формуле Колбрука одинаковую с заданной шероховатостью величину 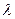
Гидравлический удар резкое увеличение давления в трубопроводе при внезапной остановке движущейся в нем жидкости. Гидравлический удар наблюдается при быстром закрывании запорных приспособлений, установленных на трубопроводах (задвижки, крана), внезапной остановке насосов, перекачивающих жидкость и т.д.
Величину повышения давления при гидравлическом ударе определяется по формуле Н.Е.Жуковского
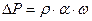
где 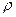 - плотность жидкости, кг/м3;
- плотность жидкости, кг/м3; 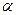 - скорость распространения ударной волны;
- скорость распространения ударной волны; 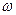 - скорость движения жидкости в трубе до закрывания запора (задвижки, крана).
- скорость движения жидкости в трубе до закрывания запора (задвижки, крана).
Скорость распространения ударной волны 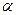 также можно определять по уравнению Н.Е.Жуковского.
также можно определять по уравнению Н.Е.Жуковского.
 Альтшуль, с.105
Альтшуль, с.105
Где Е - модуль упругости жидкости, Па; d – диаметр трубопровода, м; ЕТВ – модуль упругости материала стенки трубы; 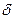 - толщина стенки трубы, м;
- толщина стенки трубы, м;
Если считать материал трубы абсолютно неупругим, (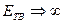 ), то выражение
), то выражение 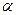 - скорость распространения ударной волны принимает следующий вид
- скорость распространения ударной волны принимает следующий вид
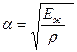
В этом случае равняется скорости распространения звука в жидкости. При обычных значениях отношения 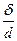 значение
значение 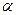 может приниматься равным 1200 м/с для стальных труб и 1000 м/с для чугунных труб.
может приниматься равным 1200 м/с для стальных труб и 1000 м/с для чугунных труб.
Основные зависимости для гидравлического расчета каналов
Расход воды V определяется по формуле Шези
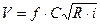 Альтшуль, 133
Альтшуль, 133
где V- расход воды, м3/с; f- поперечное сечение канала,, R – гидравлический радиус, м; i- уклон для русла; С- коэффициент Шези, м1/2/с,
Наиболее часто используются каналы трапецеидального сечения, для которых
f =(b+mh)h
b - ширина канала по дну; h – глубина наполнения канала; 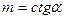 ;
; 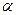 - угол откоса; m – коэффициент откоса канала.
- угол откоса; m – коэффициент откоса канала.
Смоченный периметр П канала можно определить

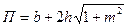
 Альтшуль, с. 134
Альтшуль, с. 134
Коэффициент откоса m выбирается из условий устойчивости откоса в зависимости от качества грунта, в котором проложен канал, а также от принятого способа крепления откоса, (значение углов откоса Альтшуль, стр.244, прилож.37)
Гидравлически наивыгоднейшее сечение канала - это сечение, у которого при заданной площади поперечного сечения канала f, заданной шероховатости стенок расход оказывается наибольшим.
При заданной площади такое сечение имеет максимальный гидравлический радиус R, т.е. минимальный смоченный периметр П. Этому требованию удовлетворяет полукруглое сечение.
Для трапецеидального канала гидравлически наивыгоднейшее сечение
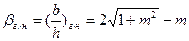
Где 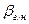 - параметр, характеризующий гидравлически наивыгоднейшее сечение.
- параметр, характеризующий гидравлически наивыгоднейшее сечение.
Для Адьтшуль, с.134)
При равномерном течении расход V, глубина h, а также форма и размеры поперечного сечения f остаются постоянными по длине потока. При расчете равномерных турбулентных течений в открытых руслах средняя скорость течения определяют по формуле Шези.
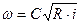 Альтшуль, с. 128
Альтшуль, с. 128
где 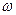 - средняя скорость, м/с, R – гидравлический радиус, м; i- уклон для русла; С- коэффициент Шези, м1/2/с, связанный с коэффициентом гидравлического трения
- средняя скорость, м/с, R – гидравлический радиус, м; i- уклон для русла; С- коэффициент Шези, м1/2/с, связанный с коэффициентом гидравлического трения 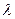 по формуле:
по формуле: 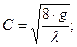
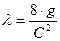 Альтшуль, с.55
Альтшуль, с.55
Для рек, формирующих русло в песчаном - гравелистом ложе, коэффициент Шези можно определить по формуле:
 - 26 Альтшуль, стр.133
- 26 Альтшуль, стр.133
Эта формула справедлива для каналов, проходящих в естественных грунтах и несущих наносы.
 Задания для контрольной работы
Задания для контрольной работы
Задание 1. Жидкость перетекает из сосуда А в сосуд В через плавно сходящийся насадок диаметром d1=100 мм (коэффициент сопротивления 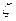 =0.08) и приставленный к нему с небольшим зазором расходящийся конический насадок выходным диаметром D2=150 мм (коэффициент потерь в диффузоре
=0.08) и приставленный к нему с небольшим зазором расходящийся конический насадок выходным диаметром D2=150 мм (коэффициент потерь в диффузоре 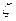 = 0.3). При заданном уровне Н1=2, 5 м в сосуде А определить уровень Н2, при котором жидкость не будет выливаться через зазор, а атмосферный воздух не будет засасываться внутрь насадка.
= 0.3). При заданном уровне Н1=2, 5 м в сосуде А определить уровень Н2, при котором жидкость не будет выливаться через зазор, а атмосферный воздух не будет засасываться внутрь насадка.
Таблица 1
| Параметры | Варианты | |||||||||
| d1, мм | ||||||||||
| D2, мм | ||||||||||
| Жид-кость | Вода | октан | толуол | бензол | ацетон |
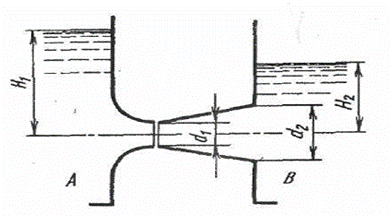
Рис.1. к заданию 1
Задание 2. Цилиндрический сосуд диаметром D1 высотой L, имеющий в верхней крышке центральное отверстие диаметром D2, заполнен до высоты В жидкостью, плотность которой при температуре t. Определить угловую скорость сосуда, при которой жидкость начнет выливаться из него. Также определить силу давления на верхнюю закраину при этой угловой скорости.
Таблица 1
| Параметры | Варианты | |||||||||
| D1, м | 1, 2 | 1, 4 | 1, 15 | 1, 25 | 1, 35 | 1, 45 | 1, 05 | 1, 6 | 1, 65 | 1, 48 |
| D2, м | 0, 6 | 0, 7 | 0, 8 | 0, 65 | 0, 55 | 0, 75 | 0, 48 | 0, 82 | 0, 9 | 0, 5 |
| t 0С | ||||||||||
| Жид-кость | Вода | октан | толуол | бензол | ацетон |
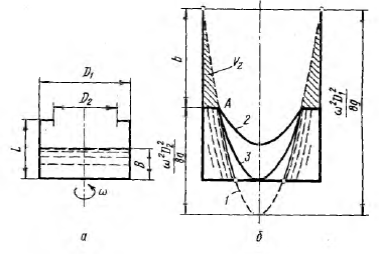
Рис. 2. К заданию 2
Задание 3. Определить расход и скорость вытекания жидкости из малого кругло-го отверстия диаметром d в боковой стенке резервуара больших размеров. Напор над центром отверстия Н, температура жидкости t.
Таблица
| Параметры | Варианты | |||||||||
| d, м | 0, 02 | 0, 04 | 0, 05 | 0, 03 | 0, 035 | 0, 04 | 0, 05 | 0, 06 | 0, 045 | 0, 048 |
| Н, м | 1, 6 | 1, 7 | 1, 8 | 1, 00 | 1, 55 | 1, 75 | 1, 48 | 1, 82 | 1, 9 | 1, 5 |
| t 0С | ||||||||||
| Жид-кость | Вода | Сероуглерод | бензол | толуол | Четыреххло-ристый углерод |
Задание 4. Определить расход и скорость истечения нефти из бака через отверстие с острыми краями диаметром d, а также коноидальный насадок того же диаметра, если напор в баке поддерживается постоянным и равным Н. Кинематическая вязкость нефти 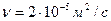
| Параметры | Варианты | |||||||||
| d, см | 1, 5 | 1, 2 | 1, 3 | 1, 35 | 1, 35 | 1, 45 | 1, 6 | 1, 8 | 2.0 | |
| Н, м | 4, 7 | 4, 8 | 5, 00 | 4, 55 | 4, 75 | 4, 48 | 4, 82 | 4, 9 | 4, 5 |
Задание 5. Определить время опорожнения цистерны с мазутом при следующих данных: Объем мазута в цистерне V, диаметр цистерны D, диаметр сливного (короткого) патрубка d. Кинематическая вязкость мазута 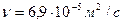 .
.
Таблица
| Пара-метры | Варианты | |||||||||
| V, м3 | ||||||||||
| d, м | 0, 1 | 0, 15 | 0, 12 | 0, 13 | 0, 14 | 0, 15 | 0, 16 | 0, 18 | 0, 2 | 0, 1 |
| D, м | 2, 8 | 3, 0 | 3, 2 | 3, 4 | 3, 6 | 2, 6 | 2, 8 | 3, 0 | 3, 2 | 3, 4 |
Задание 6. Потеря давления в стальной водопроводной трубе диаметром D м и длиной L м, бывшей в эксплуатации 12 лет, составляет 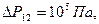 при расходе воды V=0, 2 м3/с. Температура воды 20 0С. Определить потери давления
при расходе воды V=0, 2 м3/с. Температура воды 20 0С. Определить потери давления 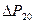 в этой же трубе, через 20 лет эксплуатации при расходе воды V1, м3/с.
в этой же трубе, через 20 лет эксплуатации при расходе воды V1, м3/с.
Таблица
| Пара-метры | Варианты | |||||||||
| V1, м3 | 0, 3 | 0, 35 | 0, 36 | 0, 353 | 0, 354 | 0, 356 | 0, 358 | 0, 362 | 0, 364 | 0, 366 |
| L, м | ||||||||||
| D, м | 0, 5 | 0, 45 | 0, 46 | 0, 47 | 0, 48 | 0, 49 | 0, 45 | 0, 46 | 0, 47 | 0, 48 |
Задание 7. Стальной новый водовод с диаметром D м, с абсолютной шероховатостью е = 0, 1мм имеет пропускную способность V1 м3/с. Вода в источнике слабоминерализованная, некоррозионная. Исследования, проведенные через два года после начала эксплуатации, показали, что абсолютная шероховатость трубопровода возросла до е = 0, 2 мм. Необходимо определить, какая будет пропускная способность водовода через 15 лет эксплуатации.
Таблица
| Пара-метры | Варианты | |||||||||
| V1, м3/с | 0, 052 | 0, 055 | 0, 056 | 0, 053 | 0, 054 | 0, 056 | 0, 058 | 0, 062 | 0, 064 | 0, 066 |
| D, м | 0, 25 | 0, 24 | 0, 26 | 0, 27 | 0, 28 | 0, 29 | 0, 25 | 0, 26 | 0, 27 | 0, 28 |
Задание 8. Потеря давления в стальной водопроводной трубе диаметром D м и длиной L м, бывшей в эксплуатации в течение 12 лет, составляет 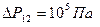 при расходе воды V12, м3/с. Температура воды 20 0С. Определить потери давления
при расходе воды V12, м3/с. Температура воды 20 0С. Определить потери давления 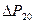 в этой трубе через 20 лет эксплуатации при расходе воды V20, м3/с
в этой трубе через 20 лет эксплуатации при расходе воды V20, м3/с
Таблица
| Пара-метры | Варианты | |||||||||
| V12, м3/с | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 54 | 0, 56 | 0, 58 | 0, 52 | 0, 64 | 0, 66 |
| D, м | 0, 45 | 0, 46 | 0, 46 | 0, 47 | 0, 48 | 0, 49 | 0, 45 | 0, 46 | 0, 47 | 0, 48 |
| V20, м3/с | 0, 3 | 0, 35 | 0, 33 | 0, 31 | 0, 32 | 0, 3 | 0, 31 | 0, 3 | 0, 31 | 0, 3 |
| L, м |
Задание 9. Определить величину повышения давления в стальной водопроводной трубе, если скорость воды в трубе до гидравлического удара была 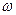 м/с, диаметр трубы D, м и толщина стенок
м/с, диаметр трубы D, м и толщина стенок 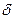 м.
м.
| Пара-метры | Варианты | |||||||||
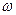 м/с м/с
| ||||||||||
| D, м | 0, 45 | 0, 46 | 0, 5 | 0, 47 | 0, 48 | 0, 49 | 0, 5 | 0, 52 | 0, 53 | 0, 5 |
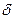 , м , м
| 0, 005 | 0, 004 | 0, 005 | 0, 005 | 0, 004 | 0, 005 | 0, 004 | 0, 005 | 0, 006 | 0, 005 |
Задание 10. Определить расход при равномерном движении воды в трапецеидальном земляном канале (суглинок), если ширина его по дну b, м, глубина h, м, заложение откосов m=1 и уклон i.
| Пара-метры | Варианты | |||||||||
| b, м | 5, 0 | 5, 5 | 6, 0 | 5, 3 | 5, 4 | 5, 6 | 5, 8 | 6, 2 | 6, 4 | 6, 6 |
| h, м | 1, 6 | 1, 8 | 1, 65 | 1, 82 | 1, 48 | 1, 56 | 1, 68 | 1, 84 | 2, 2 | 1, 78 |
| i | 0, 0003 | 0, 0004 | 0, 0002 | 0, 0004 | 0, 0006 | 0, 0005 | 0, 0008 | 0, 0003 | 0, 0005 | 0, 0003 |
Задание 11. Большая равнинная река, русло которой сформировалась из мелкого гравия и крупного песка, имеет относительно равномерное течение. Ширина реки b (м), средняя глубина на рассматриваемом участке h(м), уклон водной поверх-ности i. Определить среднюю скорость течения и расход воды V.
| Пара-метры | Варианты | |||||||||
| b, м | ||||||||||
| h, м | 2, 6 | 2, 8 | 2, 65 | 2, 82 | 2, 48 | 2, 56 | 2, 68 | 2, 84 | 2, 28 | 2, 78 |
| i | 0, 0003 | 0, 0004 | 0, 0002 | 0, 0004 | 0, 0006 | 0, 0005 | 0, 0008 | 0, 0003 | 0, 0005 | 0, 0003 |
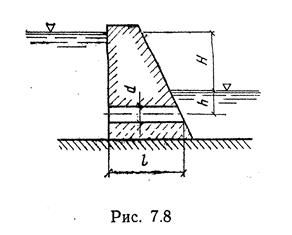
Задание 12. Водоспуск бетонной плотиныдолжен пропускать расход V, м3/с при перепаде верхнего и нижнего бьефов Н, м. Длина водоспуска L, м. Определить необходимый диаметр водоспуска dи минимальное затопление h, чтобы вакуум внутри водоспуска был Рв= 4 104Па. Температура воды 20 0С. (Водоспуск можно рассматривать как короткую трубу)
| Пара-метры | Варианты | |||||||||
| V, м3/с | 2, 0 | 1, 8 | 1, 9 | 2, 56 | 2, 65 | 2, 2 | 1, 92 | 2, 2 | 2, 19 | |
| Н, м | 12, 65 | 12, 82 | 12, 48 | 12, 56 | 12, 68 | 12, 84 | 12, 28 | 12, 78 | ||
| L, м. | 10, 5 | 10, 3 | 10, 4 | 10, 6 | 11, 5 | 11, 8 |
Приложение 1
Коэффициент гидравлического трения в зависимости от вязкости и состояния стенок трубопровода
| Материал и вид трубы | Состояние трубы | е0 – эквива-лентная рав-номерно-зер-нистая абсо-лютная шеро-ховатость, мм* |
| Тянутые трубы из стекла и цветных металлов | Новые, технически гладкие | 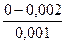
|
| Бесшовные стальные трубы | 1.Новые и чистые, тщательно уло-женные 2.После нескольких лет эксплуатации | 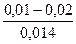
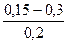
|
| Стальные трубы сварные | 1.Новые и чистые 2.С незначительной коррозией после очистки 3.Умеренно заржавевшие 4.Старые заржавевшие или с большими отложениями 5.Сильно заржавевшие или с большими отложениями | 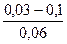

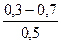
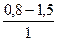
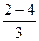
|
| Клепаные стальные трубы | 1.Легко клепаные 2. Сильно клепаные | 0, 5-3 До 9 |
мм* - под чертой даны средние значения.