Метод хорд

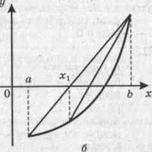
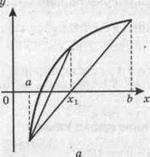
Метод хорд заключается в замене кривой у = f (x) отрезком прямой, проходящей через точки (а, f (a)) и (b, f (b)) рис. 4). Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение.

Чтобы получить расчетную формулу метода хорд, за­пишем уравнение прямой, проходящей через точки (a, f (a)) и (b, f (b)) и, приравнивая у к нулю, найдем х:

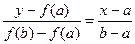Þ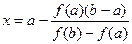

Алгоритм метода хорд:

1) пусть k = 0;

2) вычислим следующий номер итерации: k = k + 1.

Найдем очередное k -e приближение по формуле:

x_k = a - f (a)(b - a)/(f (b) - f (a)).

Вычислим f (x_k);

3) если f (x_k)= 0 (корень найден), то переходим к п. 5.

Если f (x_k) × f (b)> 0, то b = x_k, иначе a = x_k;

4) если |x_k – x_{k -1}| > ε, то переходим к п. 2;

5) выводим значение корня x_k;

6) конец.

Замечание. Действия третьего пункта аналогичны действи­ям метода половинного деления. Однако в методе хорд на каж­дом шаге может сдвигаться один и тот же конец отрезка (пра­вый или левый), если график функции в окрестности корня выпуклый вверх (рис. 4, а) или вогнутый вниз (рис. 4, б).Поэтому в критерии сходимости используется разность сосед­них приближений.

Метод секущих

Метод секущих может быть получен из метода Ньютона при замене производной приближенным выражени­ем – разностной формулой:

, ,

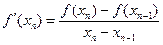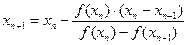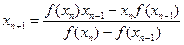. (2.7)

В формуле (2.7) используются два предыдущих при­ближения х_п и x_{n- 1}.Поэтому при заданном начальном приближении х ₀необходимо вычислить следующее приближение x ₁, например, методом Ньютона с приближенной заменой производной по формуле

,

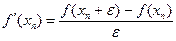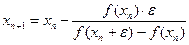
Алгоритм метода секущих:

1) заданы начальное значение х ₀и погрешность ε. Вычислим

;

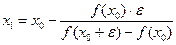2) для п = 1, 2,... пока выполняется условие | x_n – x_{n -1}| > ε, вычисляем х_{п+ 1} по формуле (2.7).

Глава 2