
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторные работы
|
|
→ номер
Цель работы: вычислить ускорение свободного падения из формулы для периода колебаний математического маятника:
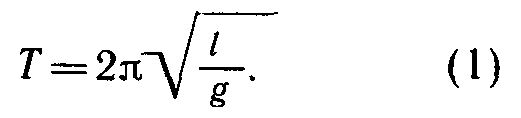
Для этого необходимо измерить период колебания и длину подвеса маятника. Тогда из формулы (1) можно вычислить ускорение свободного падения:

Средства измерения:
1) часы с секундной стрелкой;
2) измерительная лента (Δ л = 0, 5 см).
Материалы: 1) шарик с отверстием; 2) нить; 3) штатив с муфтой и кольцом.
Порядок выполнения работы
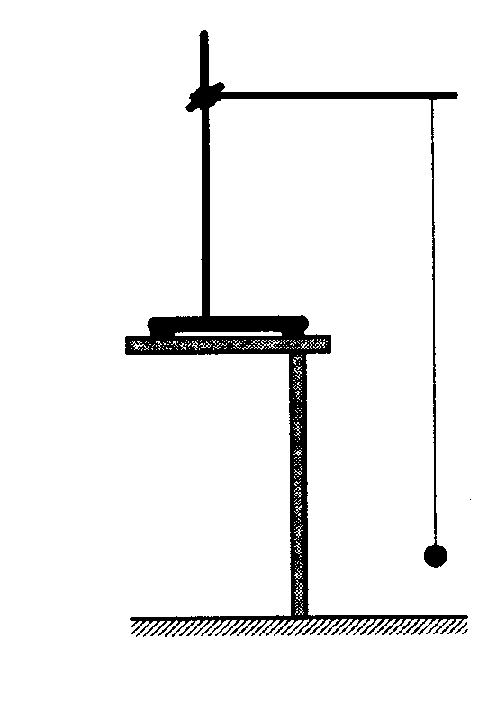
1. Установите на краю стола штатив. У его верхнего конца укрепите при помощи муфты кольцо и подвесьте к нему шарик на нити. Шарик должен висеть на расстоянии 3—5 см от пола.
2. Отклоните маятник от положения равновесия на 5—8 см и отпустите его.
3. Измерьте длину подвеса мерной лентой.
4. Измерьте время Δ t 40 полных колебаний (N).
5. Повторите измерения Δ t (не изменяя условий опыта) и найдите среднее значение Δ tср.
6. Вычислите среднее значение периода колебаний Tср по среднему значению Δ tср.
7. Вычислите значение gcp по формуле:
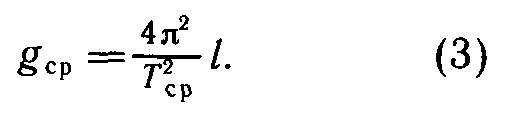
8. Полученные результаты занесите в таблицу:
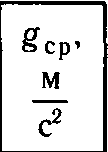
| Номер опыта | l, м | N | Δ t, с | Δ tср, с | 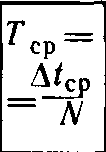
| 
|
9. Сравните полученное среднее значение для gcp со значением g = 9, 8 м/с2 и рассчитайте относительную погрешность измерения по формуле:
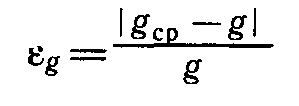
Изучая курс физики вам часто приходилось использовать в решении задач и других расчетах значение ускорения свободного падения на поверхности земли. Вы принимали значение g = 9, 81 м/с2, то есть с той точностью, которой вполне достаточно для производимых вами расчетов.
Целью данной лабораторной работы является экспериментальное установление ускорения свободного падения с помощью маятника. Зная формулу периода колебания математического маятника Т =
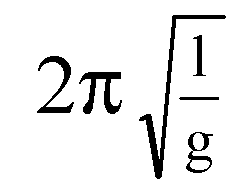
можно выразить значение g через величины, доступные простому установлению путем эксперимента и рассчитать g с некоторой точностью. Выразим
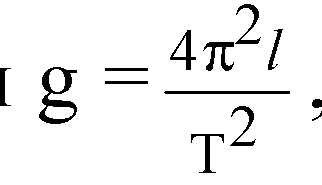
где l - длина подвеса, а Т - период колебаний маятника. Период колебаний маятника Т легко определить, измерив время t, необходимое для совершения некоторого количества N полных колебаний маятника
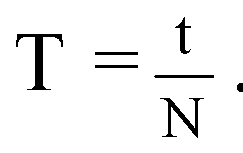
Математическим маятником называют груз, подвешенный к тонкой нерастяжимой нити, размеры которого много меньше длины нити, а масса - много больше массы нити. Отклонение этого груза от вертикали происходит на бесконечно малый угол, а трение отсутствует. В реальных условиях формула
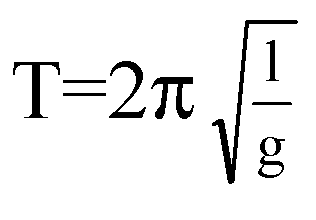
имеет приблизительный характер.
Рассмотрим такое тело (в нашем случае рычаг). На него действуют две силы: вес грузов P и сила F (упругости пружины динамометра), чтобы рычаг находился в равновесии и моменты этих сил должны быть равны по модулю меду собой. Абсолютные значения моментов сил F и P определим соответственно:
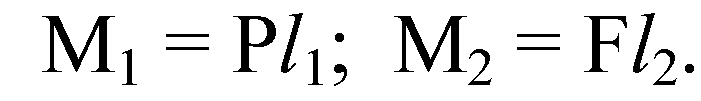
В лабораторных условиях для измерения с некоторой степенью точности можно использовать небольшой, но массивный металлический шарик, подвешенный на нити длиной 1-1, 5 м (или большей, если есть возможность такой подвес разместить) и отклонять его на небольшой угол. Ход работы целиком понятен из описания ее в учебнике.
Средства измерения: секундомер (Δ t = ±0, 5 с); линейка или измерительная лента (Δ l = ±0, 5 см)
Выполнение работы:
| № опыта | 1, м | N | t, с | tср, с | Тср | gср, м/с2 |
| 1, 5 | ||||||
| 1, 5 | 2, 475 | 9, 657 | ||||
| 1, 5 |
Вычисления:
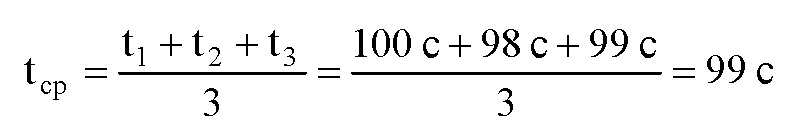
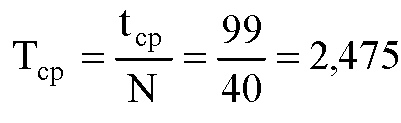
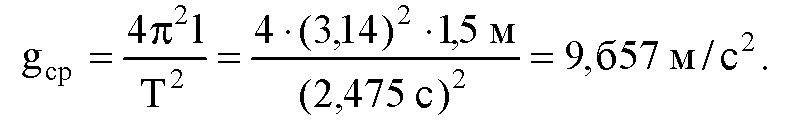
Погрешность:
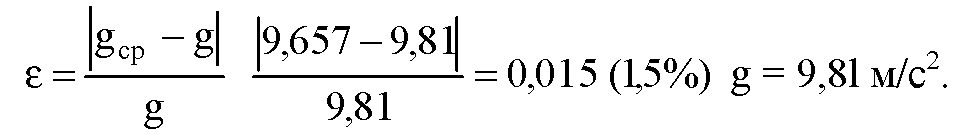
|