
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая часть. 1.1. Технико-экономическое обоснование.
|
|
1.1. Технико-экономическое обоснование.
Функциональное назначение данных антенн заключается в том, что при сравнительно малых геометрических размерах, они широкополосные и многодиапазонные за счет большого количества резонансных частот, тем самым они экономичны и малогабаритные.
Данные антенны весьма не сложные в конструкции, но в зависимости от того какие параметры необходимы их конструкцию можно усложнять.
1.2.История появления и развития ФА.
Начнем с того, что же такое фракталы?
Фракталы - геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.
Рассмотрим, какие же бывают фракталы:
-Есть сложной формы, такие как, например, эти:

-Или же простой формы:
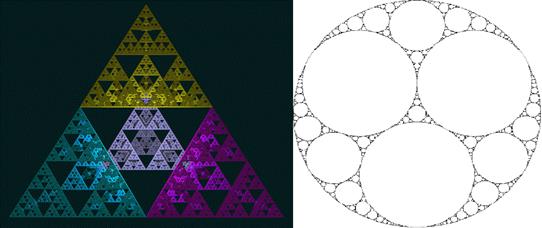
Появлению таких фракталов мы обязаны природе, ведь именно из нее мы все и узнаем, с нее все и началось.
- фракталы в природе:

Но всё-таки прижилось данное открытие в области наук: в химии, в биологии, в физике и во многих других.
История развития фрактальных антенн начал гениальный ученый Бенуа Мальденброта - французский математик, Benoî t B. Mandelbro, которому и принадлежит открытие фрактальной геометрии.
Он придумал этот термин в 1975 году, слово фрактал происходит от латинских слов fractus- дробный и frangere- ломать, а полностью оно используется как “изломанный”.
Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта”The Fractal of Nature”.
Математическая база для появления теории фракталов была заложена за много лет до рождения Бенуа Мандельброта, однако, развиться она смогла лишь с появлением вычислительных устройств.
Фрактальный рисунок не имеет идентичных элементов, но обладает подобностью в любом масштабе. Построить такое изображение с высокой степенью детализации вручную ранее было просто невозможно, на это требовалось огромное количество вычислений. Например, французский математик Пьер Жозе Луи Фату (Pierre Joseph Louis Fatou) описал это множество более чем за семьдесят лет до открытия Бенуа Мандельбротом. Если же говорить про принципы самоподобия, то о них еще было известно в трудах Лейбница и Георга Кантора.
И так вернемся к тому, что фракталы в современном обществе нашли применение для сжатия данных, фильтрации сигналов, синтеза трехмерных компьютерных моделей природных ландшафтов и во многих других сферах деятельности. Неудивительно, что во всеобщий фрактальный бум оказалась вовлеченной и теория антенн.
Первые публикации, рассматриваемые электродинамику фрактальных структур, появились еще в 80-е годы ХХ века. Начало же практическому использованию фрактального направления в антенной технике более 10 лет назад положил американский инженер Натан Коэн, ныне профессор Бостонского университета. Проживая в центре Бостона, Чтобы обойти запрет городских властей на установку наружных антенн, он решил замаскировать антенну любительской радиостанции под декоративную фигуру из алюминиевой фольги.
После серии экспериментов будущий профессор Бостонского университета понял, что антенна, сделанная по фрактальному рисунку, имеет высокий КПД и покрывает более широкий частотный диапазон по сравнению с классическими решениями. Кроме того, форма антенны в виде кривой фрактала позволяет существенно уменьшить геометрические размеры. Натан Коэн даже вывел теорему, доказывающую, что для создания широкополосной антенны достаточно придать ей форму самоподобной фрактальной кривой.
Автор запатентовал свое открытие и основал фирму по разработке и проектированию фрактальных антенн Fractal Antenna Systems, справедливо полагая, что в будущем благодаря его открытию сотовые телефоны смогут избавиться от громоздких антенн и станут более компактными.
1.3. Обзор методов и принцип построения ФА.
Основным принципом построения ФА является два метода:
Первый метод – это сгибание исходной линии, для получения необходимой формы. Так для построения кривой Коха необходимо исходную линию длинной z делится на три равные части. Далее центральный участок заменяют равносторонним треугольником со стороной z/3. Тем самым образуется ломаная, состоящая из четырех звеньев длиной z/3 каждый (рис.1). Это повторяется для каждого отдельного отрезка ломаной: в первой итерации на отрезках z/3 строятся треугольники со сторонами z/9, а на них треугольники со сторонами z/27 (вторая итерация) и так далее. Полученная кривая и есть кривая Коха.
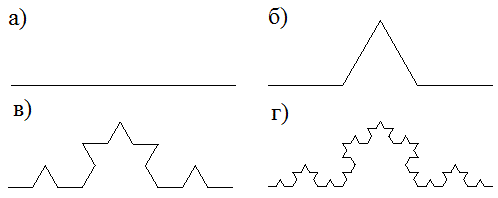
Рис.1. Построение кривой Коха: а) нулевая, б) первая, в) вторая, г) третья итерации.
Каждый шаг увеличивает длину результирующей кривой по следующему принципу:
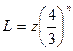 , где n- число итераций, z- длина исходной линии.
, где n- число итераций, z- длина исходной линии.
Весьма близко по своим свойствам к антенне на основе фрактала Коха- диполь, сформированный по закону ломаной Германа Минковского. При построении этой антенны вместо системы треугольников на прямой формируются меандры убывающих размеров (рис.2).
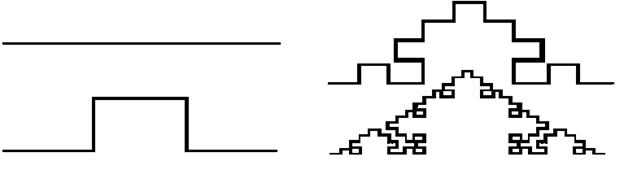
Рис.2. Построение кривой Минковского, первые три итерации.
Рассмотрим кривую Пеано. Начальным элементом здесь можно выбрать единичный квадрат, каждая из сторон которого на следующем шаге заменяется, как показано на рис. 3. Он состоит из 9 отрезков длины 1/3, соединенных под прямым углом друг к другу.
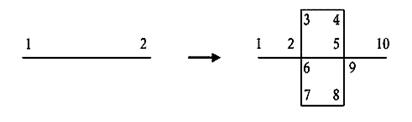

Рис.3. Построение кривой Пеано.
Цифры показывают способ обхода данной кривой. При такой геометрии неизбежны две точки соприкосновения 2-6 и 5-9. В результате исходный квадрат преобразуется так, как показано нижнем рисунке. Затем каждый из отрезков образовавшейся фигуры длиной в 1/3 преобразуется подобным же образом, и так до бесконечности. В результате возникает самоподобная непрерывная кривая, плотно заполняющая квадратную область с площадью, равной 2.
Другой тип фрактал, который можно использовать в качестве диполя - это рекурсивное дерево (рис.4). Фрактал образуют из простого монополя путем последовательного разбиения его вершин на две ветви под заданным углом (до 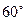 ).
).
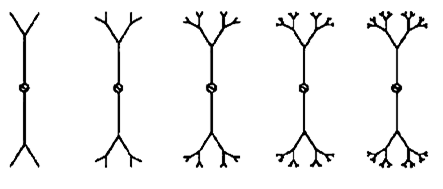
Рис.4.Построение рекурсивного дерева.
Еще одна разновидность древа – это древо Кейли являющимся одним из классических примеров фрактальных множеств. Его нулевая итерация – всего лишь отрезок прямой заданной длины 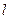 . Первая и каждая следующая нечетная итерации представляет собой два отрезка точно такой же длины
. Первая и каждая следующая нечетная итерации представляет собой два отрезка точно такой же длины 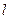 как и предыдущая итерация, расположенных перпендикулярно отрезку предыдущей итерации так, что концы его соединены с серединой отрезков.
как и предыдущая итерация, расположенных перпендикулярно отрезку предыдущей итерации так, что концы его соединены с серединой отрезков.
Вторая и каждая следующая четная итерация фрактала – это два отрезка 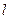 /2 в половину длины предыдущей итерации, расположенных, как и прежде, перпендикулярно предыдущей итерации.
/2 в половину длины предыдущей итерации, расположенных, как и прежде, перпендикулярно предыдущей итерации.
Результаты построения древа Кейли приведены на рисунке 5.
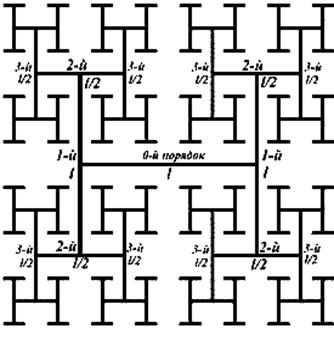
Рис. 5.Построение древа Кейли.
И наконец, кольцевой тип, который формируется следующим образом: внутри базового элемента нулевой итерации размещены 7 колец с радиусом в три раза меньше исходного элемента. Остальные параметры (ширина и толщина кольца базового элемента) оставлены без изменений. Центры 6 маленьких окружностей расположены на расстоянии R*2/3, в вершинах шестиугольника. Центр 7-й окружности совпадает с центром основной антенны. Далее в радиус каждой из 7 окружностей вписываются окружности втрое меньше предыдущего радиуса. Таким образом, полученная модель предложена на рис. 6.
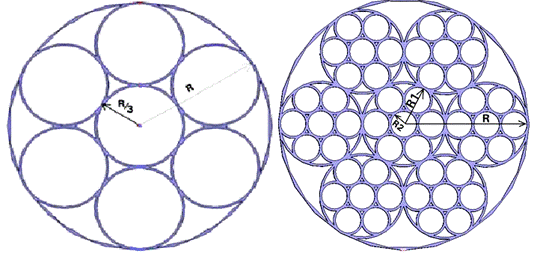
Рис.6.Фрактальная антенна кольцевого типа: а) первая итерация, б) вторая итерация.
Второй метод- это удаление элементов определенного размера из исходной фигуры, для получения нужной формы.
Вернемся к ранее рассмотренной кривой Коха, в данном методе будет рассматриваться “снежинка” Коха, принцип построения производится следующим образом:
Последовательные этапы построения снежинки Коха изображены на рис.7.
Все итерации располагаются в окружности конечного радиуса 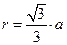 , где а - сторона первоначального треугольника.
, где а - сторона первоначального треугольника.

Рис.7. Снежинка Коха, первые 4 итерации.
Далее рассмотрим решето Серпинского. Процесс формирования такого фрактала показан на рис.8, на первом шаге состоит в удалении из исходного треугольника центрального треугольного сегмента с вдвое меньшей высотой. В образующихся новых треугольниках на втором шаге снова удаляют центральные части, и далее последовательно повторяют данную процедуру требуемое количество раз.

Рис.8. Решето Серпинского, первые 4 итерации.
Еще одно представление Серпинского - это ковер, который формируется по тому же принципу, что и решето. Из исходного квадрата, вырезается квадрат вдвое меньшего размера, и так далее повторяя это столько раз сколько необходимо. Ковер Серпинского представлен на рис.9.

Рис.9. Ковер Серпинского, первые 4 итерации.
Далее мы рассмотрим их подробнее.
1.4. Особенности проектирования и разработки ФА.
2. Техническая часть.
2.1. Анализ структур ФА.
Сравнение антенн
2.2. Классификация ФА.
Данные антенны можно классифицировать следующим образом:
1) По форме:
-кривые;
-ломанные;
-меандры;
-петли;
-решетки;
-ковры и так далее.
2) По полосе пропускания:
-узкополосные;
-широкополосные.
3) По виду поляризации:
-с вертикальной;
-с горизонтальной.
4) По диапазону волн:
-КВ;
-УКВ.
5) По диапазону частот:
-ВЧ;
-ОВЧ;
-УВЧ;
-СВЧ (частично).
6) По технологии изготовления:
-проволочные;
-при помощи напыления;
-печатные;
-фототравление.
7) По конструкции:
-антенны;
-антенные решетки;
-рамочные антенны.
И так формы ФА очень разнообразны рассмотрим некоторые из них:
1)
3. Моделирование ФА.
Для моделирования использовали программное обеспечение MMANA версии 3.0.
Данная программа позволяет выполнить следующее:
· Рассматривать множество антенн.
· Расчет диаграммы направленности (ДН) антенн в вертикальной и горизонтальной плоскостях.
· Сравнение результатов моделирования нескольких разных антенн (ДН и основные характеристики).
· Оптимизировать антенну, гибко настраивая цели оптимизации: Zвх, КСВ, усиление, F/B, минимум вертикального угла излучения, причем предельно наглядно – движками указывается важность для вас того или иного параметра.
· Строить множество разнообразных графиков: Zвх, КСВ, усиления, отношения излучений вперед/назад (F/B), включая показ зависимости ДН от частоты. Автоматически рассчитывать несколько типов согласующих устройств (СУ), возможность включать и выключать их при построении графиков.
· Рассчитывать катушки, контура, СУ на LС элементах, СУ на отрезках длинных линий (несколько видов), индуктивности и емкости, выполненные из отрезков коаксиального кабеля.
4. Перспективные направления.
5.Разработка рекомендаций по применению ФА.
Заключение.
В заключении хотелось бы скачать, что прогресс не стоит на месте.
Фрактальные антенны вскоре зарекомендуют себя в системах радиосвязи как основные приемо-передающие антенны, ведь они имеют достоинства перед стандартными антенными.
Приложение.
Список использованной литературы.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)