
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторная работа № 1. Построение прогнозов
|
|
По 15 предприятиям отрасли (табл. 1.1) известны: 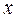 – объем произведенной продукции (тыс. ед.) и
– объем произведенной продукции (тыс. ед.) и 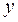 – затраты на выпуск этой продукции (тыс. ден. ед.). Необходимо:
– затраты на выпуск этой продукции (тыс. ден. ед.). Необходимо:
1) определить зависимость 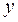 от
от 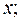
2) построить корреляционные поля и график уравнения линейной регрессии 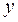 на
на 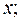
3) сделать вывод о качестве модели и рассчитать прогнозное значение 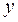 при прогнозном значении
при прогнозном значении 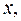 составляющем 107% от среднего уровня.
составляющем 107% от среднего уровня.
Таблица 1.1
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| x | 2, 7 | 1, 5 | 8, 2 | 4, 5 | 3, 3 | 5, 8 | 3, 0 | 7, 1 | 1, 2 | 10, 4 | 4, 9 | 5, 2 | 11, 5 | 9, 4 | 6, 5 |
| y |
Решение:
1) В Excel составим вспомогательную таблицу 1.2.
Таблица 1.2
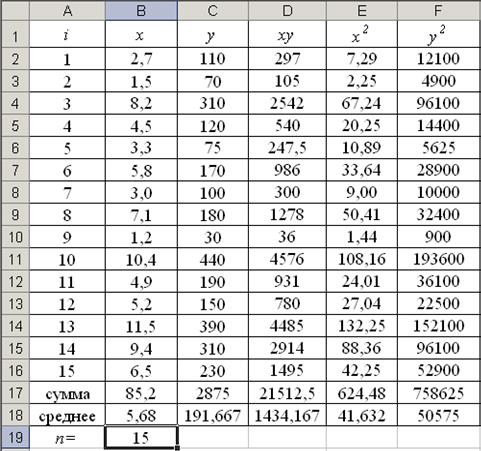
Вычислим количество измерений 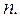 Для этого в ячейку В19 поместим = СЧЁТ(A2: A16).
Для этого в ячейку В19 поместим = СЧЁТ(A2: A16).
С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех 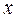 (ячейка В17) и
(ячейка В17) и 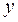 (ячейка С17).
(ячейка С17).
Вычислим выборочные средние: 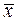 =5, 68;
=5, 68; 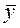 =191, 67. Таким образом, средний объем произведенной продукции по 15 предприятиям отрасли составляет 5, 68 тыс. ед., а средние затраты на выпуск этой продукции – 191, 67 тыс. ден. ед.
=191, 67. Таким образом, средний объем произведенной продукции по 15 предприятиям отрасли составляет 5, 68 тыс. ед., а средние затраты на выпуск этой продукции – 191, 67 тыс. ден. ед.
Заполним столбцы D, E, F. Например, в ячейку D2 поместим = B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2 и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.
Для вычисления в ыборочной ковариации между 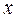 и
и 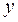 используем формулу
используем формулу 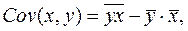 т.е. в ячейку B21 поместим = D18-B18*C18 и получим 345, 5 (рис. 1.1).
т.е. в ячейку B21 поместим = D18-B18*C18 и получим 345, 5 (рис. 1.1).
Выборочную дисперсию для 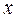 найдем по формуле
найдем по формуле 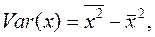 т.е. в ячейку B22 поместим = E18-B18*B18 и получим 9, 37 (рис. 1.1). Аналогично определяем
т.е. в ячейку B22 поместим = E18-B18*B18 и получим 9, 37 (рис. 1.1). Аналогично определяем 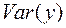 =13838, 89.
=13838, 89.
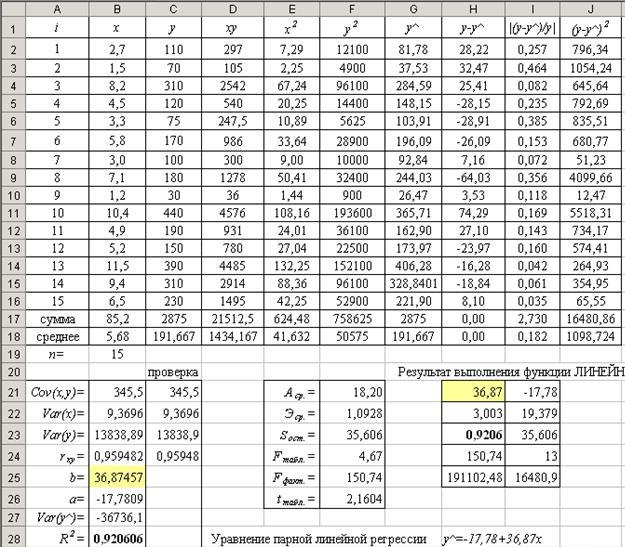
Рис. 1.1. Решение примера 1.1 в Excel
Выборочный коэффициент корреляции 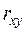 =0, 96 очень высокий, что указывает на прямую и весьма сильную связь между
=0, 96 очень высокий, что указывает на прямую и весьма сильную связь между 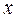 и
и 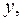 т.е. с ростом объема произведенной продукции
т.е. с ростом объема произведенной продукции 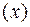 увеличиваются затраты на выпуск этой продукции
увеличиваются затраты на выпуск этой продукции 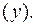
Выборочный коэффициент линейной регрессии 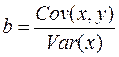 =36, 87; параметр
=36, 87; параметр 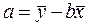 =-17, 78. Значит, уравнение парной линейной регрессии имеет вид
=-17, 78. Значит, уравнение парной линейной регрессии имеет вид 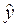 =-17, 78+36, 87
=-17, 78+36, 87 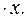
Коэффициент 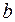 показывает, что при увеличении объема произведенной продукции
показывает, что при увеличении объема произведенной продукции 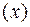 на 1 тыс. ед. затраты на выпуск этой продукции
на 1 тыс. ед. затраты на выпуск этой продукции 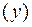 в среднем увеличатся на 36, 87 тыс. ден. ед.
в среднем увеличатся на 36, 87 тыс. ден. ед.
2) Подставляя в найденное уравнение регрессии фактические значения 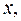 определим теоретические (расчетные) значения
определим теоретические (расчетные) значения 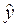 в столбце G.
в столбце G.
С помощью Мастера диаграмм строим корреляционные поля (выделяя столбцы со значениями 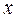 и
и 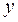 ) и уравнение линейной регрессии (выделяя столбцы со значениями
) и уравнение линейной регрессии (выделяя столбцы со значениями 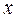 и
и 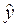 ). Выбираем тип диаграммы – Точечная и, следуя рекомендациям Мастера диаграмм, вводим нужные параметры (название, подписи к осям, легенду и т.п.). В результате получим рис. 1.2.
). Выбираем тип диаграммы – Точечная и, следуя рекомендациям Мастера диаграмм, вводим нужные параметры (название, подписи к осям, легенду и т.п.). В результате получим рис. 1.2.
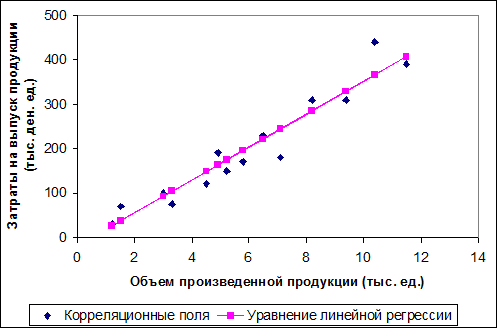
Рис. 1.2. График зависимости объема произведенной продукции
от теоретических и фактических затрат на выпуск этой продукции
3) Для оценки качества построенной модели регрессии вычислим:
• коэффициент детерминации 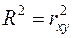 =0, 92, который показывает, что изменение затрат на выпуск продукции
=0, 92, который показывает, что изменение затрат на выпуск продукции 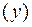 на 92% объясняется изменением объема произведенной продукции
на 92% объясняется изменением объема произведенной продукции 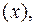 а 8% приходится на долю неучтенных в модели факторов, что указывает на качественность построенной регрессионной модели;
а 8% приходится на долю неучтенных в модели факторов, что указывает на качественность построенной регрессионной модели;
• среднюю ошибку аппроксимации. Для этого в столбце H вычислим 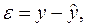 а в столбце I – выражение
а в столбце I – выражение 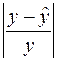 (рис. 1.1). При умножении средне1го значения (ячейка I18) на 100% получим
(рис. 1.1). При умножении средне1го значения (ячейка I18) на 100% получим 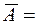 18, 2%. Следовательно, в среднем теоретические значения
18, 2%. Следовательно, в среднем теоретические значения 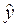 отклоняются от фактических
отклоняются от фактических 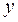 на 18, 2%.
на 18, 2%.
С помощью 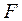 -критерия Фишераоценим значимость уравнения регрессии в целом:
-критерия Фишераоценим значимость уравнения регрессии в целом: 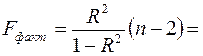 150, 74.
150, 74.
На уровне значимости 0, 05 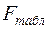 =4, 67 определяем по таблице
=4, 67 определяем по таблице 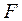 -критерия Фишера (таблица 1 приложения) либо с помощью встроенной статистической функции FРАСПОБР (рис. 1.3).
-критерия Фишера (таблица 1 приложения) либо с помощью встроенной статистической функции FРАСПОБР (рис. 1.3).
Так как 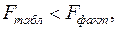 то уравнение регрессии значимо при
то уравнение регрессии значимо при 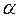 =0, 05.
=0, 05.
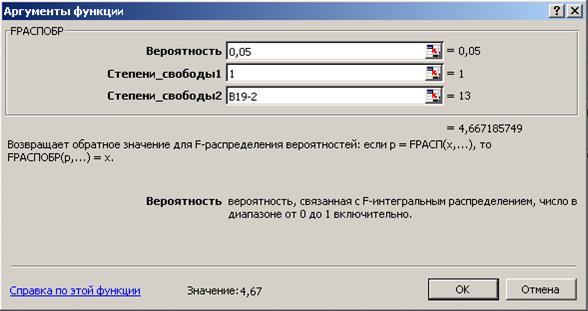
Рис. 1.3. Диалоговое окно функции FРАСПОБР
Средний коэффициент эластичности 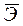 =1, 09 показывает, что с ростом объема произведенной продукции на 1% затраты на выпуск этой продукции в среднем по совокупности возрастут на 1, 09%.
=1, 09 показывает, что с ростом объема произведенной продукции на 1% затраты на выпуск этой продукции в среднем по совокупности возрастут на 1, 09%.
Рассчитаем прогнозное значение 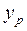 путем подстановки в уравнение регрессии
путем подстановки в уравнение регрессии 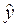 =-17, 78+36, 87
=-17, 78+36, 87 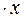 прогнозного значения фактора
прогнозного значения фактора 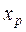 =
= 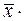 1, 07=6, 08. Получим
1, 07=6, 08. Получим 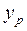 =206, 33. Следовательно, при выпуске продукции в количестве 6, 08 тыс. ед. затраты на производство этой продукции составят 206, 33 тыс. ден. ед.
=206, 33. Следовательно, при выпуске продукции в количестве 6, 08 тыс. ед. затраты на производство этой продукции составят 206, 33 тыс. ден. ед.
Найдем 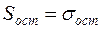 =35, 606 поместив в ячейку F23 = КОРЕНЬ(J17/(B19-2)).
=35, 606 поместив в ячейку F23 = КОРЕНЬ(J17/(B19-2)).
Средняя стандартная ошибка прогноза:
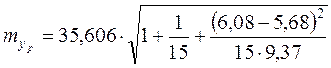 =36, 79.
=36, 79.
На уровне значимости 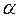 =0, 05 либо по таблице
=0, 05 либо по таблице 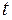 - критерия Стьюдента (таблица 2 приложения) либо с помощью встроенной статистической функции СТЬЮДРАСПОБР определим
- критерия Стьюдента (таблица 2 приложения) либо с помощью встроенной статистической функции СТЬЮДРАСПОБР определим  =2, 1604 и вычислим предельную ошибку прогноза, которая в 95% случаев не будет превышать
=2, 1604 и вычислим предельную ошибку прогноза, которая в 95% случаев не будет превышать 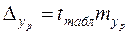 =79, 48.
=79, 48.
Доверительный интервал прогноза:
206, 33-79, 48 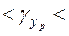 206, 33+79, 48 или 126, 85
206, 33+79, 48 или 126, 85 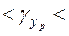 285, 81.
285, 81.
Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0, 05=0, 95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 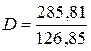 =2, 25 раза. Это произошло за счет малого объема наблюдений.
=2, 25 раза. Это произошло за счет малого объема наблюдений.
Решение эконометрических задач можно упростить, используя встроенные функции. Активизируем Мастер функций любым из способов:
• в главном меню выбрать Вставка / Функция;
• на панели инструментов Стандартная щелкнуть по кнопке  Вставка функции.
Вставка функции.
Для вычисления выборочных средних используем функцию СРЗНАЧ(число1: числоN) из категории Статистические.
Выборочная ковариация между 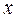 и
и 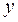 находится с помощью функции КОВАР(массив X; массив Y) из категории Статистические.
находится с помощью функции КОВАР(массив X; массив Y) из категории Статистические.
Выборочные дисперсии определяются статистической функцией ДИСПР(число1: числоN).
Выборочный коэффициент корреляции между 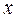 и
и 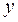 вычисляется с помощью статистической функции КОРРЕЛ(массив X; массив Y).
вычисляется с помощью статистической функции КОРРЕЛ(массив X; массив Y).
Параметры линейной регрессии 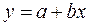 в Excel можно определить несколькими способами.
в Excel можно определить несколькими способами.
1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:
1. Выделить область пустых ячеек 5x2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1x2 – для получения только коэффициентов регрессии.
2. С помощью Мастера функций среди Статистических выбрать функцию ЛИНЕЙН и заполнить ее аргументы (рис. 1.4):
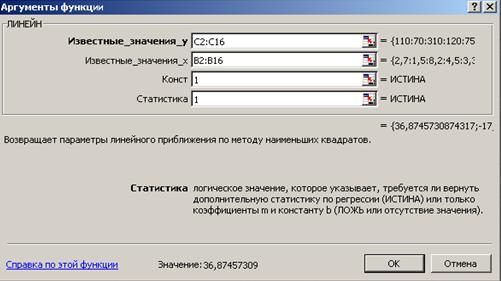
Рис. 1.4. Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_y – диапазон, содержащий данные результативного признака Y;
Известные_значения_x – диапазон, содержащий данные объясняющего признака X;
Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;
Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.
3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу < F2>, а затем – на комбинацию клавиш < CTRL> + < SHIFT> + < ENTER>.
Дополнительная регрессионная статистика будет выведена в виде (табл. 1.3):
Таблица 1.3
Значение коэффициента 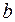
| Значение коэффициента 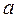
|
Среднеквадратическое отклонение 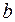
| Среднеквадратическое отклонение 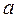
|
Коэффициент детерминации 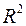
| Среднеквадратическое отклонение 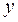
|
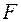 -статистика -статистика 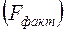
| Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
В результате применения функции ЛИНЕЙН получим:
| 36, 87 | -17, 78 |
| 3, 003 | 19, 379 |
| 0, 9206 | 35, 606 |
| 150, 74 | |
| 191102, 48 | 16480, 9 |
(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:
1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню нужно выбрать Сервис / Настройки и напротив Пакета анализа установить флажок.
2. Выбрать в главном меню Сервис / Анализ данных / Регрессия и заполнить диалоговое окно (рис. 1.5):
Входной интервал Y – диапазон, содержащий данные результативного признака Y;
Входной интервал X – диапазон, содержащий данные объясняющего признака X;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне. В результате получим итоги как на рис. 1.6.
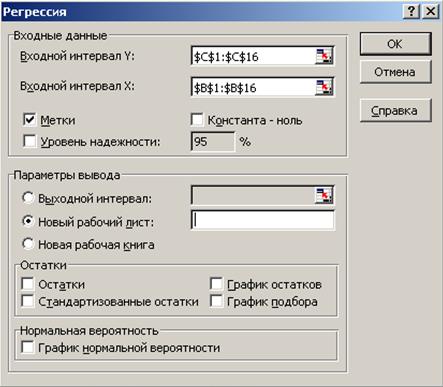
Рис. 1.5. Диалоговое окно ввода параметров инструмента Регрессии
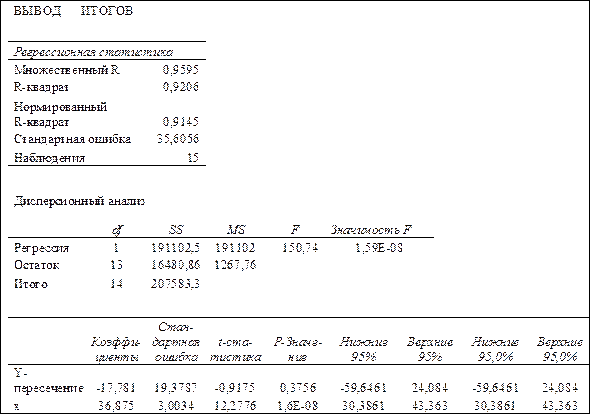
Рис. 1.6. Результаты применения инструмента Регрессия
В Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1. Необходимо выделить область построения диаграммы и в главном меню выбрать Диаграмма / Добавить линию тренда.
2. В появившемся диалоговом окне (рис. 1.7) выбрать вид линии тренда и задать соответствующие параметры.
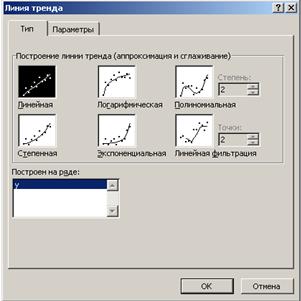
Рис. 1.7. Диалоговое окно типов линии тренда
Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.
Выбираем Линейная для построения уравнения линейной регрессии.
В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину 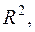 установив соответствующие флажки на закладке Параметры (рис. 1.8).
установив соответствующие флажки на закладке Параметры (рис. 1.8).
В результате получим линейный тренд (рис. 1.9).
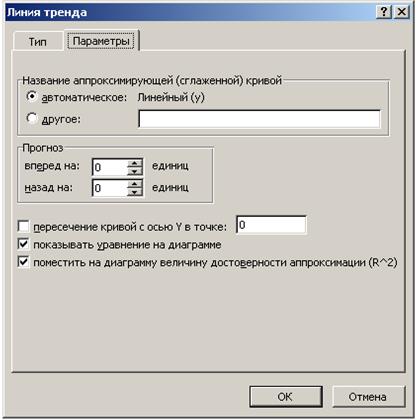
Рис. 1.8. Диалоговое окно параметров линии тренда
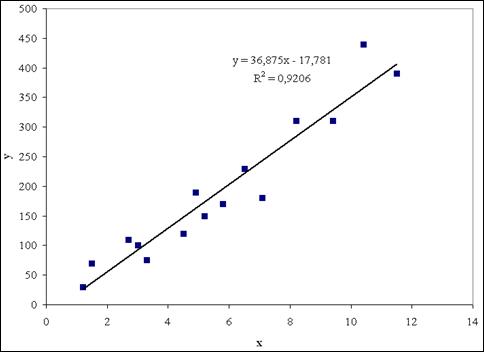
Рис. 1.9. Линейный тренд
Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения 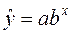 с применением выбранной в Excel статистической функции ЛГРФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.
с применением выбранной в Excel статистической функции ЛГРФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.
|